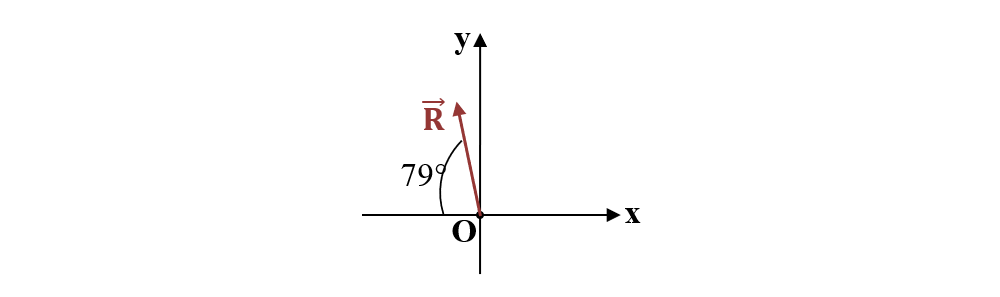
V.2.3. Compunerea analitică a forțelor.
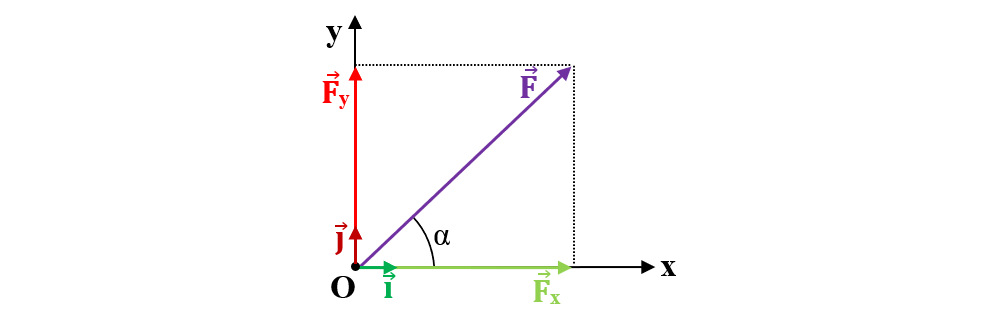
Compunerea analitică a forțelor se realizează prin proiecția unei forțe pe două direcții reciproc perpendiculare. Astfel, din vârful vectorului dat se duc perpendiculare pe cele două direcții Ox și Oy.
Scriem ecuația vectorială:

Scriem ecuația scalară:
F2 = Fx2 + Fy2 (teorema lui Pitagora).

🔓 Problemă rezolvată
1. Să se determine rezultanta sistemului următor de forțe știind că F1 = 300 N, F2 = 200 N, F3 = 100 N, F4 = 400 N, F5 = 500 N. Află și unghiul θ făcut de rezultantă cu axa Ox și apoi reprezintă grafic forța rezultantă.
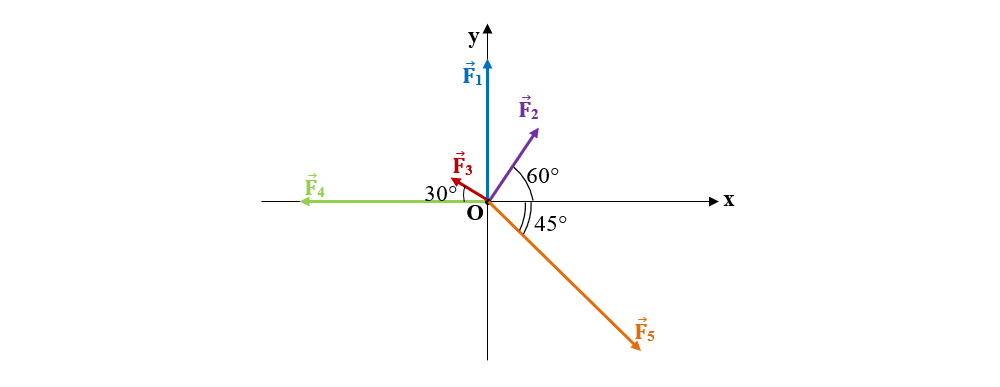
Rezolvare :
-
Ducem proiecțiile ortogonale ale fiecărei forțe pe axele Ox și Oy și calculăm aceste proiecții.
-
Proiecțiile ortogonale ale forței F1 pe axele Ox și Oy
F1x = F1 ∙ cos α = 300 ∙ cos 90° = 0
F1y = F1 ∙ sin α = 300 ∙ sin 90° = 300 N -
Proiecțiile ortogonale ale forței F2 pe axele Ox și Oy
F2x = F2 ∙ cos α = 200 ∙ cos 60° = 100 N
F2y = F2 ∙ sin α = 200 ∙ sin 60° = 173,2 N -
Proiecțiile ortogonale ale forței F3 pe axele Ox și Oy
F3x = -F3 ∙ cos α = -100 ∙ cos 30° = -86,6 N
F3y = F3 ∙ sin α = 100 ∙ sin 30° = 50 N -
Proiecțiile ortogonale ale forței F4 pe axele Ox și Oy
F4x = -F4 ∙ cos α = -400 ∙ cos 0° = -400 N
F4y = F4 ∙ sin α = 400 ∙ sin 0° = 0 -
Proiecțiile ortogonale ale forței F5 pe axele Ox și Oy
F5x = F5 ∙ cos α = 500 ∙ cos 45° = 353,5 N
F5y = -F5 ∙ sin α = -500 ∙ sin 45° = -353,5 N -
Calculăm rezultanta tuturor proiecțiilor pe axa Ox și cea pe axa Oy, prin însumare algebrică
Rx = ∑Fix = 0 + 100 N - 86,6 N - 400 N + 353,5 N = -33,1 N
Ry = ∑Fjy = 300 N + 173,2 N + 50 N + 0 – 353,5 N = 169,9 N -
Calculăm rezultanta lui Rx și Ry:
R2 = Rx2+ Ry2 = (-33,1)2 + (169,9)2 = 1095,61 + 28866,01 = 29961,62

- Unghiul θ făcut de rezultantă cu axa Ox se calculează cu următoarea formulă :