V.3.1. Momentul unei forțe în raport cu un punct.

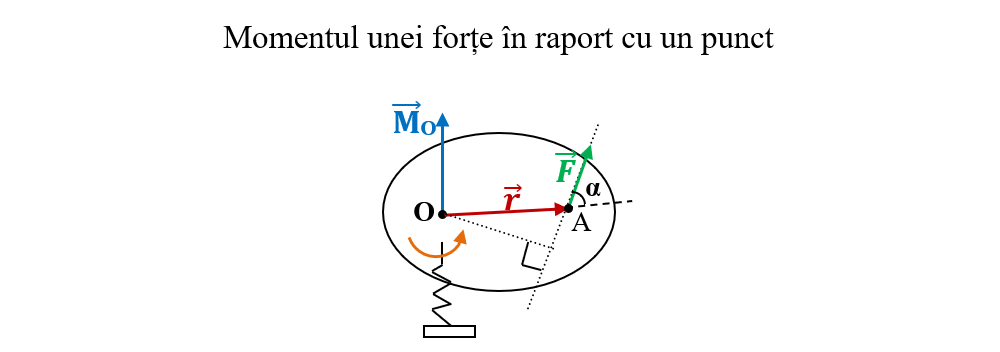
Vectorul momentul unei forțe în raport cu un punct (pol) se caracterizează prin:

MO = F ∙ r ∙ sin α = F ∙ d
d = r ∙ sin α – este brațul forței, adică distanța (perpendiculara) de la axul de rotație (O) până la direcția (suportul) forței.
Unitate de măsură în S.I:
[MF]SI = [F]SI ∙[d]SI = N ∙ m
🔦 Observație
Produsul N ∙ m nu trebuie înlocuit cu joule, deoarece MO = F ∙ d nu reprezintă un lucru mecanic (d este brațul forței și nu deplasarea punctului de aplicație a forței).
În funcție de valoarea momentului unei forțe putem stabili dacă forța rotește un corp. Avem două cazuri :
I. Dacă MO = 0, atunci forța aplicată nu rotește corpul.
Momentul unei forței este zero (MO = 0) când d = 0 (când punctul O se află pe suportul forței și nu putem duce perpendiculară din axul de rotație pe direcția forței).

II. Dacă MO > 0, atunci forța aplicată rotește corpul.
