V.5.1. Condițiile de echilibru pentru un solid rigid.

• V.5.1.1. Condiția echilibrului de translație a solidului rigid.
• V.5.1.2. Condiția echilibrului de rotație a solidului rigid.

V.5.1.1. Condiția echilibrului de translație a solidului rigid.

Condiția necesară și suficientă pentru ca o particulă materială să fie în echilibru de translație este ca rezultanta forțelor ce acționează asupra acesteia să fie nulă.

🔓 Problemă rezolvată

1. Un corp cu greutatea de 300 N se mișcă uniform pe o suprafață orizontală sub acțiunea a două forțe: F₁ = 100 N care face un unghi α₁ = 60° cu orizontala și F₂ = 200 N care face un unghi α₂ = 30° cu orizontala.

a) Să se reprezinte forțele ce acționează asupra corpului.

b) Sensul mișcării corpului.

c) Ce valoare trebuie să aibă forța de frecare și reacțiunea normală ca acest corp să fie în echilibru de translație ?

Rezolvare:

a)

b) Pentru a afla sensul mișcării se compară componentele forțelor de tracțiune pe axa de mișcare, Ox.

F_x1 = F₁ ∙ cos α₁ = F₁ ∙ cos 60° = 100 N ∙ 0,5 = 50 N

F_x2 = F₂ ∙ cos α₂ = F₂ ∙ cos 30° = 200 N ∙ 0,86 = 172 N

Deoarece F_x2 > F_x1, înseamnă că mișcarea corpului se face în sensul forței F_x2, adică spre stânga.

c) Un corp este în echilibru de translație atunci când forța rezultantă ce acționează asupra lui este egală cu zero.

Pe axa Ox punem condiția ca forța rezultantă să fie 0.
| F_x1 + F_f | = | F_x2 |
| 50 N + F_f | = 172 N
F_f = 122 N

Pe axa Oy punem condiția ca forța rezultantă să fie 0. Atunci vom avea următoarea egalitate :
| F_y1 + N + F_y2 | = | G |
F_y1 = F₁ ∙ sin α1 = F₁ ∙ sin 60° = 100 N ∙ 0,86 = 86 N
F_y2 = F₂ ∙ sin α2 = F₂ ∙ sin 30° = 200 N ∙ 0,5 = 100 N
| 86 N + N + 100 N | = 300 N
N = 114 N

V.5.1.2. Condiția echilibrului de rotație a solidului rigid.

👀 Experiment: Echilibrul de rotaţie

Materiale necesare:
Ață cu cârlig, disc cu perforații, suport, cârlig cu mase marcate.

Descrierea experimentului:

• Agață de una dintre perforațiile discului din dreapta un cârlig cu discuri marcate și observă sensul în care se rotește discul cu perforații.
• Agață de o altă perforație a discului din stânga (să aibă același braț cu cel din dreapta) și pune mase pe cârlig până când discul nu se mai rotește.
• Găsește condiția de echilibru de rotație pentru acest caz.

  Greutatea maselor marcate din partea stângă este egală cu greutatea maselor din partea dreaptă.

Concluzia experimentului:
Se constată că modulele momentelor forțelor | M₁ | = | F₁ • b₁ | și | M₂ | = | F₂ • b₂ | față de centrul de rotație sunt egale atunci când discul se află în echilibru de rotație: | M₁ | = | M₂ |.

Un solid rigid este în echilibru de rotaţie atunci când momentul rezultant al forțelor aplicate solidului este nul.

Dacă forțele care acționează asupra unui solid rigid sunt coplanare în planul xOy, atunci condițiile de echilibru care trebuie îndeplinite simultan pentru translație și rotație, sunt:

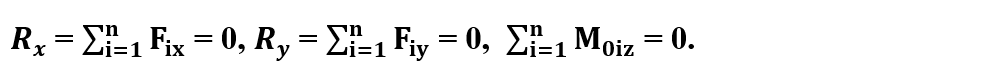
🔦 Observație

Un corp este în echilibru de rotaţie atunci când corpul** nu se roteşte** sau când are o mişcare de rotaţie uniformă.