V.2.4. Compunerea forțelor paralele.
- V.2.4.1. Compunerea forțelor paralele de același sens.
- V.2.4.2. Compunerea forțelor paralele de sens opus.
V.2.4.1. Compunerea forțelor paralele de același sens.
Forțele paralele sunt forțele care au dreptele suport pe aceeași direcție.
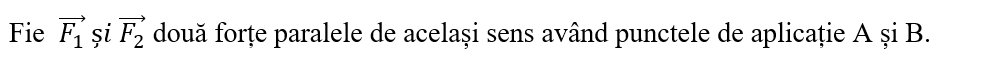
Mărimea rezultantei este egală cu suma algebrică a mărimilor celor două forțe, având același sens cu ele.
R = F1 + F2

Determinarea punctului de aplicație a rezultantei se face prin metodă grafică urmând pașii următori:

- Din asemănarea triunghiurilor ΔCBBʹ~ ΔCAAʹ se obține legea pârghiilor :

👀 Experiment: Compunerea forțelor paralele
Materiale necesare:
Un scripete fix, un suport, 3 cârlige cu mase marcate, fir inextensibil, vergea gradată.
Descrierea experimentului:
- Se realizează următorul montaj:
-
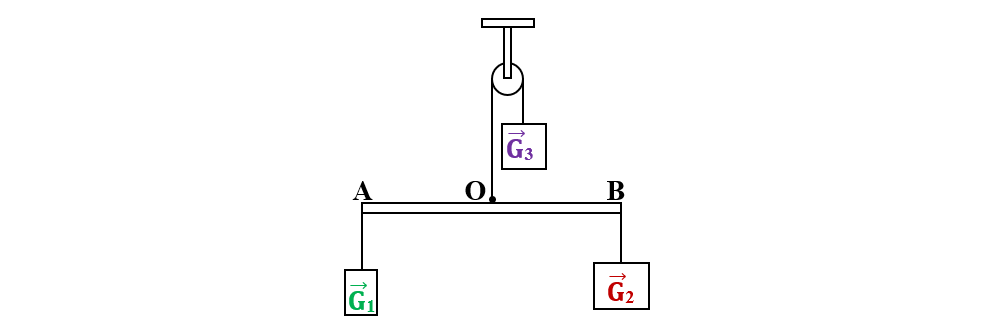
De un capăt al firului trecut peste scripetele fix se pun un cârlig cu mase marcate.
-
Pe vergeaua gradată se suspendă de o parte și de alta cârlige cu mase marcate până când sistemul este în echilibru. Se măsoară forța rezultantă practică, Rp = G3.
-
Se calculează forța rezultantă teoretică, Rt.
Rt = F1 + F2 -
Se compară cele două rezultante.
-
Dacă nu coincid cele două valori, Rp = Rt, se notează sursele de erori de măsură (măsurarea forțelor etc.).
-
Se repetă măsurătorile cu alte valori ale greutăților G1 și G2 și cu alte distanțe de la centrul pârghiei la punctele de aplicație ale celor două forțe paralele, pe care le trecem în tabelul de date:

- Se măsoară distanțele AO și BO și se verifică legea pârghiei pentru fiecare determinare.

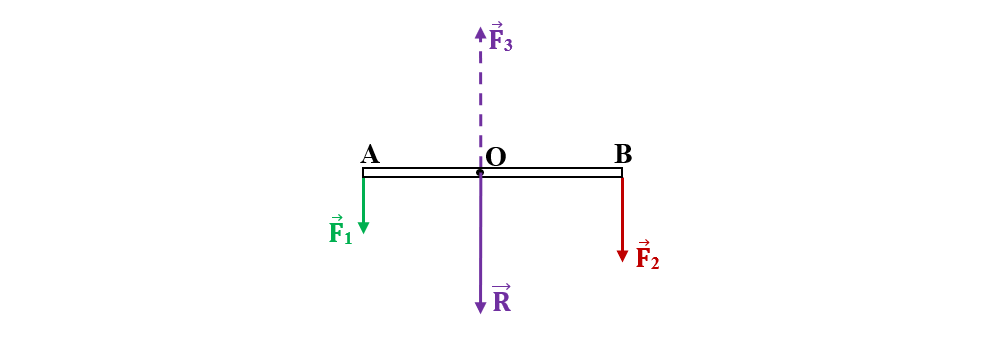
V.2.4.2. Compunerea forțelor paralele de sens opus.
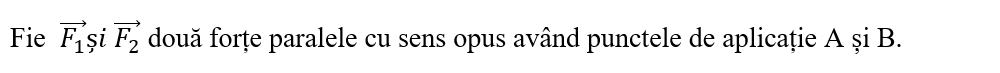
Considerăm F1 > F2
Mărimea rezultantei este egală cu suma algebrică a mărimilor celor două forțe, având sensul forței cu modulul mai mare.
R = F1 - F2
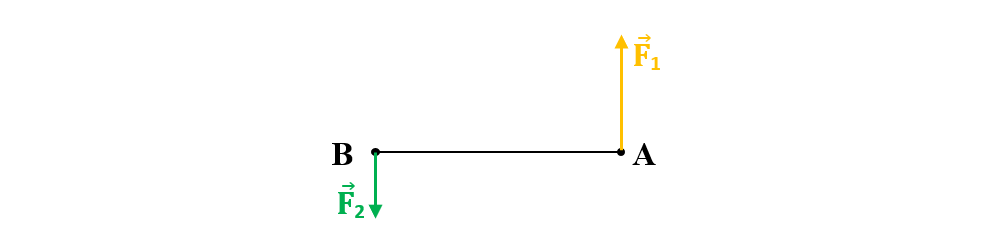
Determinarea punctului de aplicație a rezultantei se face prin metodă grafică, urmând pașii următori:

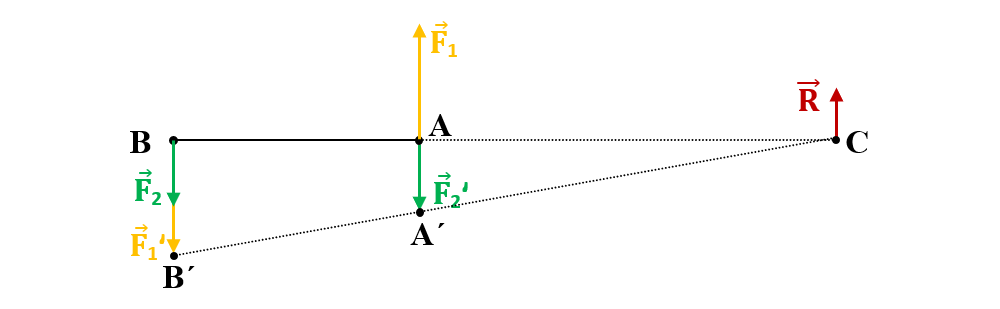
- Din asemănarea triunghiurilor ΔCBBʹ~ ΔCAAʹ se obține legea pârghiilor:
