IV.5.3. Curba lui Koch
Curba lui Koch a fost construită de către acesta în 1904. Karl Weierstrass a demonstrat primul existența unei astfel de curbe în 1872. Acest fractal geometric determinist are ca inițiator un segment de dreaptă.
- Prima iterație constă în împărțirea acestui segment (de culoare verde) în trei părți egale, la care segmentul din mijloc se înlocuiește cu cele două laturi ale unui triunghi echilateral de aceleași lungimi ca și lungimea segmentului (cele 2 segmente roșii din mijlocul figurii).
Rezultatul primei iterații

- După prima iterație, dimensiunea Hausdorff este:

- Pentru a doua iterație repetăm operația, luând fiecare din cele 4 segmente rezultate, împărțindu-le în 3 părți egale și înlocuind fiecare din segmentele din mijloc cu 2 laturi ale unui triunghi echilateral (segmentele roșii din partea de jos a figurii).

După a doua iterație, dimensiunea Hausdorff este:
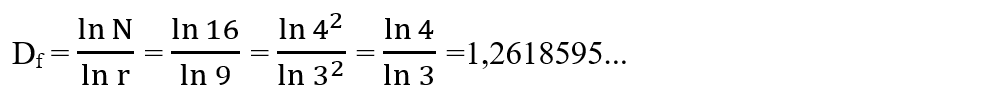
- După a treia iterație:

- După n iterații:
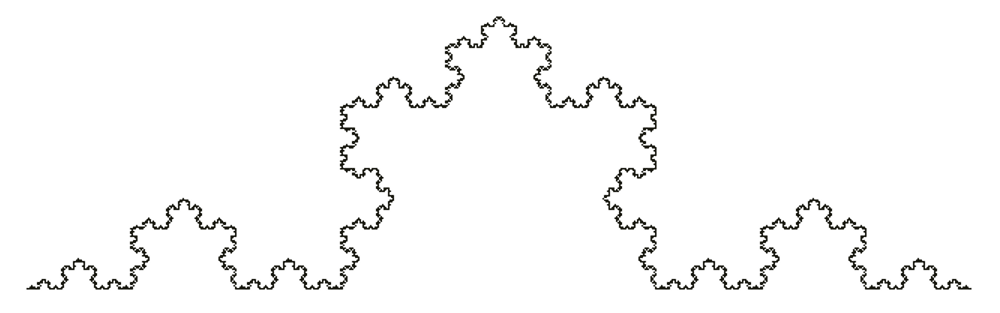
La fiecare iterație, perimetrul curbei crește cu patru treimi și după n iterații este infinit.
Fractalul lui Koch este o curbă continuă și infinită, care nu are tangente în nici un punct al său. De asemenea, lungimea curbei între oricare două puncte ale curbei este infinită, existând o copie a curbei Koch între oricare două puncte ale sale.
🔦 Observație
Aria suprafeței curbei lui Koch este zero. Cum noi știm că o suprafață este bidimensională, vom spune că aceasta nu este nici o linie (cu dimensiunea 1), nici o suprafață (cu dimensiunea 2), ci este un fractal cu dimensiune între 1 și 2 (Df = 1,2618595...).
Dacă se construiesc trei curbe Koch pe exteriorul laturilor unui triunghi echilateral, se obține o curbă simplă și închisă, numită curba Jordan sau insula lui Koch.
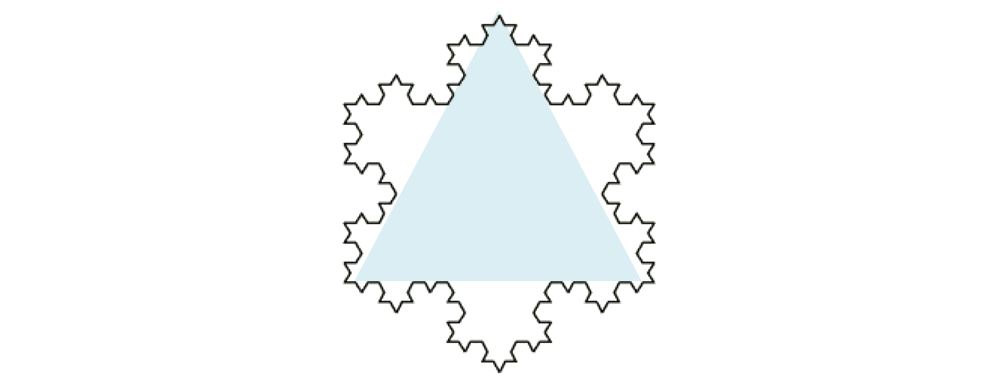
Insula lui Koch este un exemplu de domeniu plan cu arie finită, mărginit de o curbă Jordan cu lungime infinită.
Curba lui Koch descrie geometriile proceselor de cristalizare ale fulgilor de zăpadă.