IV.5.11. Aplicațiile fractalilor

Dintotdeauna oamenii de știință au încercat să cunoască lumea reală pentru a o putea controla și anticipa evenimentele viitoare. Din păcate, natura nu poate fi descrisă numai prin ecuații și legi care să-i prezică comportamentul pe termen lung. Acest lucru se întâmplă deoarece, formele și fenomenele naturale sunt preponderent neliniare și haotice.

Teoria haosului și fractalii sunt instrumente puternice în analizarea sistemelor neliniare ale lumii reale.

Un sistem dinamic și neliniar are o evoluție sensibilă la condițiile inițiale, fiind imposibil de controlat datorită unei mici schimbări neperiodice anterioare.

Teoria haosului și a fractalilor nu poate prezice exact momentul când un sistem va deveni haotic sub acțiunea atractorilor stranii (când va avea loc un cutremur, o revoltă a sindicaliștilor, scăderea acțiunilor la bursă etc.). Modelarea se realizează prin curbe fractale pentru a determina caracterul esențial al sistemului, deci pentru simulare și nu în scopuri predictive.

Graficele fractale ne ajută să înțelegem dinamica și evoluția în timp a fenomenelor naturale și sociale prin determinarea bazinului de atractori spre care tinde sistemul. Astfel, complexitatea fractalilor le permit acestora să modeleze și să simuleze sisteme dinamice din diferite domenii : biologie, fizică, chimie, geografie, hidrologie, meteorologie, geologie, economie, medicina, psihologie, astronomie, management etc.

Aplicațiile fractalilor:

• În economie, analiza pieței folosește graficele fractale. Piața are memorie atât pe termen scurt, cât și pe lung și de aceea este definită de trei atractori : cererea, oferta și structura fractală ce va induce haosul în sistem. Simularea tendinței prețurilor produselor de consum prezice cu exactitate cantitatea de variație din prețul produsului (lunar, anual etc.), dar nu poate indica prețul la o anumită dată. Evoluția prețului acțiunilor la bursă, a cursului valutar într-un anumit interval de timp este ușor de modelat cu ajutorul fractalilor.

• În management, teoria haosului este folosită pentru a realiza o serie de scenarii ale sistemului social studiat. Orice organizație socială este privită ca un sistem complex cu diferite nivele de stabilitate și haos. Un lider adevărat trebuie să fie conștient că evoluția relațiilor în orice comunitate este imposibil de prezis și că singura soluție este să acționeze prompt atunci când apar schimbări provocatoare în organizația condusă, pentru ca haosul local să nu devină un haos general, asemenea unei tornade.

• Grafica pe calculator este prima aplicaţie majoră a fractalilor, prin comprimarea unei imagini foarte mari în coduri foarte mici, mai puțin de un sfert din dimensiunea inițială a fișierului. Comprimarea fractală a imaginii este foarte utilă în multe domenii, ca de exemplu transmiterea în timp real a imaginilor video prin liniile telefonice normale.

• În diferite domenii științifice, geometria fractală de redare grafică pe calculator este folosită de oamenii de știință pentru a crea diferite structuri naturale. Fractali pot modela diferite forme din natură, cum ar fi nori, fulgii de zăpadă, cristalele, lanțurile montane, fulgerele, rețelele de râuri etc. Cutremurele, debitele râurilor sunt ușor de modelat cu ajutorul curbelor fractale.

• În biologie și medicină, analiza fractală este din ce în ce mai folosită la studierea sistemelor biologice, atât la scară macroscopică, cât și la scară microscopică. De exemplu, în corpul uman pot fi modelate cu ajutorul fractalilor ramificațiile vaselor de sânge, structura rinichiului, structura scheletului, plămânii, inima, sistemul nervos, ADN-ul etc. Se pot analiza neregularitățile care apar la granița dintre un țesut sănătos și o tumoare.

• În meteorologie, geometria fractală este folosită pentru a explica de ce vremea nu poate fi anticipată pe termen lung, ci numai pentru câteva zile.

• În astronomie, pe termen scurt (zeci sau sute de ani) poate fi anticipată traiectoria corpurilor cerești, pe baza legii gravitaționale a lui Newton. Pe termen foarte mare (milioane de ani) poate apărea o comportare neliniară în dinamica orbitei corpului respectiv.

• Arta fractală este o formă de artă algoritmică ce folosește fractalii și reprezentările computerizate pentru a genera imagini, animații, muzică, efecte speciale în producțiile cinematografice, diverse arhitecturi moderne etc.

Exemple:

• Un fractal care modelează structura unui profil muntos:

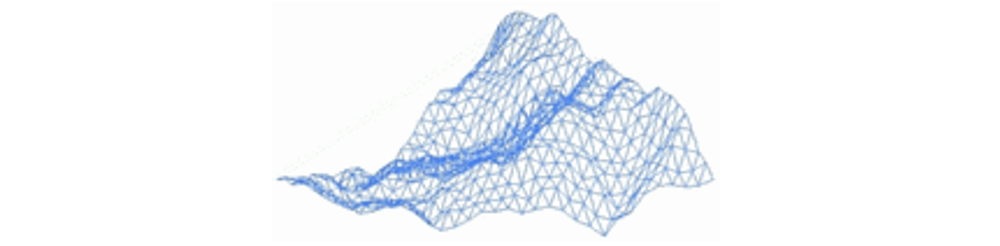
• Degradarea unui bloc acrilic sub acțiunea unui curent de înaltă tensiune produce un fractal figură Lichtenberg.

• Un grup format prin agregare limitată de difuzie, dezvoltat dintr-o soluție de sulfat de cupru într-o celulă electrolitică.

• Obținerea unor ace de amalgam de argint în reacția dintre mercur și azotat de argint.

• Fractal Sterling 2