IV.5.2. Covorul lui Sierpinski
Covorul lui Sierpinski (magia puterilor lui 8) este un fractal geometric determinist care are drept inițiator un pătrat. Laturile pătratului se împart în 3, deci factorul de scară este r = 3. Din cele 9 pătrate obținute se elimină pătratul din mijloc, păstrându-se cele 8 copii (N = 8).
- După prima iterație, dimensiunea Hausdorff este:


- Pentru a realiza a doua iterație, figura obținută după prima iterație se multiplică de 9 ori, iar cea din mijloc se înnegrește. După a doua iterație se obțin 64 de copii (N = 64), r = 9 și dimensiunea Hausdorff este:
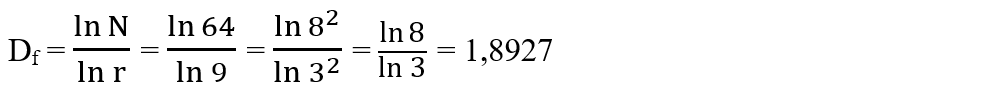

- Pentru a realiza a treia iterație, figura obținută după a doua iterație se multiplică de 9 ori, iar cea din mijloc se înnegrește. După a treia iterație se obțin 4096 de copii (N = 642), r = 81 și dimensiunea Hausdorff este:
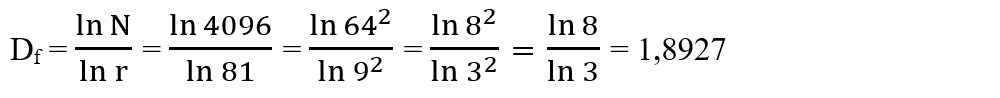
🔦 Observație
Aria pătratului lui Sierpinski este nulă, iar lungimea sa este infinită.
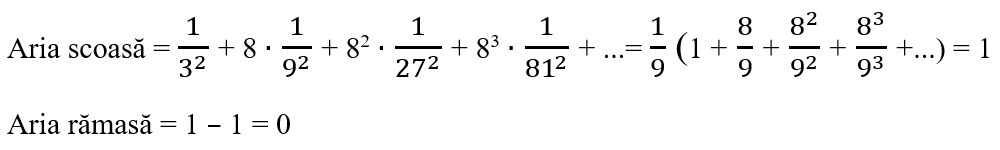

- După n iterații, dimensiunea Hausdorff este:

🔦 Observație
Având la bază un pătrat, covorul lui Sierpinski are ca dimensiune euclidiană 2, mai mare decât dimensiunea Hausdorff.