Skip to main content

II.2.4.1. Overview

📚

The volume of a body is the place occupied by a body in space.

📚

Characterization of the volume as physical parameter:



Another measurement unit for volume (capacity) is the liter: 1 L = 1dm3.

Cubic meter multiples and submultiples are also used.

🔦 Remark

Here is how to perform these transformations from multiples and submultiples of m3 into m3:

  • Write the numerical value and open a parenthesis, in which the value of the given multiple or submultiple is written, close the parenthesis and raise everything to the respective power, ie to the cube (3rd power).
  • Copy the given value again and multiply by the values in parentheses raised to the third power.
  • The corresponding mathematical calculations are made and the result is given.
📋

Examples of transformations from multiples and sub-multiples of m3 or liter (L) into m3:

📋

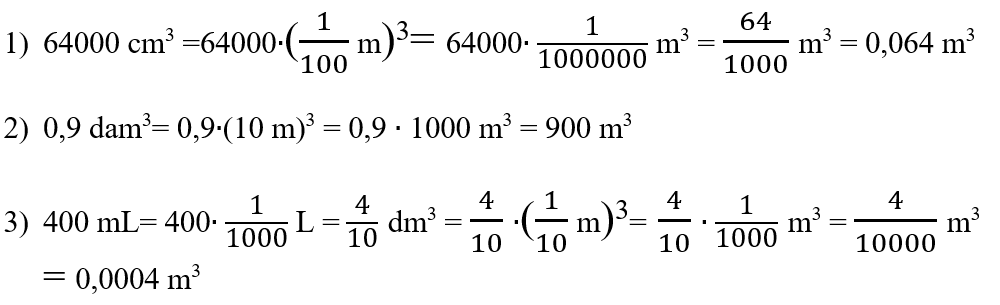
To perform calculations with transformations you need to know the values of multiples and submultiples.

You also need to know very well the operations with fractions:

  • Multiplying two fractions is done by multiplying numerator (number on the fraction line) by numerator and denominator (number below the fraction line) by denominator.
  • The division of two fractions is done by multiplying the fraction from the numerator by the inverse (inverted) of the fraction from the denominator.
👀 Experiment: Measuring the volume of a body with the graduated cylinder

Required materials:
Graduated cylinder, water, string, a body.


Experiment description:

1. The first step is to determine the volume of a division = 1 div = the minimum volume between two consecutive lines. Look carefully at the measurement and find the measurement unit of the cylinder used. How do we proceed?

  • Note two consecutive graduations (one after the other) of the cylinder and subtract them: 50 ml - 40 ml = 10 ml
  • Count how many divisions there are between these notations: 10 divisions = 10 ml
  • With the simple rule of three, we find out the volume of one division:


2. Put water in the cylinder and measure its volume, denoted by V1 = 35 ml.



3. Insert the body into the water in the cylinder. The fluid level has risen. We will note the new volume read V2 = 39 ml.



4. The volume of the body is the difference between V2 (water+body volume) and V1 (water volume), ie:

Vbody = V2 – V1


Remark:

The graduated cylinder must be on a horizontal surface (on the table). The free surface of the liquid is slightly curved (called the meniscus) - higher at the contact of the liquid with the walls of the graduated cylinder. Position the eyes at the free surface of the liquid and read the volume at its base.


Experiment conclusion:

The volume of the body is the difference between V2 (water volume + body) and V1 (water volume), ie:

Vbody = V2 – V1

Vbody = 39 ml – 35 ml = 4 ml.