Skip to main content

II.2.6.1. Overview

📚

The time interval represents the duration of an event.

📚

Characterization of time (duration of an event) as a physical parameter:




Other measurement units for time interval are:

  • Minute = 1 min = 60 s
  • Hour = 1 h = 60 min = 60 ∙ 60 s = 3.600 s
  • Day = 24 h = 24 ∙ 3600 s = 86400 s
  • Week = 7 days = 7 ∙ 86400 s = 604800 s
  • Moon = 30 days = 30 ∙ 86400 s = 2592200 s
  • Year = 365 days = 365 ∙ 86400 s = 31536000 s
🔦 Remark

The Romans called the hours before noon ante meridiem (before noon), and those in the afternoon, post meridiem. Today, they are abbreviated a.m. and p.m. and are used with the meaning of morning and afternoon.

If you use the electronic stopwatch on the phone, which also measures hundredths of seconds, then its accuracy has increased to 0.01s. On the other hand, if you use a ticker, its accuracy is lower and the error can be 1s .

👀 Experiment: Measuring the period of a pendulum with a stopwatch

Required materials:
Ball or nut, thread, stopwatch (you can use the phone)


Experiment description:

  • Take a small and heavy body (a ball, a nut, a key, etc.) and tie it to the end of a wire to get a pendulum. Attach the wire to a horizontal support (for example, a table).

  • Remove the wire from the (vertical) equilibrium position and lift it to one side. Then release it and the pendulum will move to either side of this position, ie it will start to oscillate. The stopwatch starts when the body is released.

  • Measure the time interval (t) in which the body returns a number of times "n" to point A ("n" can have different values: 3, 5, 8, 10 etc. - as much as you want).

  • Repeat the operation at least 3 times, giving it to "n" different values.

  • Calculate the period (T) = the time in which the body makes a complete oscillation, ie the time in which the pendulum climbed to the other side and returned to the initial position (round trip). If in a time "t" are performed "n" full oscillations, then the period (T) is calculated using the relation:




  • Fill in an experimental data table using the below template.


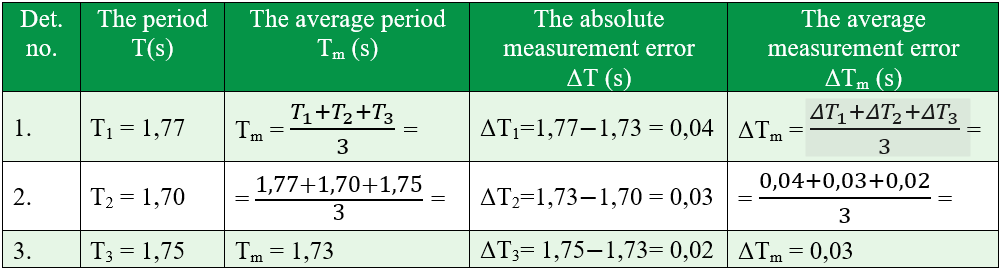
Experiment conclusion:
Write the measurement result: T = Tmean ± ΔTmean = 1,73 ± 0,03 (s)

🔓 Solved problem

1. A movie broadcast on a TV station started at 20:30 and ended at 22:20. If he was interrupted by four commercials, each lasting 8 minutes, how long did the film last, expressed in hours, minutes and seconds?

Solution:

We calculate the broadcast time of both the film and the advertisement, subtracting the end time from the start time of the film: to decrease the minutes, I borrow from the unit of hours by one hour, ie 60 minutes and add them to 20 minutes and say 80 min - 30 min = 50 min.
Then decrease 21 h - 20 h = 1h. 22:20 - 20:30 = 1 h 50 min = t1.

We calculate the time of the advertising blocks (sequences): t2 = 4 ∙ 8 min = 32 min

To find out the length of the movie only, subtract t2 from t1:

tmovie = t1 – t2 = 1 h 50 min – 32 min = 1 h 18 min
tmovie = 60 min + 18 min = 78 min = 78 ∙ 60 s = 4680 s


To find out the duration in hours we transform 18 min into h with the simple rule of 3: