II.2.2. Direct area measurement

The area of a surface shows how large that surface is.

Characterization of the area as physical parameter:

Square meter multiples and submultiples are also used.

🔦 Remark

Here's how to make these transformations from multiples and submultiples of m² to m²:

• Write the numerical value and open a parenthesis, in which the value of the given multiple or submultiple is written, close the parenthesis and raise everything to the respective power, ie to the square.
• Copy the given value again and multiply by the values in parentheses raised to the second power.
• The corresponding mathematical calculations are made and the result is given.

Examples of transformations from multiples and submultiples of m² into m²:

Direct measurement of the area is done using graph paper. On it, thin vertical and horizontal lines are drawn, delimiting squares with a side of 1 mm and an area of 1 mm², and thicker lines, delimiting squares with a side of 1 cm and an area of 1 cm².

👀 Experiment no. 2: Direct measurement of the area of a leaf with graph paper.

Required materials:
Graph paper, leaf, pencil.

Experiment description:

• Draw on the graph paper (you can also use a math sheet that has a side of 0,5 cm and an area of 0,25 cm², but the result will not be too precise) the contour of the leaf (you can choose any shape you want, not necessarily a leaf).
• Count the whole squares with an area of 1 cm² (those outlined with a blue marker), then those with an area of 0.25 cm² (those outlined in yellow), and group the whole ones and approximate them as whole squares with area of 0.25 cm². If you have patience, you can stop approximating the whole squares and count the small squares with the area of 1 mm² and their number multiplied by 1 mm² to turn it into cm², by dividing the result by 100.
• To calculate the area of the leaf (S), apply the formula: S = n ∙ Su, where n = no. squares and Su = area of the chosen unit (either cm² - the largest, or 0.25 cm² - the smallest).
• Draw the outline of the leaf on another graph paper and repeat the above operations so that you have at least three values of the area of the leaf of your choice.

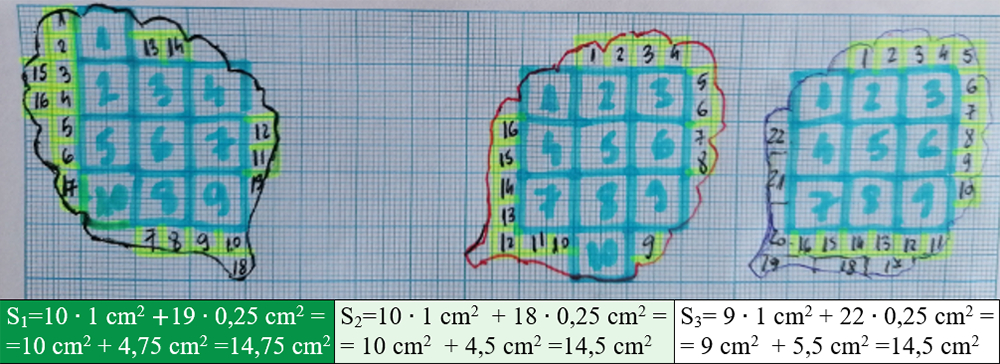
• Fill in the experimental data table and process the data in the table.

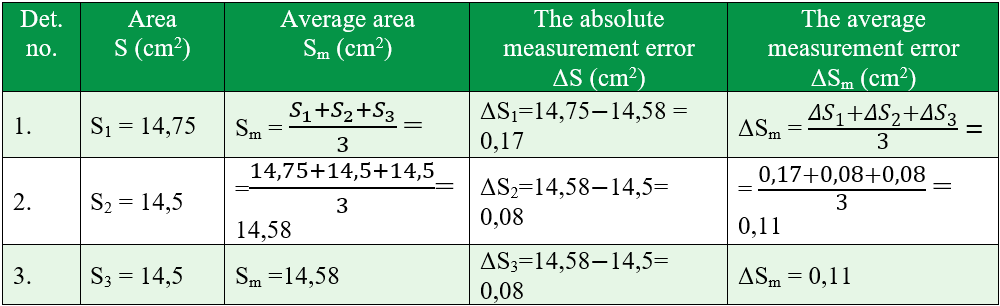
Experiment conclusion:
So the real area of the leaf is: S = S_average ± ΔS_average = 14,58 cm² ± 0,11cm².

The real result of the leaf area: S = S_average ± ΔS_average.