II.2.1.3. Measurement error
Any measurement has limited accuracy and therefore the notion of measurement error appears.
Sources of error can be:
- lack of accuracy of the measurement instrument;
- incorrect reading of the instrument indications;
- the lack of attention or skill of the person making the measurements;
- unfavorable environmental conditions (inadequate lighting, too hot or too cold, discomfort, etc.).
If we perform length measurements with a ruler, the measurement accuracy cannot exceed the smallest gradation of the ruler - respectively 1 mm.
So the measurement error due to the instrument used is equal to the smallest division of the instrument.
At the micrometer the measurement error decreases to 1 micron, ie one millionth of a meter (1 / 1000000).
The existence of measurement errors in the case of experimental determinations is normal and in order to obtain a result as close as possible to the true value of the measured quantity, the measurements are repeated several times and the experimental data are processed as I will show you in the next experiment.
Required materials:
Graduated ruler, pencil.
Experiment description:
- Use the graduated ruler to measure the length of the physics book.
- Measure the length of the physics book several times (at least 3 times), taking care to measure correctly each time.
- Fill in the following table of experimental data: you will pass your determinations and follow the steps according to the following model:
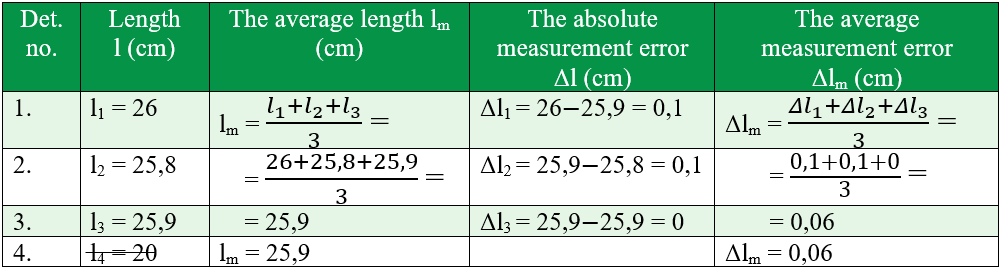
- Processes experimental data.
- l is the length measured at least three times. I measured it four times, but the last value of 20 cm I excluded it, as it is far from the other values, being a rough measurement.
- lm is the average length, ie the arithmetic average of the three measured lengths. If some values appear very different from the others, they are written in the table, but they are cut, they represent gross errors. They are not taken into account in the calculation of the average length. The arithmetic average is equal to the ratio of the sum of all lengths to the number of determinations.
- Δl is the absolute error, which is calculated by the difference between the measured length and the average length (the largest minus the smallest): Δl = l1 – lm sau Δl = lm – l1.
- Δlm is the absolute average error, which is calculated by making the arithmetic average of the absolute errors.
- After completing the table with experimental data, you must write the result of the determination, using the same number of decimals for all numbers. We will write the values with two decimal places, by rounding.
For our example: L = 25,9 cm ± 0,06 cm.
Experiment conclusion:
This result indicates that the actual value is in a range: 25,9 cm – 0,06 cm ≤ l ≤ 25,9 cm + 0,06 cm
So the real length of the physics book is: 25,84 cm ≤ l ≤ 25,96 cm.
Result of the determination = The average value ± The absolute average error
l = laverage ± Δlaverage
1. Florin wants to determine the real value of the length of the kitchen table.
Following the measurements he found the following values: 1,5 m; 1,46 m; 1,6 m ; 1,2 m; 1,56 m. How did he proceed?
Solution:
He calculated lm = The average length, ie the arithmetic average of the four measured lengths. The value of 1.2 m is very different, it is cut and not taken into account in the calculation of the average length, being a rough measurement.
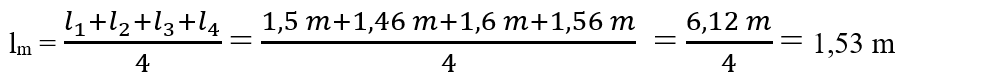
He calculated for each measurement Δl = absolute error, which is calculated by the difference between the measured length and the average length (the largest minus the smallest); Δl = l1 – lm sau Δl = lm – l1.
Δl1 = 1,53 - 1,5 = 0,03 m
Δl2 = 1,53 - 1,46 = 0,07 m
Δl3 = 1,6 - 1,53 = 0,07 m
Δl4 = 1,56 - 1,53 = 0,03 m
He calculated Δlm = the absolute average error, which is calculated by making the arithmetic average of the four absolute errors.
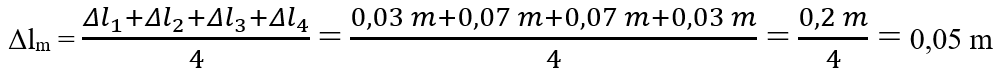
Florin wrote the result of the determination, using the same number of decimals for all numbers (values with two decimals, by rounding).
Result of the determination = The average value ± The absolute average error
l = laverage ± Δlaverage = 1,53 m ± 0,05 m.