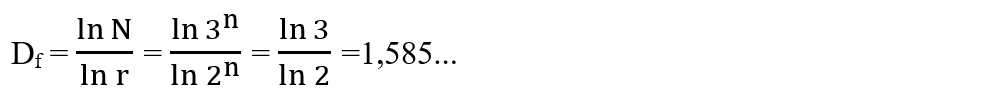IV.5.4. Triunghiul lui Sierpinski
Triunghiul lui Sierpinski (magia puterilor lui 3) are ca inițiator un triunghi echilateral.
- La prima iterație eliminăm triunghiul dat de mijloacele laturilor triunghiului echilateral inițial. Păstrăm triunghiurile din vârfurile triunghiului iniţial (3 copii cu latura la jumătate din latura triunghiului mare).

- La a doua iterație, aplicăm aceeaşi transformare în fiecare dintre cele trei triunghiuri rămase.

- La a treia iterație, aplicăm aceeaşi transformare fiecăruia din cele nouă triunghiuri rămase.

- La a patra iterație, aplicăm aceeaşi transformare fiecăruia din cele douăzeci și șapte triunghiuri rămase.

*Triunghiul lui Sierpinski este mulțimea punctelor rămase după ce repetăm transformarea de mai sus de o infinitate de ori.

- În cazul triunghiului lui Sierpinski, după n iterații dimensiunea Hausdorff este: