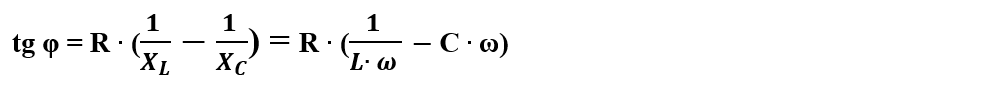II.1.6. Circuit paralel RLC.
Studiul comportării unui circuit paralel RLC se poate face realizând un circuit format dintr-un rezistor, o bobină, un condensator variabil și o sursă de tensiune alternativă, toate legate în paralel.

Tensiunea alternativă la bornele circuitului paralel RLC este:

Tensiunea efectivă U este aceeași la bornele celor trei elemente de circuit legate în paralel.
Cele trei regimuri de funcționare ale unui circuit paralel RLC în curent alternativ sunt:
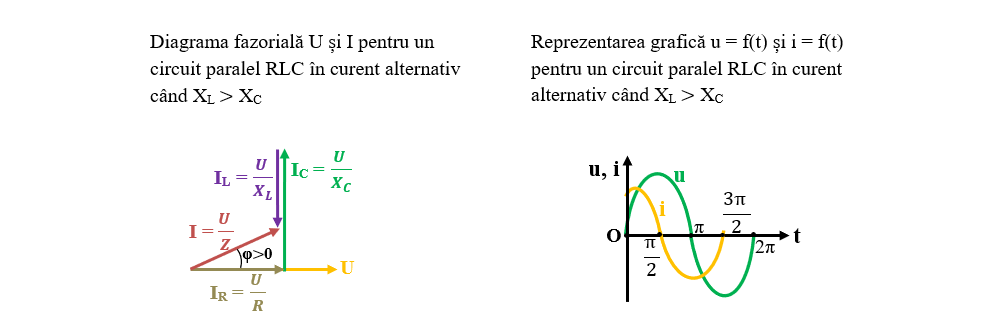
1. Cazul XL > XC
2. Cazul XL < XC

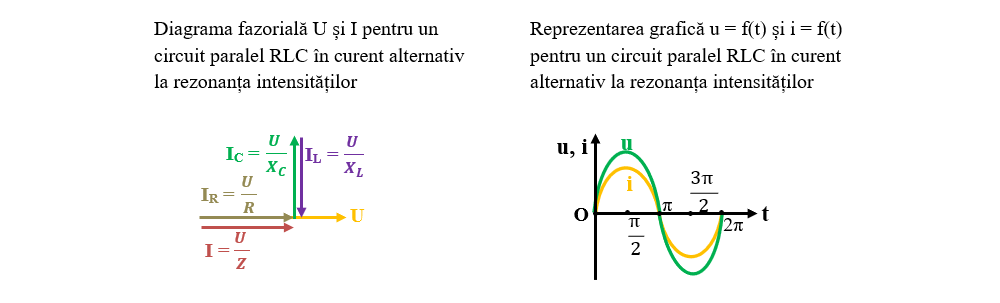
3. Dacă XL = XC, intensitatea curentului este în fază cu tensiunea (φ = 0) și are loc rezonanța intensităților.
Prin cele trei ramuri ale circuitului se stabilesc curenți cu intensitățile:

Aplicând teorema lui Pitagora în triunghiul intensităților obținem:

Mărimea Z, numită impedanța circuitului paralel RLC este definită de relația:

Defazajul φ între tensiunea la bornele circuitului paralel RLC și intensitatea curentului alternativ: