V.4.2. Determinarea centrului de greutate al corpurilor omogene.

Centrul de greutate al unui corp omogen și cu formă geometrică regulată depinde de elementele geometrice ale corpului, nu și de natura materialului din care este confecționat.

Dacă aceste corpuri au un plan, o axă sau un centru de simetrie, atunci centrul de greutate se găsește în planul, pe axa sau în centrul de simetrie respectiv.

Centrul de greutate (C) al plăcilor omogene cu formă geometrică regulată:

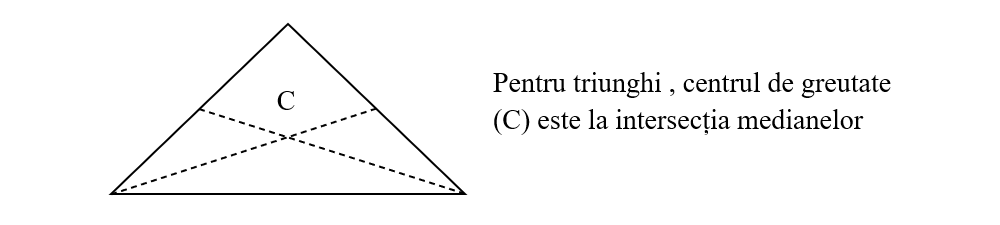
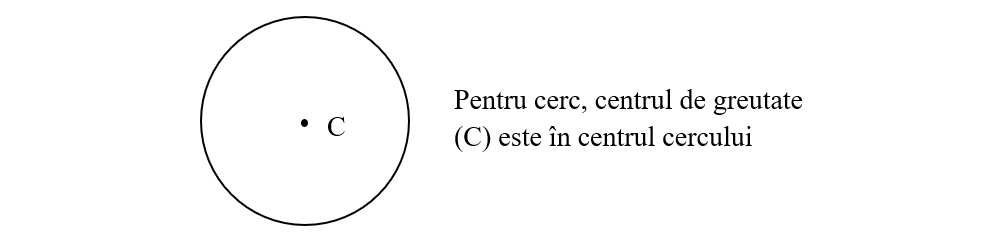
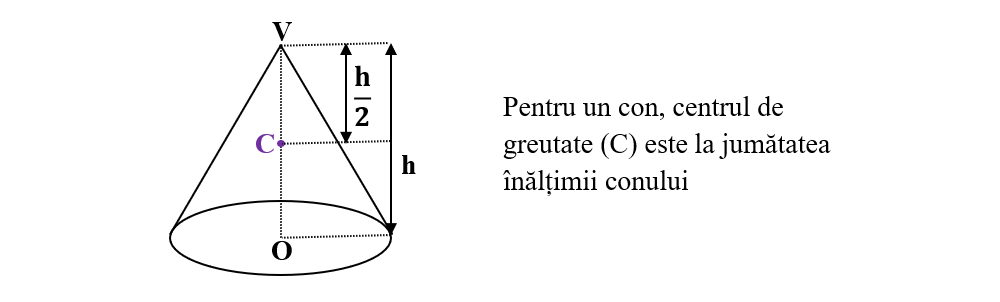
Centrul de greutate al corpurilor omogene cu formă geometrică regulată:

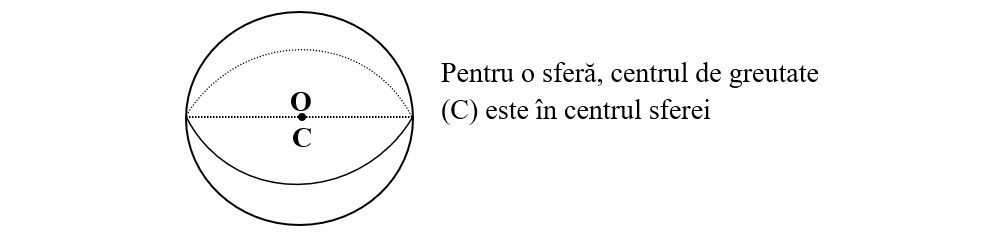
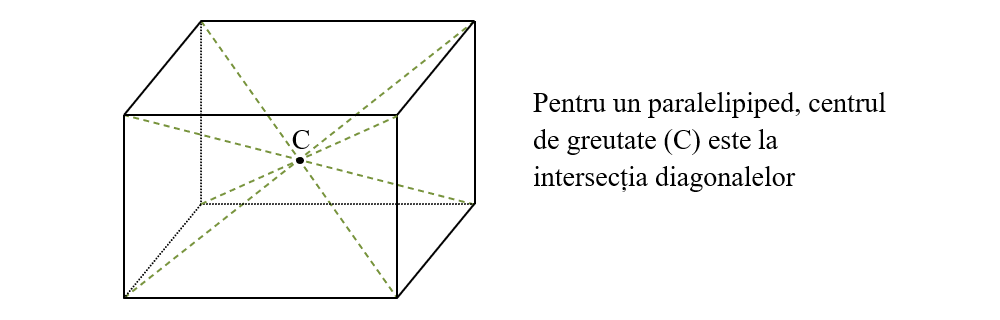
Pentru a determina centrul de greutate al unei figuri ce poate fi descompusă în mai multe figuri cu formă regulată putem folosi legea pârghiei, astfel:

• Descompunem figura cu care lucrăm în două figuri regulate (simetrice);
• Găsim poziția centrului de greutate pentru fiecare dintre figuri;
• Unim cele două centre de greutate. Centrul de greutate al întregii figuri se găsește pe segmentul de dreaptă care unește cele două centre.
• Calculăm poziția centrului de greutate din condiția ca față de punctul respectiv momentele celor două forțe de greutate să fie egale (echilibru de rotație).

Fie o figură formată din două dreptunghiuri așezate ca în figura următoare. Se dau masele celor două corpuri (m₁ și m₂) și lungimile celor două dreptunghiuri (a și b). Determină poziția centrului de greutate al figurii date.

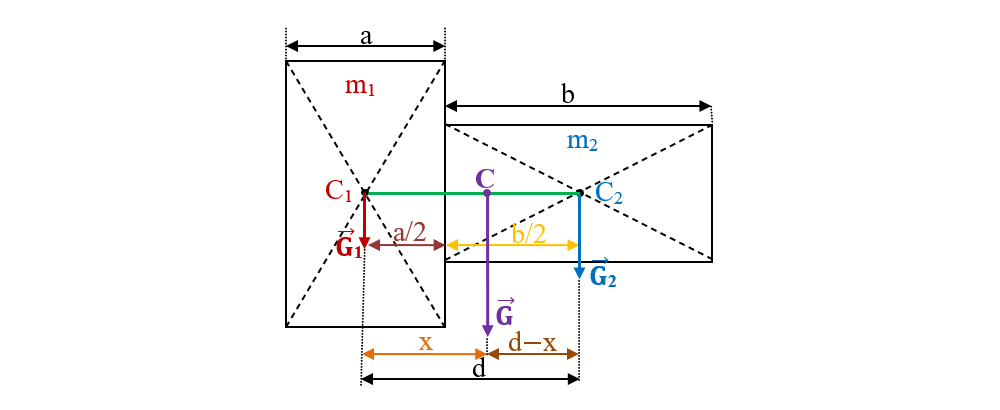
- Notăm cu:

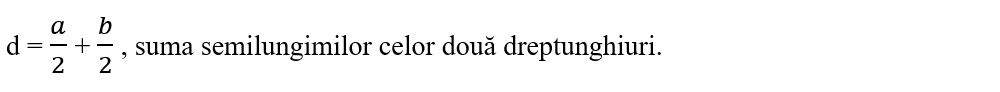
x = C₁C, distanța de la centrul de greutate al dreptunghiului 1 (C₁) până la centrul de greutate al figurii date (C).

d - x = C₂C, distanța de la centrul de greutate al dreptunghiului 2 (C₂) până la centrul de greutate al figurii date (C).