V.2.5. Descompunerea forțelor.
- V.2.5.1. Descompunerea unei forțe în componente concurente.
- V.2.5.2. Descompunerea unei forțe în două componente paralele cu ea.
V.2.5.1. Descompunerea unei forțe în componente concurente.
Descompunerea unei forțe în componente concurente este în ordinea inversă compunerii forțelor cu regula paralelogramului.
Iată câteva exemple:
- La planul înclinat descompunerea forței de greutate se face după două direcții perpendiculare între ele.
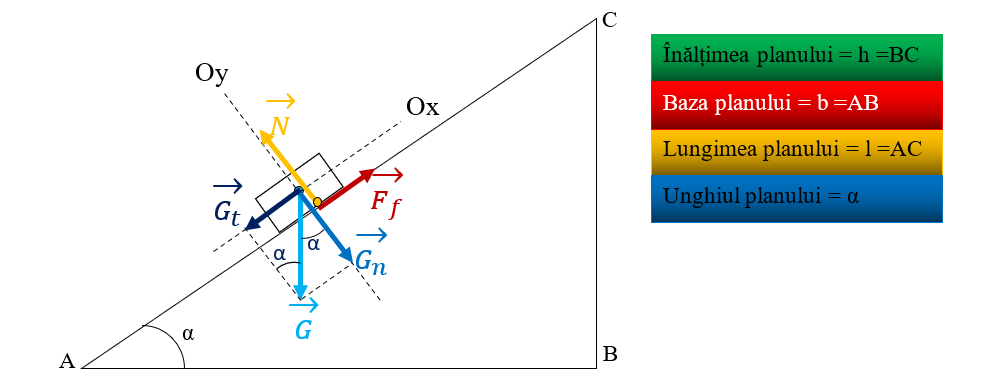
Corpul lăsat liber pe planul înclinat coboară uniform atunci când:
|Ff| = |Gt| și |N| = |Gn|
- Pendulul matematic
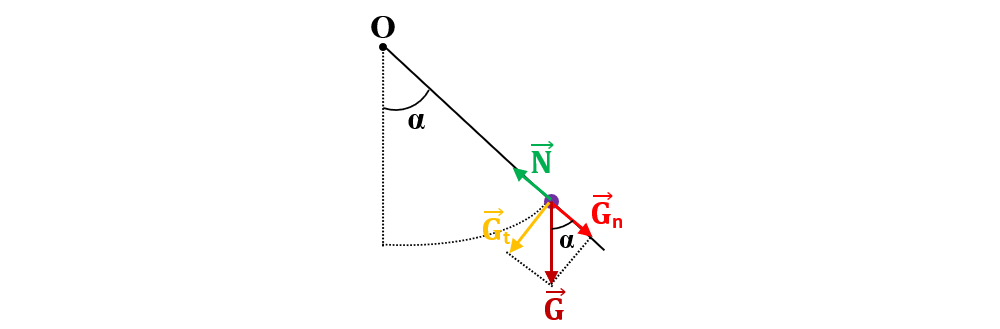
|Gn| = |N| = G ∙ cos α
|Gt| = G ∙ sin α, această componentă pune în mișcare pendulul în jurul poziției de echilibru.
- Consola este un sistem de două bare AB și AC pe care stă sprijinit un corp cu greutatea G.
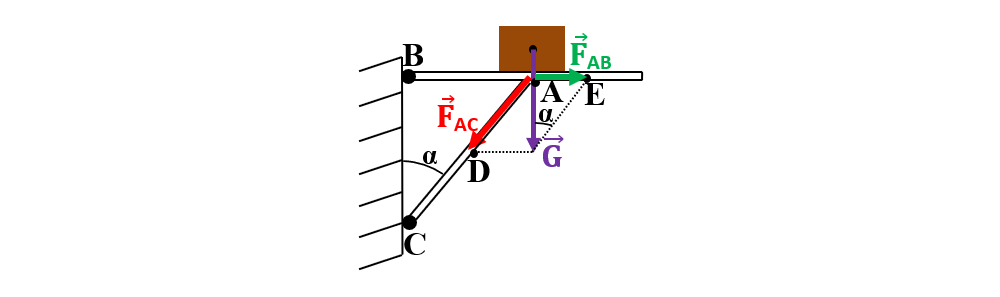
Componentele greutății după direcțiile celor două bare se determină din ΔADE:

V.2.5.2. Descompunerea unei forțe în două componente paralele cu ea.
Descompunerea unei forțe în două componente paralele cu ea:

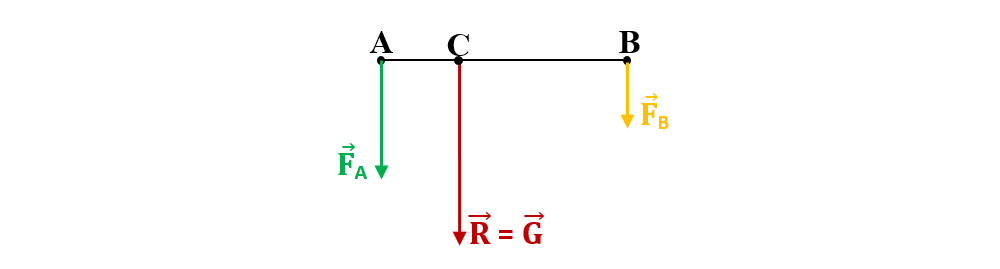
R = G = FA + FB
Din legea pârghiilor avem:

Aplicând proprietățile proporțiilor obținem:


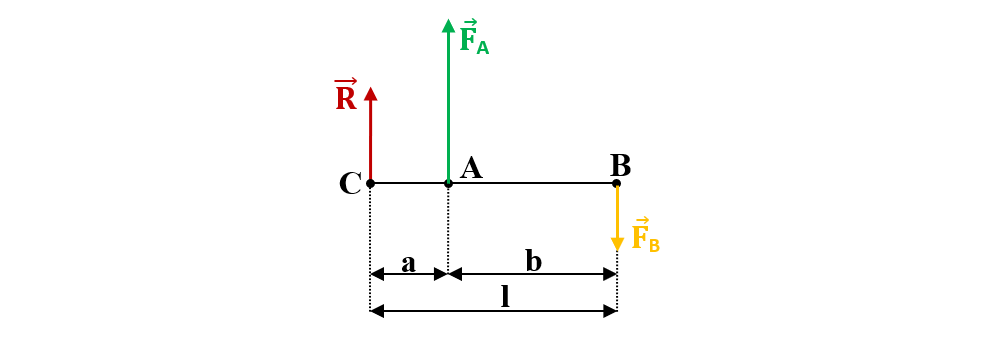
R = FA - FB
