IV.7.2. Teorema variației impulsului.
Considerăm o forță medie, constantă pe un interval de timp Δt, care produce o accelerație medie (o variație de viteză). Putem scrie principiul II al dinamicii:
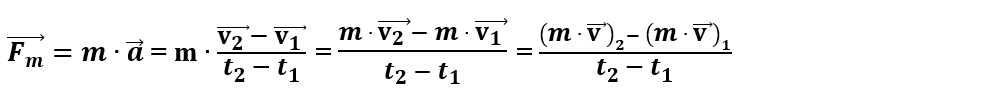
Observăm că apare produsul dintre masă și viteză. Acest produs reprezintă o nouă mărime fizică numită impuls mecanic.

Unitatea de măsură în S.I. pentru impulsul corpului:
[p]SI=[m]SI ∙ [v]SI = 1kg ∙ 1m/s = 1 N ∙ 1 s = N ∙ s


🔦 Observație importantă:
Impulsul este o mărime vectorială care are aceeași direcție și același sens cu vectorul viteză.
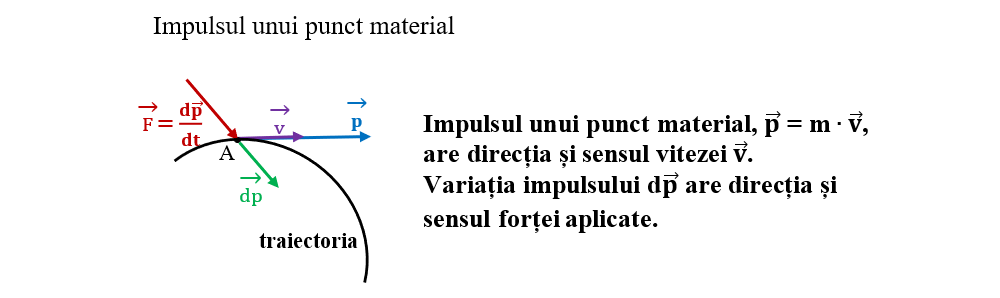
Teorema de variație a impulsului mecanic


🔓 Probleme rezolvate
1. O bilă de 20 g lovește perfect elastic un perete cu o viteză de 10 m/s perpendiculară pe perete, într-un interval de timp de 0,2 s. Cu ce forță acționează peretele asupra bilei? Dar bila asupra peretelui?
Rezolvare:
Notăm datele problemei:
m = 20 g = 0,02 kg
v1 = 10 m/s
Δt = 0,2 s
F = ?
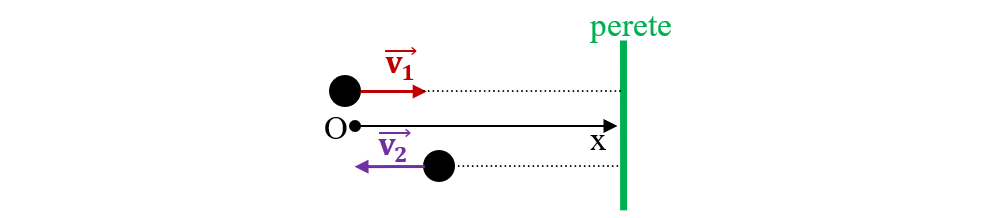

- Forța cu care acționează bila asupra peretelui este egală în modul și de sens opus cu forța cu care acționează peretele asupra bilei:
Fʹ = -F = 2 N
2. O bilă de plastilină de 20 g lovește plastic un perete cu o viteză de 10 m/s perpendiculară pe perete, într-un interval de timp de 0,2 s. După ciocnire bila rămâne lipită de perete. Cu ce forță acționează peretele asupra bilei? Dar bila asupra peretelui?
Rezolvare:
Notăm datele problemei:
m = 20 g = 0,02 kg v1 = 10 m/s Δt = 0,2 s F = ?
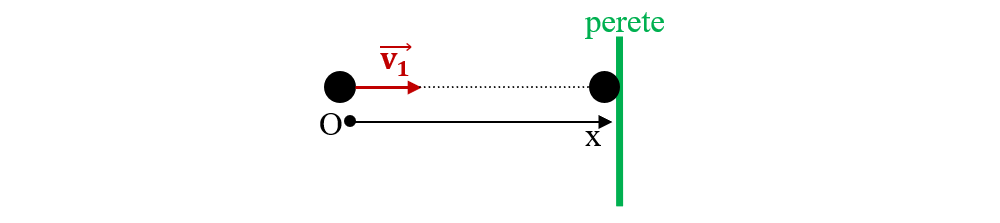

- Forța cu care acționează bila asupra peretelui este egală în modul și de sens opus cu forța cu care acționează peretele asupra bilei:
Fʹ = -F = 1 N