IV.5. Exerciții și probleme rezolvate – Lucrul mecanic, energia mecanică.
🔓 Exerciții și probleme rezolvate – Lucrul mecanic, energia mecanică
1. Adriana dă cu aspiratorul în camera ei. Efectuează ea un lucru mecanic asupra aspiratorului? Explică răspunsul tău.
Rezolvare:
Adriana efectuează un lucru mecanic asupra aspiratorului deoarece îl deplasează.
2. Maia ține în brațe un pluș. Efectuează ea un lucru mecanic asupra plușului. De ce?
Rezolvare:
Maia, chiar dacă acționează cu o anumită forță asupra plușului, ea nu efectuează un lucru mecanic asupra lui deoarece nu îl deplasează.
3. Ce fel de energie mecanică au următoarele corpuri:
a) Un arc întins?
b) O bicicletă care se deplasează cu 30 km/h?
c) O pasăre dintr-un copac față de sol?
d) Un resort comprimat?
Rezolvare:
a) Energie potențială elastică.
b) Energie cinetică.
c) Energie potențială gravitațională.
d) Energie potențială elastică.
4. Un corp de 400 g se deplasează uniform pe o suprafață orizontală cu 10 m/s în 20 min. Știind că forța de frecare reprezintă 15% din greutatea corpului, se cere :
a) Reprezintă toate forțele ce acționează asupra corpului și află valoarea lor.
b) Lucrul mecanic total.
c) Puterea mecanică produsă de corp.
d) Energia cinetică a corpului în timpul deplasării.
Rezolvare:
Scriem datele problemei și le transformăm în SI:
m = 400 g = 0,4 kg
v = constantă = 10 m/s
t = 20 min = 1200 s
Ff = 15% G
a)
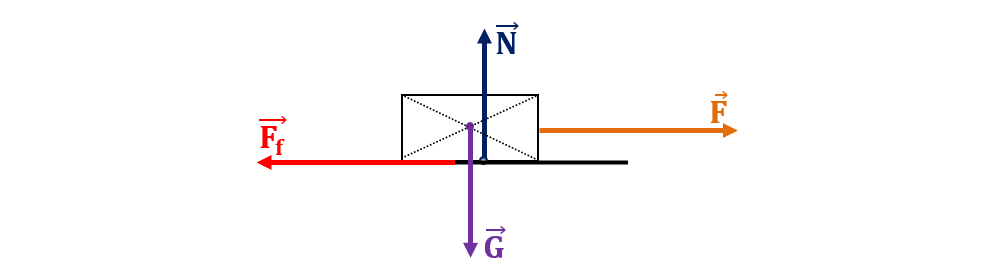
G = m ∙ g = 0,4 kg ∙ 10 N/kg = 4 N
Ff = 15/100 ∙ 4 N = 0,6 N
| F | = | Ff | = 0,6 N, deoarece v = constantă
| N | = | G | = 4 N
b) Ltotal = LF + LFf + LG + LN
LF = F ∙ d = F ∙ v ∙ t = 0,6 N ∙ 10 m/s ∙ 1200 s = 7200 J
LFf = -Ff ∙ d = - F ∙ v ∙ t = -0,6 N ∙ 10 m/s ∙ 1200 s = -7200 J
LG = LN = 0 J
Ltotal = LF + LFf + LG + LN = 7200 J - 7200 J + 0 J + 0 J = 0 J
c)

d)

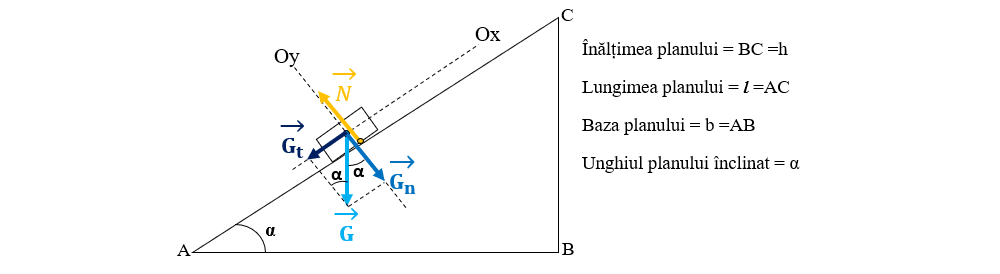
5. Un corp de 1 kg este lăsat să alunece liber pe un plan înclinat, fără frecare, care are unghiul de 30° și lungimea planului de 0,04 dam. Se dă sin 30°=0,5.
a) Desenează forțele ce acționează asupra corpului.
b) Determină lucrul mecanic efectuat de corp în timpul coborârii.
c) Află înălțimea planului înclinat.
d) Determină viteza corpului când ajunge la baza planului înclinat.
Rezolvare:
Notăm datele problemei:
m = 1 kg
Ff = 0
α = 30°
sin 30° = 0,5
l = 0,04 dam = 0,4 m
a)
b)

c)

d)

6. O praștie este confecționată folosind un fir elastic care se întinde cu 4cm, atunci când de el se atârnă o piatră de 80 g. Câtă energie este acumulată în cele șase fire identice ale praștiei întinse, fiecare cu 10 cm? Ce viteză capătă piatra la lansarea cu praștia?
Rezolvare:

Scriem datele problemei și le transformăm în SI:
Δl1 = 4 cm = 0,04 m
m = 80 g = 0,08 kg
Δl2 = 10 cm = 0,1 m
Calculăm constanta elastică a firului, aplicând legea deformării elastice și greutatea pietrei care reprezintă forța deformatoare:
F = k ∙ Δl1 = k ∙ 0,04
G = m ∙ g = 0,08 kg ∙ 10 N/kg = 0,8 N
F = G
0,8 = k ∙ 0,04
k = 0,8/0,04 = 20 N/m
Calculăm energia potențială elastică a unui fir elastic, când praștia este întinsă cu 10 cm:

Deci energia potențială elastică acumulată în cele șase fire ale praștiei este de 0,1 ∙ 6 = 0,6 J.
Energia potențială elastică a praștiei este transferată pietrei la lansarea cu praștia și transformată în energie cinetică:

7. Urcarea uniformă a unui corp cu greutatea de 60 N se face pe o pantă (plan înclinat) cu lungimea de 2m și cu o forță de frecare egală cu 10% din greutatea corpului. Se cere:
a) Lucrul mecanic al forței de frecare.
b) Lucrul mecanic al forței de tracțiune.
c) Lucrul mecanic al forței de frecare când corpul este lăsat să coboare liber spre baza pantei, pe aceeași distanță.
d) Viteza corpului când ajunge la baza pantei.
Se dă: α = 30°; sin 30°= 0,5.
Rezolvare:
Notăm datele problemei:
G = 60 N
l = 2 m
Ff = 10% G
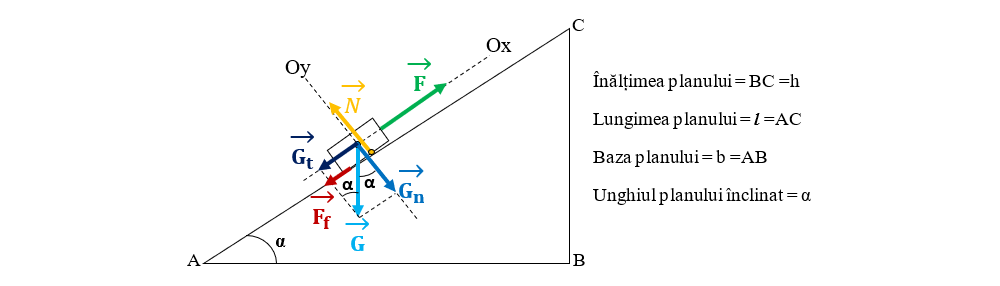
a)
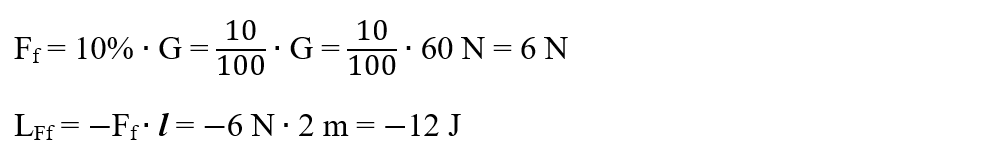
b) Deoarece v = constantă: | F |= | Gt + Ff |

Gt = G ∙ sin 30° = 60 ∙ 0,5 = 30 N
| F | = | Gt + Ff | = 30 + 6 = 36 N
LF = F ∙ l = 36 N ∙ 2 m = 72 J
c) Când corpul coboară liber, forța de frecare este egală cu forța de frecare ca la urcarea pe pantă, deoarece forțele pe direcția Oy rămân aceleași (se schimbă numai forțele pe direcția Ox) :
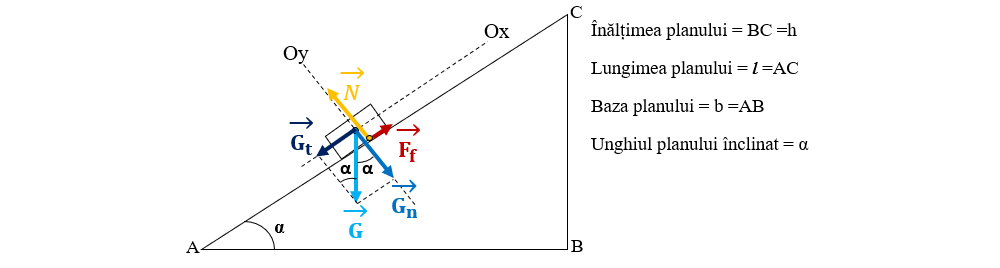
Ff = μ ∙ N = μ ∙ Gt = 6 N
LFf = - Ff ∙ l = - 6 N ∙ 2 m = - 12 J
d) Ca să calculăm viteza corpului cu care ajunge la baza planului înclinat aplicăm Teorema de variație a energiei mecanice:
ΔE = LFf
ΔE = Efinal - Einițial
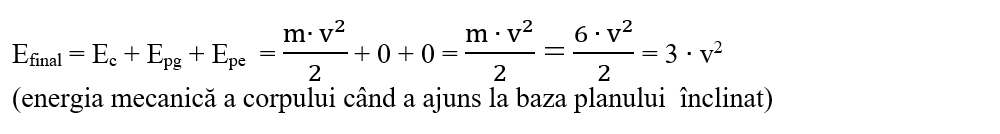
G = m ∙ g = 60 N
m = 6 kg

h = l ∙ sin α = 2 m ∙ 0,5 = 1 m
Einițial = Ec + Epg + Epe = 0 + m ∙ g ∙ h + 0 = m ∙ g ∙ h
Einițial = 6 kg ∙ 10 N/kg ∙ 1 m = 60 J
(energia mecanică a corpului înainte de a coborî pe planul înclinat)
ΔE = Efinal - Einițial = 3 v2 - 60 = - 12
3 v2 = - 12 + 60
3 v2 = 48
v2 = 16 m2/s2
v = 4 m/s
8. Maria aruncă o bilă de 100 g pe verticală în sus de la înălțimea de 2 m față de sol, cu viteza inițială de 2 m/s. Neglijând forța de frecare cu aerul atmosferic, află:
a) Înălțimea maximă la care ajunge bila față de poziția inițială, h0.
b) Viteza cu care bila atinge solul.
c) La ce înălțime urcă bila după ce atinge solul.
d) La ce înălțime maximă (h1') ar ajunge bila când este aruncată în sus cu aceeași viteză inițială, dacă asupra ei ar acționa o forță de frecare de 1N.
Rezolvare:
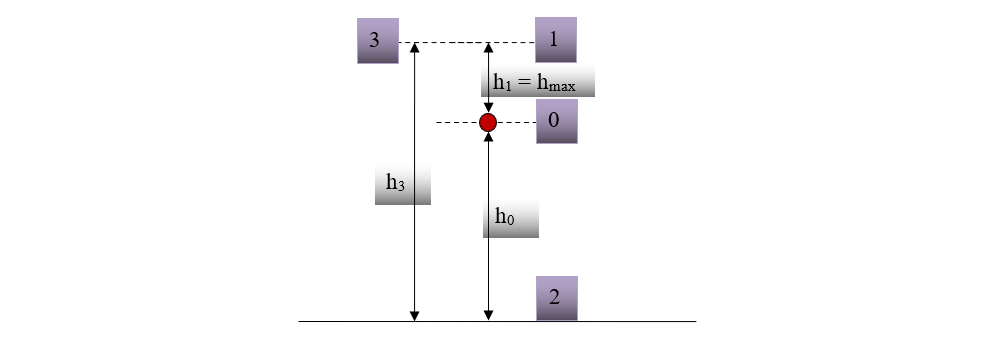
Notăm datele problemei:
m = 100 g = 0,1 kg
h0 = 2 m
v0 = 2 m/s
Ff = 0
a) h1 = hmax = ?
b) v2 = ?
c) h3 = ?
d) h1' = ? când Ff = 1 N
a)
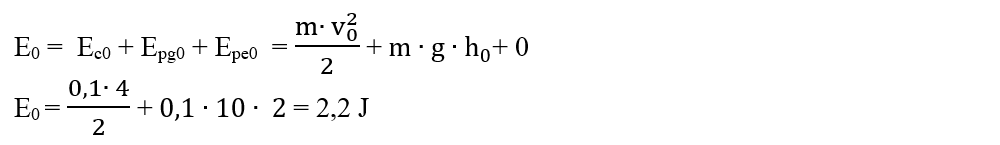
E1 = Ec1 + Epg1 + Epe1 = 0 + m ∙ g ∙ (h1+h0) + 0
E1 = 0,1 ∙ 10 ∙ (h1 + 2) = h1 + 2
Aplicăm Legea conservării energiei mecanice, deoarece Ff = 0:
E0 = E1
2,2 = h1 + 2
h1 = 2,2 m – 2 m = 0,2 m (față de nivelul inițial, h0)
b)

c) E3 = Ec3 + Epg3 + Epe3 = 0 + 0 + m ∙ g ∙ h3 = 0,1 ∙ 10 ∙ h3
E0 = E3
2,2 = h3
h3 = 2,2 m (față de sol)
d) Dacă Ff = 1N, bila nu își mai conservă energia mecanică și aplicăm teorema variației energiei mecanice:
ΔE = LFf
E1' - E0 = - Ff ∙ h1'
m ∙ g ∙ (h1' + h0) – E0 = - 1 ∙ h1'
0,1 ∙ 10 ∙ (h1' + 2) – 2,2 = - 1 ∙ h1'
h1' + 2 – 2,2 = - h1'
2h1' = 0,2
h1' = 0,1 m