IV.4.3. Energia potențială gravitațională.

👀 Experiment: Energia potențială gravitațională

Materiale necesare:
Vas cu făină, două bile de mase diferite.

Descrierea experimentului:

• Ridică o bilă la o anumită înălțime și las-o să cadă liber.
• Ce observi ?

  Bila aflată la o anumită înălțime, lăsată liberă cade.

Corpurile aflate la o anumită înălțime efectuează lucru mecanic atunci când cad, datorită atracției gravitaționale a Pământului. Deci au energie, numită energie potențială gravitațională (de la cuvântul latinesc “potens“ care înseamnă “capabil de ceva“).

• Lasă să cadă de la aceeași înălțime două bile de mase diferite în vasul cu făină.
• Cum sunt urmele lăsate de ele ?

  Bila mai grea lasă o urmă mult mai adâncă decât bila ușoară.

Energia potențială gravitațională a unui corp depinde direct proporțional de masa corpului.

• Lasă să cadă de la înălțimi diferite aceeaşi bilă, în vasul cu făină.
• Cum sunt urmele lăsate de bilă în cele 2 cazuri ?

  Bila care cade de la o înălțime mai mare lasă o urmă mai adâncă decât bila care cade de la o înălțime mai mică.

Energia potențială gravitațională a unui corp depinde de înălțimea la care se află corpul față de sol sau față de un alt nivel de referință.

Energia potențială gravitațională (E_pg) este energia pe care o are un corp aflat la o anumită înălțime față de sol.

Energia potențială gravitațională caracterizează capacitatea unui corp de a efectua lucru mecanic sub acțiunea greutății sale și depinde de poziția corpului în raport cu un nivel de referință.

Energia potențială gravitațională a unui corp este egală cu:

E_pg = G ∙ h = m ∙ g ∙ h

unde:
m este masa corpului
g este accelerația gravitațională
h este înălțimea la care se află centrul de greutate al corpului în raport cu un nivel de referință căruia i se atribuie, prin convenție, o energie potențială nulă.

De exemplu pentru corpurile lăsate să cadă libere în apropierea solului, nivelul de referință pentru care energia potențială gravitațională se consideră nulă este suprafața solului. În general nivelul de referință este ales la nivelul solului sau la nivelul cel mai de jos.

Legea variației energiei potențiale gravitaționale:

“Variația energiei potențiale gravitaționale a unui corp (ΔE_pg) este egală cu lucrul mecanic (L_G) al forței de greutate ce acționează asupra corpului cu semnul minus“ :

ΔE_pg = -L_G

🔦 Observație

Pe măsură ce corpul cade, lucrul mecanic al greutății este pozitiv greutatea având aceeași direcție și același sens cu deplasarea corpului (pe verticală, în jos). Însă energia potențială gravitațională a corpului scade, deoarece scade și înălțimea lui față de sol și deci variația energiei potențiale gravitaționale este negativă.

Energia potențială este o mărime fizică ce caracterizează starea unui corp și se poate defini numai pentru forțe conservative, așa cum sunt greutatea și forța elastică. Ea este o energie stocată, care eliberată produce lucru mecanic.

🔓 Probleme rezolvate

1. Cât este energia potențială gravitațională a unui avion de 30 t la altitudinea de 10 km față de sol?

Rezolvare:

Scriem datele problemei și transformăm în SI:
E_pg = ?
m = 30 t = 30000 kg
h = 10 km = 10000 m

Calculăm energia potențială gravitațională a avionului
E_pg = m ∙ g ∙ h = 30000 kg ∙ 10 N/kg ∙ 10000 m = 3000000000 J

2. Pentru un corp paralelipipedic omogen de masă m, cu dimensiunile h < l < L, determină în ce poziție trebuie așezat pe sol ca să aibă cea mai mică energie potențială, respectiv cea mai mare.

Rezolvare:

Considerăm toată masa corpului concentrată în centrul său de greutate.

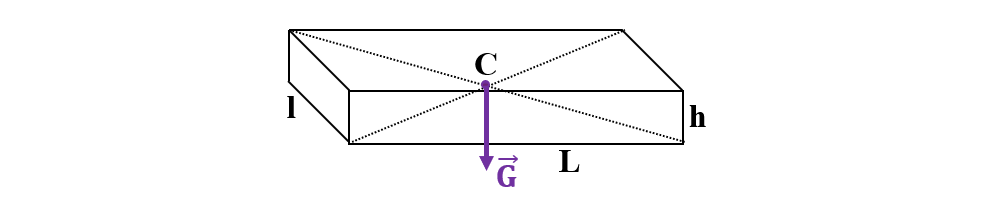
Energia potențială este minimă când distanța de la centrul său de greutate față de sol (nivelul de referință, cu energie potențială 0) este minimă. Acest lucru se întâmplă când paralelipipedul este așezat pe sol cu suprafața cea mai mare, adică cea mărginită de laturile l și L. În acest caz distanța de la centrul său de greutate față de sol este h/2 și avem expresia energiei potențiale minime:
E_pmin. = m ∙ g ∙ h/2

Energia potențială este maximă când distanța de la centrul său de greutate față de sol (nivelul de referință, cu energie potențială 0) este maximă. Acest lucru se întâmplă când paralelipipedul este așezat pe un colț, astfel încât una dintre diagonalele sale (ACʹ) să fie verticală.

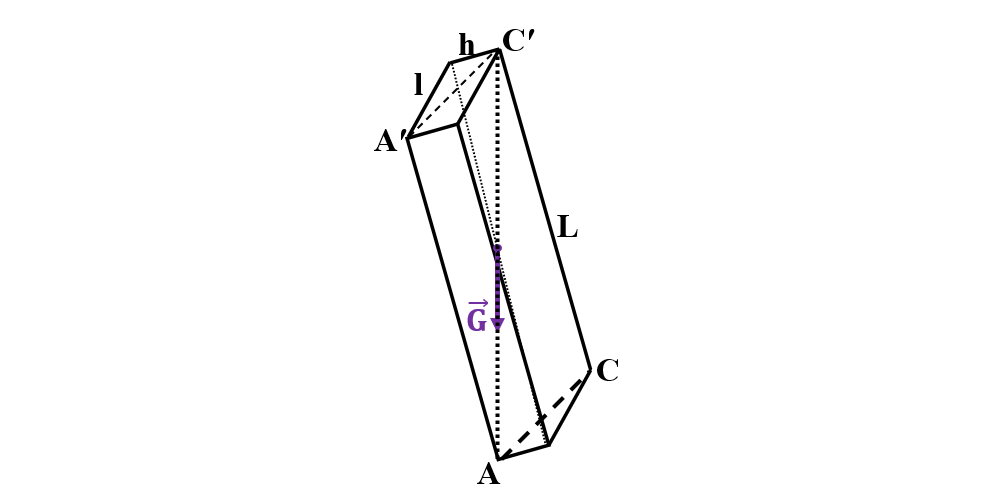
În acest caz distanța de la centrul său de greutate față de sol este jumătate din diagonala paralelipipedului (d/2), adică

Diagonala paralelipipedului este d = ACʹ.

Diagonala bazei este AC² = AʹCʹ² = l² + h²
AAʹ = CCʹ = L
În ΔACCʹ aplicăm teorema lui Pitagora: ACʹ² = CCʹ² + AC²

Expresia energiei potențiale maxime:

3. Un corp este aruncat pe verticală în sus cu o viteză inițială v₀ = 4 m/s. La ce înălțime față de sol energia cinetică a corpului este egală cu energia potențială a sistemului corp-Pământ ?

Rezolvare:

Considerăm nivelul de referință pentru care energia potențială gravitațională este nulă suprafața solului (E_pO = 0).

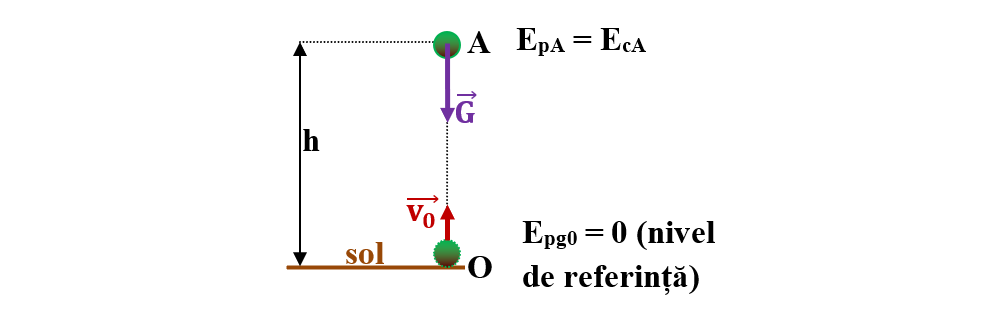
În punctul A, aflat la înălțimea h față de sol avem:

Conform legii variației energiei potențiale gravitaționale, variația energiei potențiale gravitaționale a unui corp (ΔE_pg) este egală cu lucrul mecanic (L_G) al forței de greutate ce acționează asupra corpului cu semnul minus:
ΔE_pg = -L_G

Variația energiei potențiale între nivelele A și O este egală și de semn opus cu lucrul mecanic al greutății pe distanța h (se ia cu semnul minus deoarece la urcare lucrul mecanic este rezistent):

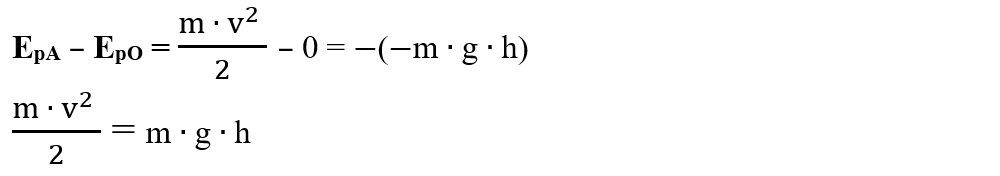
Variația energiei cinetice pe distanța OA este egală cu lucrul mecanic al greutății (acesta se ia negativ deoarece la urcarea corpului greutatea este în sens opus deplasării, adică L_G = -m ∙ g ∙ h):

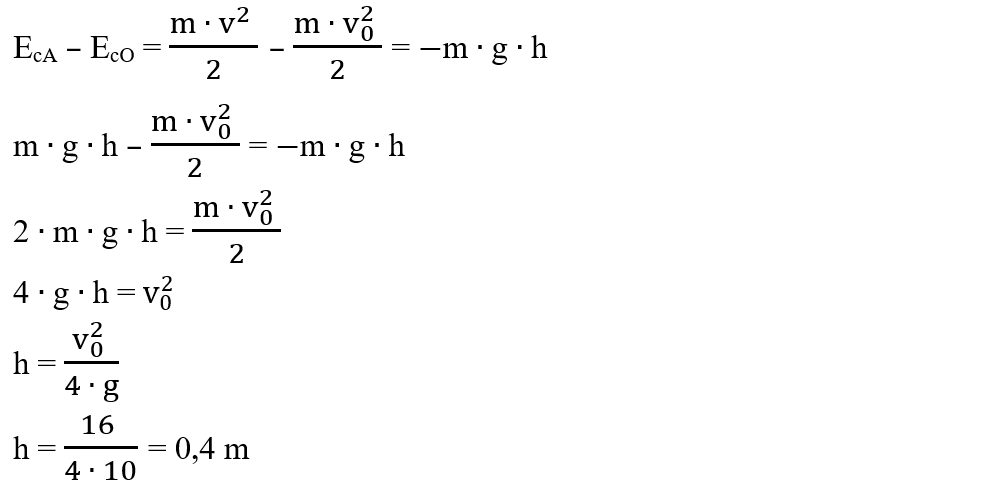
4. O bilă de masă m = 20 g este suspendată de un fir inextensibil cu lungimea l = 0,5 m de un suport. Calculează energia potențială a bilei când bila este ridicată lateral la un unghi de 60° față de poziția verticală (considerată nivel de referință).

Rezolvare:

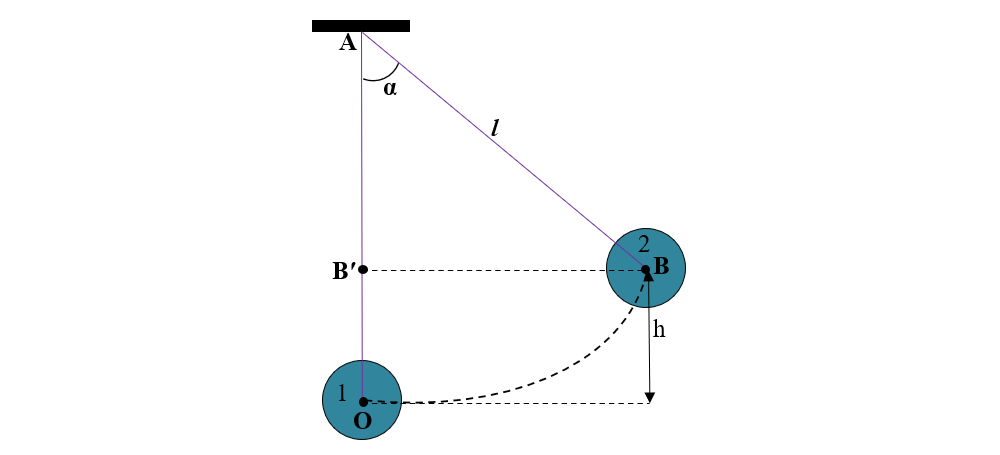
În poziția 2, la înălțimea h față de nivelul de referință, bila are energia potențială:
E_pg = m ∙ g ∙ h

Observăm că ABʹ = l – h și aplicăm cosα în ΔABBʹ și obținem:

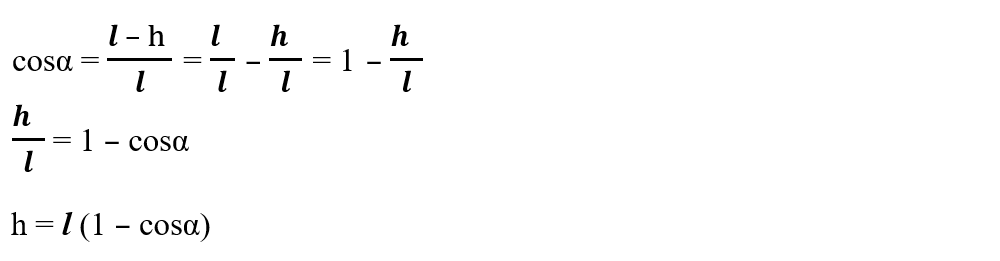
Energia potențială a bilei în funcție de unghiul de deviație:
E_pg = m ∙ g ∙ h = m ∙ g ∙ l (1 – cosα)
E_pg = m ∙ g ∙ l (1 – cosα) = 0,02 kg ∙ 10 N/kg ∙ 0,5 m (1 – 0,5) = 0,05 J