IV.4.2. Energia cinetică.

👀 Experiment: Energia cinetică

Materiale necesare:
2 mașinuțe de mase diferite, plan înclinat din carton, o cutiuță de carton.

Descrierea experimentului:

• Așază la baza planului înclinat cutiuța.
• Pune pe planul înclinat o mașinuță și las-o să alunece pe planul înclinat.
• Ce observi ?

  Mașinuța în mișcare deplasează cutia de la bază planului.

Corpurile în mișcare pot să efectueze lucru mecanic, deci au energie, numită energie cinetică (de la cuvântul grecesc “kineticos“ care înseamnă “mișcare“ ).

• Așază la baza planului înclinat cutia.
• Pune pe planul înclinat o mașinuță mai grea și las-o să alunece pe planul înclinat.
• Repetă experimentul punând pe planul înclinat o mașinuță mai ușoară.
• Apreciază cât se deplasează cutia de la baza planului, în fiecare caz.

  Mașinuța grea deplasează mai mult cutia de la bază planului decât mașinuța ușoară.

Energia cinetică a unui corp în mișcare depinde direct proporțional de masa corpului.

• Înclină mai mult planul înclinat pentru a imprima o viteză mai mare mașinuței.
• Așază la baza planului înclinat cutia .
• Pune pe planul înclinat mașinuța mai grea și las-o să alunece pe planul înclinat.
• Observă cât deplasează cutia de la baza planului în acest caz.

  Mașinuța cu viteză mai mare deplasează mai mult cutia de la bază planului decât mașinuța cu viteza mai mică.

Energia cinetică a unui corp în mișcare depinde de viteza corpului.

Energia cinetică (Ec) este energia pe care o are un corp în mișcare.

Energia cinetică a unui corp este definită prin lucrul mecanic pe care trebuie să-l efectueze un corp din momentul frânării sale până la oprirea sa sau prin lucrul mecanic efectuat pentru a-i imprima o anumită viteză.

Considerăm un punct material în mișcare rectilinie uniform accelerată, sub acțiunea forței F, care se deplasează pe distanța d = x₂ – x₁, de la v₁ la v₂.

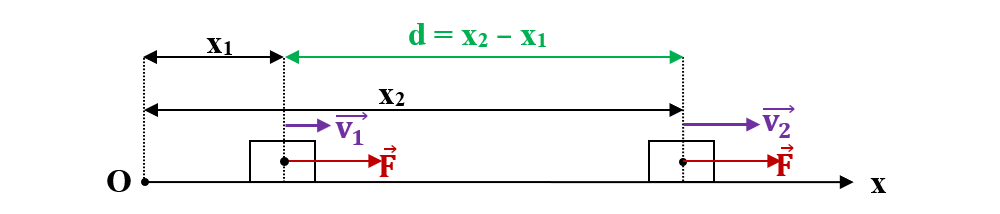
Formula lui Galilei ne dă legătura între cele două viteze :

v₂² – v₁² = 2 ∙ a ∙ d

Din principiul II al dinamicii avem accelerația a = F/m, pe care o înlocuim în formula lui Galilei:

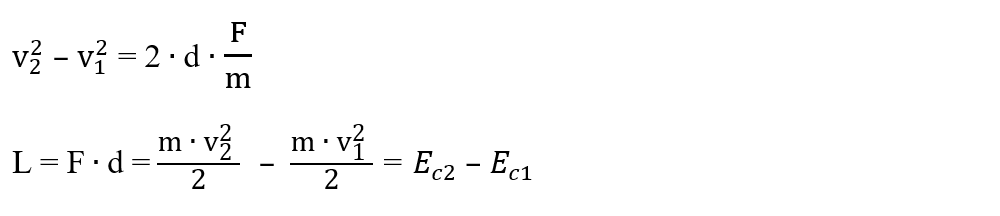
Dacă considerăm v₁ = 0 (corpul este în repaus în starea 1), E_c1 = 0, obținem expresia energiei cinetice a unui corp.

Energia cinetică a unui corp de masă m, în mișcare, cu o anumită viteză v, se calculează cu formula:

Legea variației energiei cinetice:

“Variația energiei cinetice a unui corp (ΔE_c) este egală cu lucrul mecanic (L) al forțelor ce acționează asupra corpului“:ΔE_c = L_total

🔦 Observații importante

• La trecerea unui sistem fizic dintr-o stare în alta se efectuează lucru mecanic. Deci, lucrul mecanic este o mărime de proces, deoarece este asociată cu trecerea sistemului dintr-o stare energetică în alta.

• Energia este o mărime de stare, caracterizând starea sistemului fizic la un anumit moment.

• Schimbarea stării energetice a unui corp se realizează fie prin cedare de lucru mecanic, fie prin primire de lucru mecanic.

Dacă o forță acționând asupra unui corp, efectuează un lucru mecanic motor (L > 0), energia cinetică a corpului crește (v₂ > v₁). De exemplu, când sportivul lovește o minge, aceasta este pusă în mișcare și energia cinetică a mingii crește.

Dacă o forță acționând asupra unui corp, efectuează un lucru mecanic rezistent (L < 0), energia cinetică a corpului scade (v₂ < v₁). De exemplu, când șoferul apasă pedala de frână, mașina frânează sau chiar se oprește și energia cinetică a mașinii scade.

🔓 Probleme rezolvate

1. Un autoturism se deplasează cu viteză constantă pe o șosea rectilinie. La semaforul roșu, șoferul frânează, mașina oprindu-se după 40m. Știind forța de frecare de 2000 N, ce energie cinetică a avut mașina înaintea începerii frânării ?

Rezolvare:

Scriem datele problemei și transformăm în SI:
v = constantă
F_f = 2000 N
d = 40 m
E_ci =? (energia cinetică inițială )

Reprezentăm forțele ce acționează asupra mașinii:

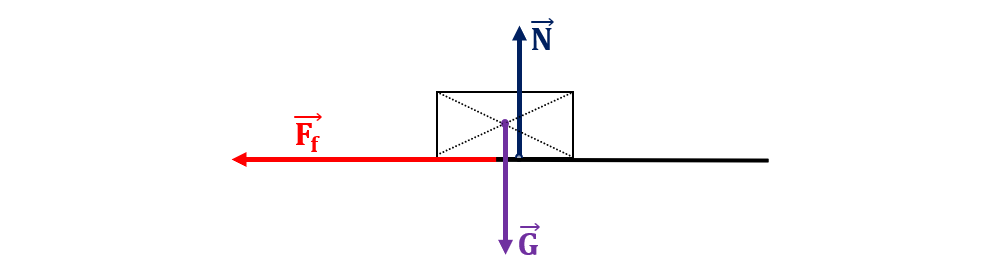
Calculăm lucrul mecanic al tuturor forțelor ce acționează asupra corpului și apoi lucrul mecanic total:
L_Ff = - F_f ∙ d = - 2000 N ∙ 40 m = - 80000 J
L_G = 0 J și L_N = 0 J (deoarece G și N sunt perpendiculare pe direcția mișcării corpului).
L_total = L_Ff + L_G + L_N = - 80000 J + 0 J + 0 J = -80000 J

Calculăm variația energiei cinetice
ΔE_c = E_cf - E_ci = 0 - E_ci = - E_ci , deoarece E_cf = 0 (energia cinetică finală este 0 deoarece mașina s-a oprit și v_f = 0).

Egalăm variația energiei cinetice cu lucrul mecanic (Legea variației energiei cinetice):
ΔE_c = L
-E_ci = L_total
-E_ci = - 80000 J
E_ci = 80000 J

2. O motocicletă de 230 kg pornește din repaus și ajunge la viteza de 20 m/s după ce parcurge 30 m, pe un drum orizontal. Calculează forța de tracțiune a motorului, dacă forța de frecare este de 500 N.

Rezolvare:

Scriem datele problemei:
m = 230 kg
v_i = 0
v_f = v
d = 30 m
F_f = 500 N
F = ?

Reprezentăm forțele ce acționează asupra motocicletei:

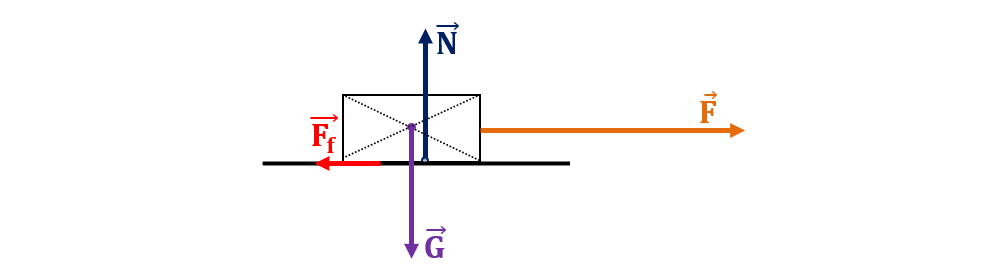
Calculăm lucrul mecanic total prin adunarea lucrurilor mecanice ale forțelor ce acționează asupra corpului:
L_F = F ∙ d = F ∙ 30
L_Ff = - F_f ∙ d = - 500 N ∙ 30 m = - 15000 J
L_G = 0 J și L_N = 0 J (ambele forțe sunt perpendiculare pe direcția mișcării corpului).
L_total = L_F + L_Ff + L_G + L_N = F ∙ 30 – 15000 + 0 + 0 = F ∙ 30 – 15000

Calculăm variația energiei cinetice
ΔE_c = E_cf - E_ci = E_cf - 0 = E_cf, deoarece E_ci = 0 (mașina a pornit și în repaus avea v_i = 0).

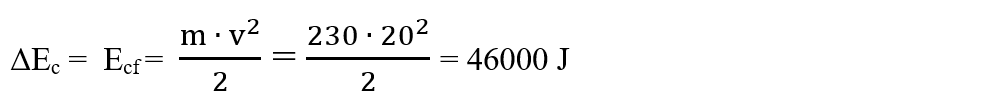
Egalăm variația energiei cinetice cu lucrul mecanic (Legea variației energiei cinetice):
ΔE_c = L_total
46000 = F ∙ 30 – 15000
F ∙ 30 = 46000 + 15000
F = 2033,33 N

Distanţa de frânare

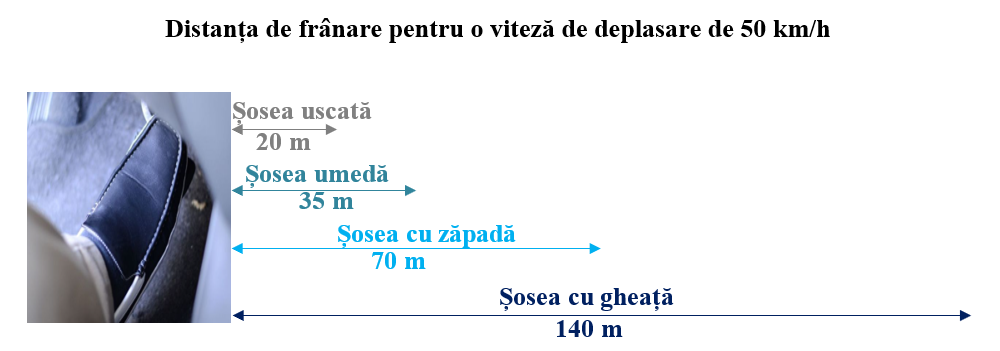
Distanța de frânare a mașinilor este distanța necesară opririi unei mașini, cu ajutorul frânelor. Ea depinde de mai mulți factori :

• Cu cât viteza este mai mare, cu atât și distanța de frânare este mai mare. Iată de ce există limitări de viteză.

• Când aderența la sol este redusă (polei, ploaie, pneuri uzate), distanța de frânare crește.

• Cu cât vehiculul are masa mai mare (un tir încărcat poate avea 40 de tone), cu atât distanța de frânare este mai mare. De exemplu un camion de 40 t are nevoie de 86 m pentru a se opri complet de la 90 km/h.