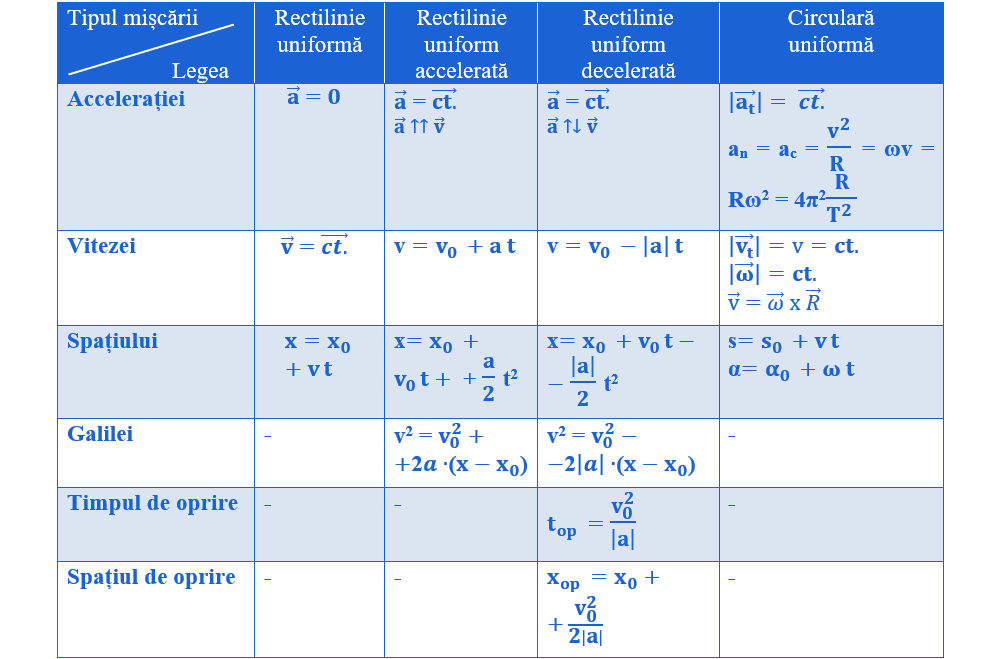
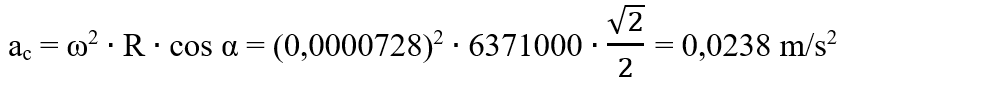III.1.3. Elemente de cinematica punctului material.

• III.1.3.1. Vectorul de poziție.
• III.1.3.2. Viteza medie și momentană.
• III.1.3.3. Accelerația medie și accelerația momentană.
• III.1.3.4. Tipuri de mișcări după traiectorie și viteză.
• III.1.3.5. Mișcarea rectilinie uniformă.
• III.1.3.6. Mișcarea rectilinie uniform variată.
• III.1.3.7. Mișcarea circulară uniformă.

III.1.3.1. Vectorul de poziție.

🔓 Problemă rezolvată

1. Un călător pleacă din origine și parcurge 500 m spre est, apoi merge spre sud 200 m, apoi spre vest 800 m și în final se deplasează spre nord 300 m, ajungând în punctul M față de originea (O). Se cere :
a) Determină vectorul rezultant al celor 4 vectori deplasare.
b) Determină coordonatele vectorului de poziție rezultant față de originea (O) și modulul acestui vector.
c) Cum este modulul vectorului de poziție rezultant față de distanța parcursă de călător ?

Rezolvare:

a) Trasăm un sistem de coordonate alegând axa Ox pe direcția E-V și axa Oy pe direcția N-S.

Reprezentăm grafic cei 4 vectori deplasare și îi compunem cu regula poligonului.

b)

c) Calculăm distanța parcursă de călător:

d = 500 m + 200 m + 800 m + 300 m = 1800 m

Observăm că d > r.

III.1.3.2. Viteza medie și momentană.

Viteza medie (v_m) este mărimea fizică egală cu raportul dintre deplasarea mobilului (d) și durata mișcării (Δt).

1) Formulă de calcul:

2) Unitate de măsură în S.I.:

Vitezometrul aflat la bordul tuturor mașinilor este un instrument de măsură pentru viteza momentană.

Viteza momentană este viteza mobilului la un anumit moment indicată de vitezometru.

De exemplu, o mașină merge cu o viteză medie de 70 km/h pe o porțiune de drum. Asta nu înseamnă că tot drumul mașina a avut această viteză. Vitezometrul poate a indicat chiar și 140 km/h sau 20 km/h.

Viteza medie nu este media aritmetică a vitezelor momentane ale mobilului.

Vom studia viteza medie și momentană a unui mobil pentru două cazuri: mișcarea rectilinie și mișcarea curbilinie.

I. Mișcarea rectilinie (pe o singură axă de coordonată)

Viteza medie a punctului material este dată de relația :

Ecuația vectorială a vitezei medii este:

Pentru a obține relația vitezei momentane plecând de la viteza medie, trebuie să considerăm durata mișcării foarte mică, tinzând către zero.

Dacă Δt→0, atunci și deplasarea Δx→0. Pentru a nu confunda relația vitezei medii cu cea a vitezei instantanee (la un moment dat), vom nota pe Δx→0 cu dx și pe Δt→0 cu dt.

Viteza momentană a punctului material este dată de relația:

🔦 Observație

Viteza are același semn ca și deplasarea, deoarece Δt este totdeauna pozitiv. Viteza este pozitivă dacă mobilul se mișcă în sensul pozitiv al axei (Δx > 0, vm > 0) și este negativă dacă mobilul se mișcă în sensul negativ al axei (Δx < 0, vm < 0).

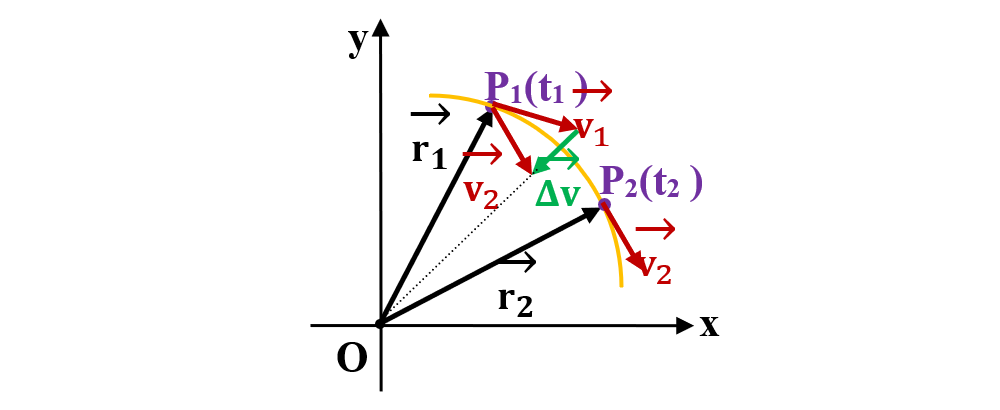
II. Mișcarea curbilinie

Dacă împărțim această ecuație prin Δt, obținem:

În cazul mișcării curbilinii plane, viteza medie a punctului material este:

În cazul mișcării curbilinii plane, viteza momentană a punctului material este:

III.1.3.3. Accelerația medie și accelerația momentană.

Mișcarea rectilinie uniformă este posibilă în viața de zi cu zi, numai pe porțiuni mici de autostradă.

În cazul mișcărilor reale viteza mobilelor crește sau scade în timp, datorită semafoarelor, curbelor, trecerilor de pietoni, limitărilor de viteză.

Toate mașinile au o pedală de accelerație și una de frână.

Pentru a caracteriza variația vectorului viteză, atât în mod, cât și a orientării lui, s-a introdus noțiunea de accelerație.

Vectorul accelerație este îndreptat spre centrul traiectoriei, normal pe aceasta, fiind numită accelerație normală (radială).

Vectorul accelerație instantanee (a_n) se obține prin trecerea la limită a relației accelerației medii (Δt→0), fiind numit accelerație normală (radială), deoarece este orientat normal pe traiectorie :

III.1.3.4. Tipuri de mișcări după traiectorie și viteză.

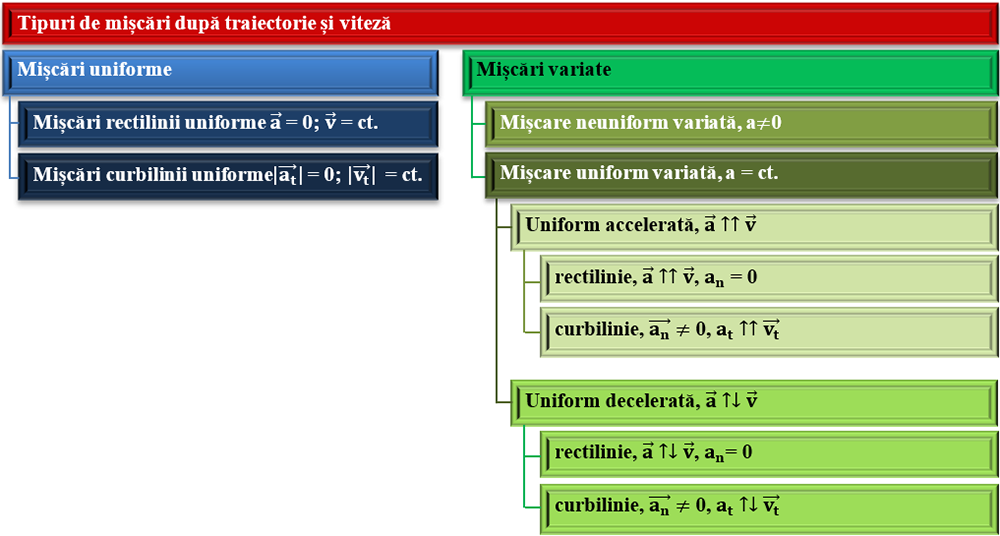
III.1.3.5. Mișcarea rectilinie uniformă.

Mișcarea rectilinie uniformă (MRU) este mișcarea în care traiectoria este o linie dreaptă și viteza constantă în modul, direcție și sens.

În mișcarea rectilinie uniformă :
- Mobilul parcurge distanțe egale în intervale de timp egale.
- Viteza momentană este egală cu viteza medie.
- Viteza își păstrează valoarea numerică, direcția și sensul mișcării.

Pentru a determina legea mișcării rectilinii uniforme, plecăm de la formula vitezei, notând cu x₀ = poziția inițială, cu x = poziția finală, cu t₀ = momentul inițial și cu t = momentul final.

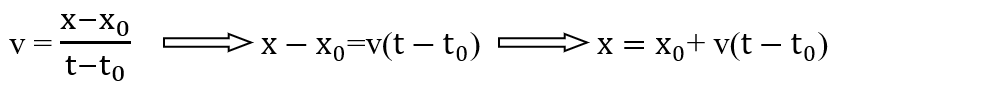
Legea mișcării rectilinii uniforme:

x = x₀ + v(t - t₀) când mobilul se depărtează de reper

x = x₀ - v(t - t₀) când mobilul se apropie de reper.

Legea vitezei în MRU pe axa x este:

Legea accelerației în MRU este:

🔦 Observație importantă

Graficul mișcării rectilinii uniforme este o linie dreaptă, deoarece x = f(t) este o funcție de gradul I în timp.

Dacă notăm cu α unghiul făcut de grafic cu abscisa (axa timpului), putem deduce viteza corpului din panta graficului. Avem două cazuri:

a) Când mobilul se îndepărtează de origine avem panta:

b) Când mobilul se apropie de origine avem panta:

🔓 Probleme rezolvate

1. O scară rulantă ridică un călător, aflat în repaus pe scară, în timpul t₁ = 30 s. Când scara nu merge, călătorul urcă în timpul de t₂ = 20 s. În cât timp (t) urcă călătorul pe scara mobilă (aflată în funcțiune)?

Rezolvare:

Notăm cu v_s – viteza scării, v_c – viteza călătorului față de scara imobilă (fixă) și cu v – viteza călătorului față de sol.

Viteza călătorului față de sol este v = v_c + v_s

Distanța parcursă de călător în cele trei cazuri este aceeași și egală cu lungimea scării:

d = v_s ∙ t₁ = v_c ∙ t₂ = v ∙ t

Calculăm timpul (t) în care călătorul urcă pe scara mobilă:

2. Avem următoarele două grafice. Determină ce fel de mișcare au cele două mobile și legile lor de mișcare.

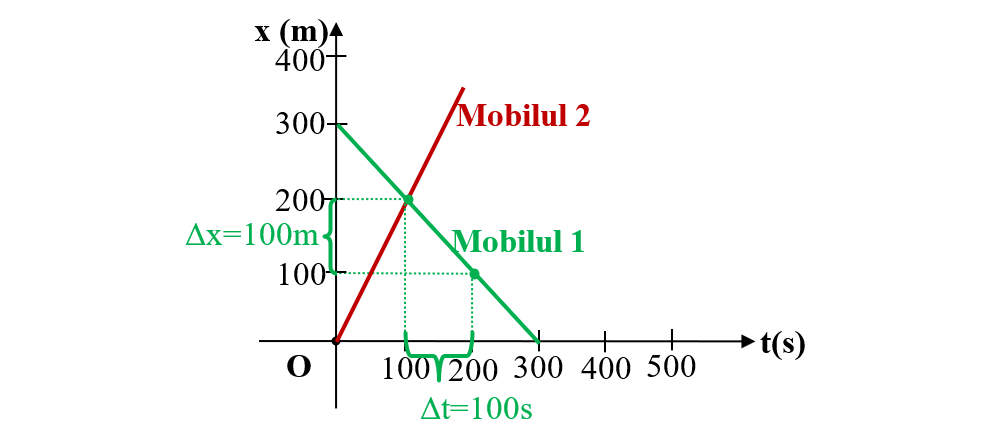
Rezolvare:

Ambele mobile au o mișcare rectilinie uniformă, deoarece graficul x = f(t) este o funcție liniară de timp, fiind o linie dreaptă. Legea MRU este un polinom de gradul I în timp.

Scriem legea mișcării rectilinii uniforme:
x = x₀ + v ∙ t când mobilul se depărtează de reper
x = x₀ - v ∙ t când mobilul se apropie de reper

Pentru mobilul 1 (care se apropie de reper), intersecția graficului cu axa poziției (Ox) este în punctul 300 m, deci x₀₁ = 300 m. Pentru a calcula viteza luăm două puncte pe grafic și ducem de la fiecare punct de pe grafic perpendiculare pe cele două axe pentru a afla Δx, respectiv Δt.
Δx = 100 m
Δt = 100 s

Calculăm viteza cu formula:

Înlocuim datele obținute din grafic în legea mișcării:
x = x₀ - v ∙ t = 300 - 1 ∙ t
x = 300 - t

Pentru mobilul 2 (care se depărtează de reper), intersecția graficului cu axa poziției (Ox) este în punctul 0, deci x₀₁ = 0.

Pentru a calcula viteza luăm două puncte pe grafic și ducem din aceste puncte perpendiculare pe cele două axe pentru a afla Δx, respectiv Δt.
Δx = 100 m
Δt = 50 s

Calculăm viteza cu formula :

Înlocuim datele obținute din grafic în legea mișcării:
x = x₀ + v ∙ t = 0 + 2 ∙ t
x = 2 ∙ t

3. Două trenuri merg unul spre celălalt cu viteza de v₁ = 64,8 km/h, respectiv v₂ = 79,2 km/h. Un pasager din primul tren cronometrează un timp τ = 5 s în care vede al doilea tren trecând prin dreptul său. Care este lungimea trenului al doilea?

Rezolvare:

Scriem datele problemei și le transformăm în SI:
v₁ = 64,8 km/h = 18 m/s (împărțim valoarea vitezei în km/h la 3,6)
v₂ = 79,2 km/h = 22 m/s

Față de călătorul din primul tren, trenul al II-lea are o viteză relativă de v₁ + v₂.

Dacă pasagerul din primul tren cronometrează un timp τ în care vede al doilea tren trecând prin dreptul său, înseamnă că lungimea trenului al doilea este:

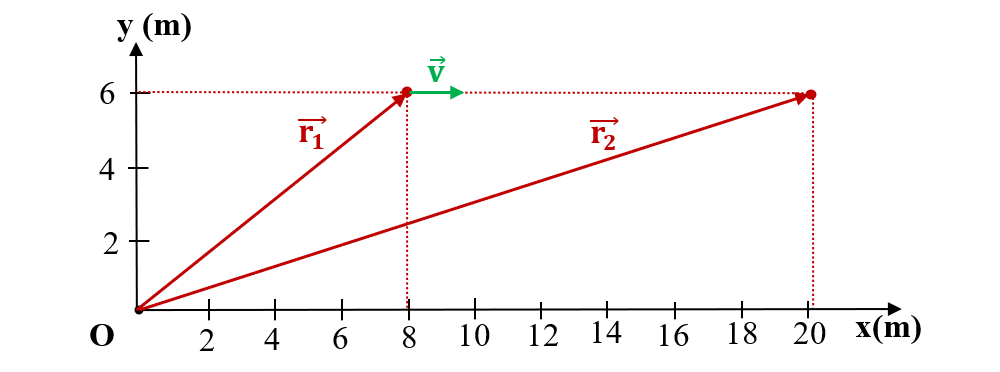
4. Un punct material se află în poziția inițială în punctul P₁ de coordonate: 8 m și 6 m. El se mișcă rectiliniu uniform cu o viteză de 4 m/s, paralel cu axa Ox. După un interval de timp de 3 s ajunge în punctul P₂. Reprezintă vectorii de poziție ai punctului material în cele două puncte și determină modulele lor.

Rezolvare:

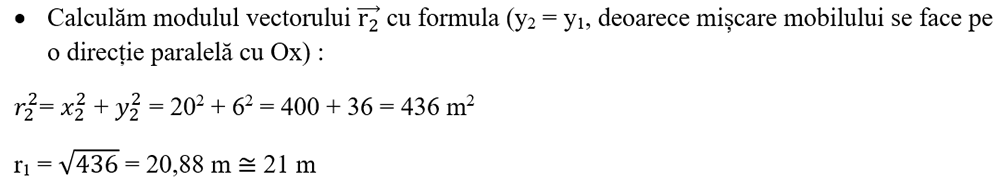
- Reprezentăm grafic cei doi vectori de poziție:

5. Două mobile care se deplasează pe aceeași direcție au următoarele ecuații de mișcare:
x₁ = 3t, respectiv x₂ = 10 – 2t. Determină timpul lor de întâlnire și locul de întâlnire.

Rezolvare:

Scriem condiția de întâlnire pentru cele două mobile :
x₁ = x₂
3t = 10 – 2t
5t = 10
t = 2 s

Pentru a calcula locul de întâlnire, înlocuim timpul t într-una dintre ecuațiile de mișcare:

x₁ = x₂ = 3 ∙ 2 = 6 m

III.1.3.6. Mișcarea rectilinie uniform variată.

Mișcarea rectilinie uniform variată este mișcarea unui mobil pe o traiectorie rectilinie și cu vectorul accelerație instantanee constant în modul, direcție și sens.

Mișcarea rectilinie uniform variată este de două feluri: mișcarea rectilinie uniform accelerată și mișcarea rectilinie uniform decelerată.

Un mobil are o mișcare rectilinie uniform accelerată atunci când modulul vitezei lui crește în timp.

Iată cum arată pozițiile unui mobil la intervale de timp egale în mișcarea rectilinie uniform accelerată:

În mișcarea rectilinie uniform accelerată :
- Mobilul parcurge distanțe din ce în ce mai mari, în intervale de timp egale.
- Accelerația momentană este egală cu accelerația medie, fiind constante.
- Accelerația și viteza au aceeași direcție și sens, ca și cel al mișcării.

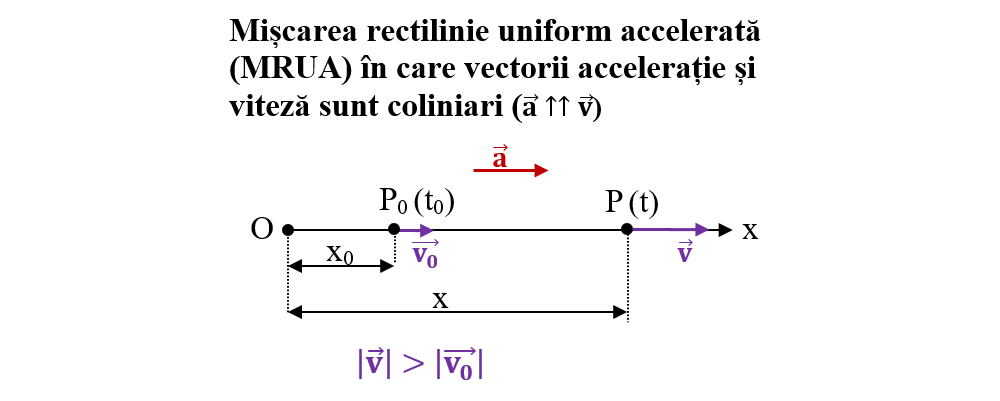
Exemplu de MRUA

Cel mai cunoscut exemplu de mișcare rectilinie uniform accelerată este căderea liberă a corpurilor pe Pământ.

Toate corpurile cad spre Pământ cu o accelerație constantă, numită accelerație gravitațională, g = 9,81 m/s². Când corpul cade liber, viteza inițială a acestuia este v₀ = 0 m/s.

Legea accelerației în MRUA este:

Legea vitezei în MRUA este:

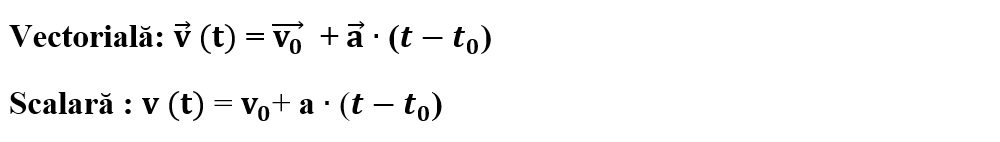
🔦 Observație importantă:

Deoarece în MRUA, în intervalul de timp [t₀, t], viteza mobilului crește liniar cu timpul, se poate calcula viteza medie (v_m) ca medie aritmetică a valorii acesteia la momentele 0 și t, adică:

Legea spațiului în MRUA:

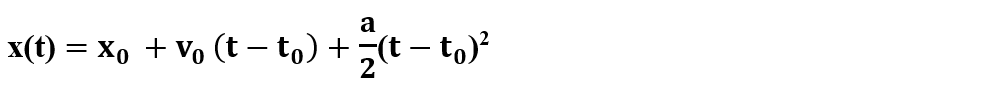
Când avem cazul particular t₀ = 0, legea spațiului devine:

Când avem cazul particular t₀ = 0, v₀ = 0 și x₀ = 0, legea spațiului devine:

🔦 Observație

Legea spațiului în MRUA se obține egalând definiția generală a vitezei medii cu expresia vitezei medii în MRUA:

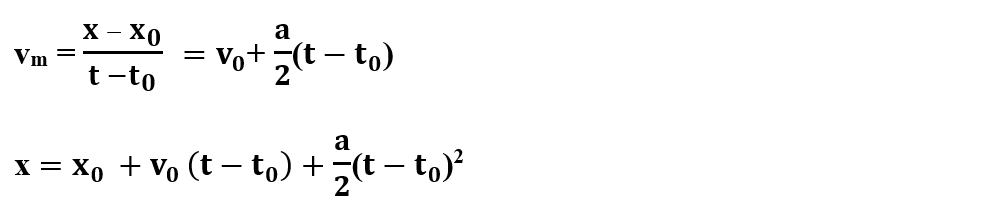
Formula lui Galilei ne permite să calculăm viteza mobilului pentru orice poziție a sa:

v² = v₀² + 2a (x - x₀)

Cazuri particulare:

a) Dacă mobilul pleacă chiar din reper (din O - originea coordonatelor), x₀ = 0, la t = 0, atunci avem relația:

v² = v₀² + 2ax

b) Dacă și v₀ = 0, adică mobilul pleacă din repaus, la t = 0, avem :

v² = 2ax

🔦 Observație

Formula lui Galilei se obține astfel:

- scoatem timpul din ecuația vitezei:

- introducem timpul în legea spațiului și scoatem viteza din ecuația finală :

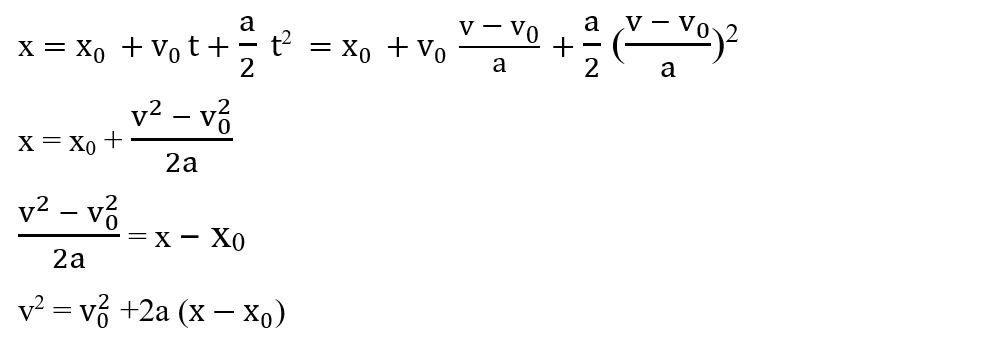
🔓 Probleme rezolvate

1. Privește cu atenție datele despre mișcarea fetei. Cum determinăm tipul mișcării ei ?

Observăm că în intervale de timp egale (de 4 s), fata parcurge distanțe din ce în ce mai mari. Dacă efectuăm calculul vitezelor pe fiecare porțiune, acestea cresc. Vitezele cresc cu valori egale (Δv = 1 m/s) în intervale de timp egale (Δt = 4 s). Cum accelerația este raportul dintre variația vitezei pe intervalul de timp, rezultă că mișcarea este rectilinie uniform accelerată.

2. Pentru a intra într-o depășire, o mașină care se deplasează cu o viteză de 54 km/h, accelerează cu 4 m/s². La ce viteză ajunge mașina după 5 s ?

Rezolvare:

• Notăm datele problemei și le transformăm în SI:

• Scriem formula accelerației și scoatem necunoscuta, v₂:

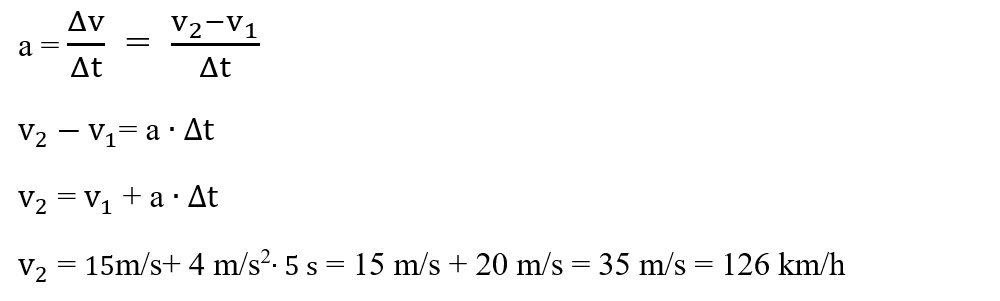
3. Două corpuri pornesc din același punct, pe aceeași direcție cu vitezele inițiale v₀₁ = 4 m/s, respectiv v₀₂ = 2 m/s și accelerațiile a₁ = 2 m/s², respectiv a₂ = 4 m/s². Mobilul 2 pornește mai târziu decât primul la un interval τ = 1 s. Să se afle:
a) După cât timp și la ce distanță se vor întâlni corpurile.
b) Vitezele medii ale mobilelor de la punctul de plecare până când s-au întâlnit.

Rezolvare:

Notăm datele problemei:
v₀₁ = 4 m/s
v₀₂ = 2 m/s
a₁ = 2 m/s²
a₂ = 4 m/s²
τ = 1 s

a)

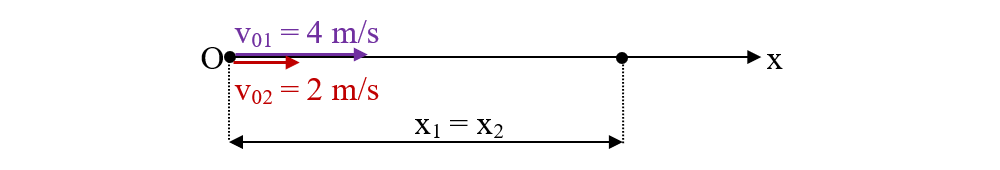
Alegem originea coordonatei (O) în punctul în care se află mobilul 1 la t₀ = 0 și în care pozițiile inițiale ale celor două mobile să fie zero, adică x₀₁ = x₀₂ = 0.

Pentru ca cele 2 corpuri să se întâlnească, ele trebuie să fie în același punct pe axa Ox, la aceeași distanță de origine, adică x₁ = x₂.

Aplicăm legea spațiului în MRUA pentru fiecare mobil, înlocuind datele problemei și apoi egalăm coordonatele:

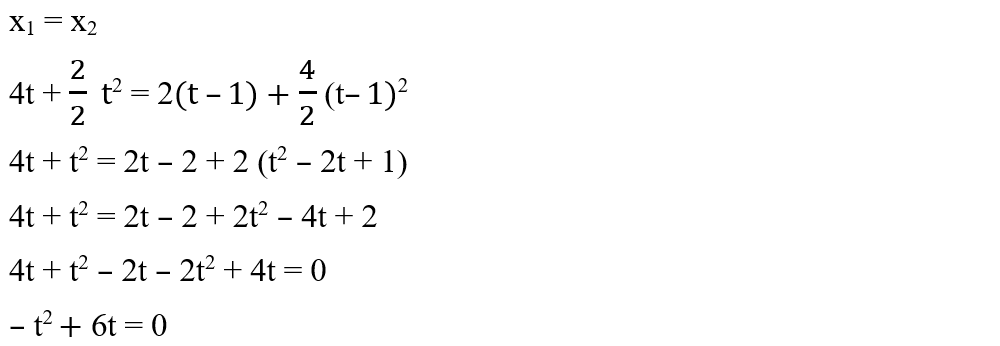
Pentru a afla timpul de întâlnire al celor două mobile de când a plecat primul mobil, trebuie rezolvată ecuația de gradul al doilea:

– t² + 6t = 0

Scriem ecuația generală de gradul al II-lea:

ax² + bx + c = 0

a = –1; b = 6; c = 0

Soluțiile ecuației sunt :

Această soluție este inacceptabilă, deoarece ar însemna că acest corp nu s-a mișcat, rămânând în origine.

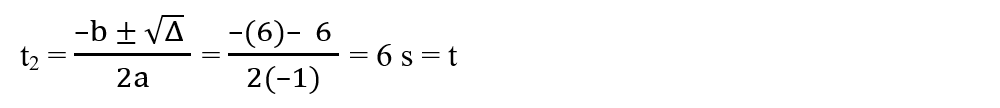
Coordonata punctului de întâlnire este:

b) Calculăm vitezele medii ale celor două mobile:

4. Un mobil care pleacă din repaus se deplasează rectiliniu uniform accelerat cu o accelerație de 0,5 m/s². La poziția x₁ atinge o viteză de 20 m/s și la poziția x₂ viteza lui este 25 m/s. Să se afle:
a) Poziția x₁ față de origine.
b) Timpul în care a ajuns de la origine în poziția x₁.
c) Timpul în care parcurge distanța de la x₁ la x₂.
d) Poziția x₂ față de x₁.
e) Vitezele medii pe porțiunile Ox₁ și x₁x₂.

Rezolvare:

Notăm datele problemei:
v₁ = 20 m/s
v₂ = 25 m/s
a = 0,5 m/s²
x₁ = ?

Pentru a afla poziția unui mobil, știindu-i numai viteza și accelerația în acel punct, aplicăm formula lui Galilei pentru MRUA:

v² = v₀² + 2a (x-x₀)

Avem x₀ = 0, t = 0 și v₀ = 0, deci putem scrie:

b) Aplicăm legea spațiului în MRUA:

c) Pentru a afla poziția x₂ față de x₁, considerăm originea în x₁, viteza inițială v₁ și aplicăm formula lui Galilei:

d) Pentru a afla timpul t₂ în care parcurge distanța de la x₁ la x₂, considerăm originea în x₁, viteza inițială v₁ și aplicăm legea spațiului:

Pentru a afla timpul trebuie rezolvată ecuația de gradul al doilea:

0,25 t₂² + 20t₂ – 225 = 0

Scriem ecuația generală de gradul al II-lea:

ax² + bx + c = 0

a = 0,25; b = 20; c = – 225

Soluțiile ecuației sunt:

Această soluție (t₂) este inacceptabilă, deoarece timpul nu poate fi negativ.

e) Vitezele medii le aflăm cu media aritmetică a celor două viteze, inițială și finală pentru fiecare porțiune:

5. Un mobil are o mișcare rectilinie după următoarea lege: x(t) = 4 – 5t + t² (m) și [t] = s. Se cere:
a) La ce moment se oprește mobilul și în ce poziție ?
b) Realizează graficul mișcării x(t) = f(t).
c) Ce accelerație are mobilul în momentul opririi?

Rezolvare:

a) Pentru a determina timpul de oprire parcurgem următoarele etape:

Se rezolvă ecuația de gradul al II-lea:

t² – 5t + 4 = 0

Scriem ecuația generală de gradul al II-lea:

ax² + bx + c = 0

a = 1; b = –5; c = 4

Soluțiile ecuației sunt:

Pentru a obține timpul minim se face media aritmetică a celor doi timpi obținuți la rezolvarea ecuației:

Pentru a obține poziția minimă corespunzătoare timpului minim, se calculează f(t_min):
f(2,5) = (2,5)² –5(2,5) + 4 = 6,25 –12,5 + 4 = 2,25 m

b)

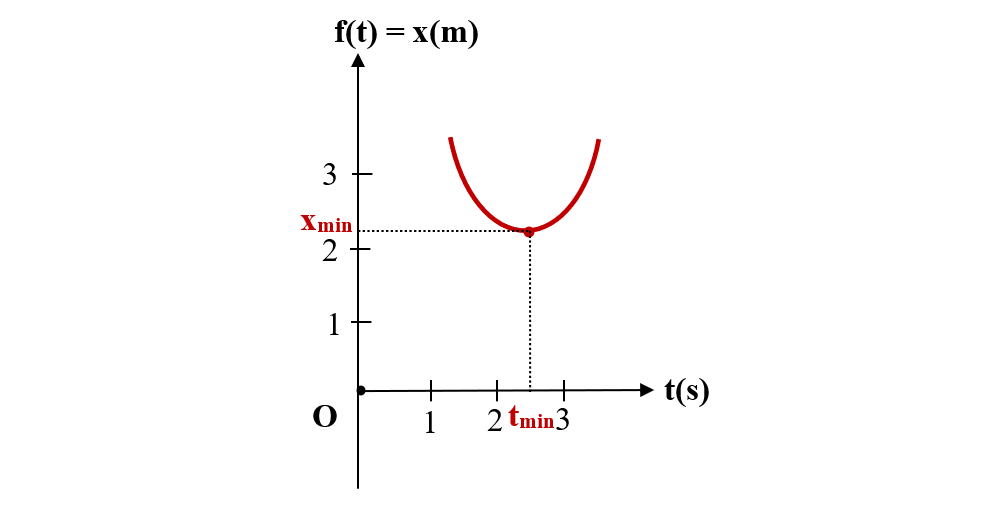
c) Pentru a afla accelerația scriem legea spațiului și o comparăm cu ecuația mișcării:

Termenul liber este coordonata inițială: x₀ = 4 m.

Coeficientul timpului t este viteza inițială: v₀ = – 5 m/s.

Coeficientul timpului la pătrat t² este jumătate din accelerație: a = 2 m/s².

Un mobil are o mișcare rectilinie uniform decelerată atunci când modulul vitezei lui scade în timp.

Iată cum arată pozițiile unui mobil la intervale de timp egale în mișcarea rectilinie uniform decelerată (frânată):

În mișcarea rectilinie uniform decelerată:
- Mobilul parcurge distanțe din ce în ce mai mici, în intervale de timp egale.
- Accelerația momentană este egală cu accelerația medie, fiind constante.
- Accelerația și viteza au aceeași direcție, dar sens opus.

Legea accelerației în MRUD este:

Legea vitezei în MRUD este:

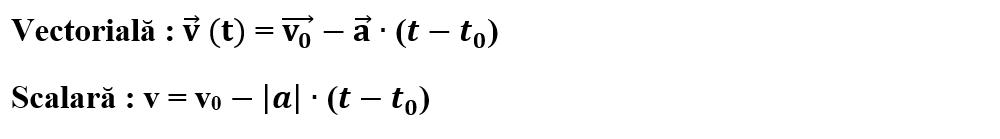
Deoarece în MRUD, în intervalul de timp [t₀, t], viteza mobilului scade liniar cu timpul și la un moment corpul se va opri, având viteza v(t_op)= 0. Acest timp de oprire, notat t_op, se calculează din legea vitezei, cu relația:

Pentru cazul particular, t₀ = 0, timpul de oprire este:

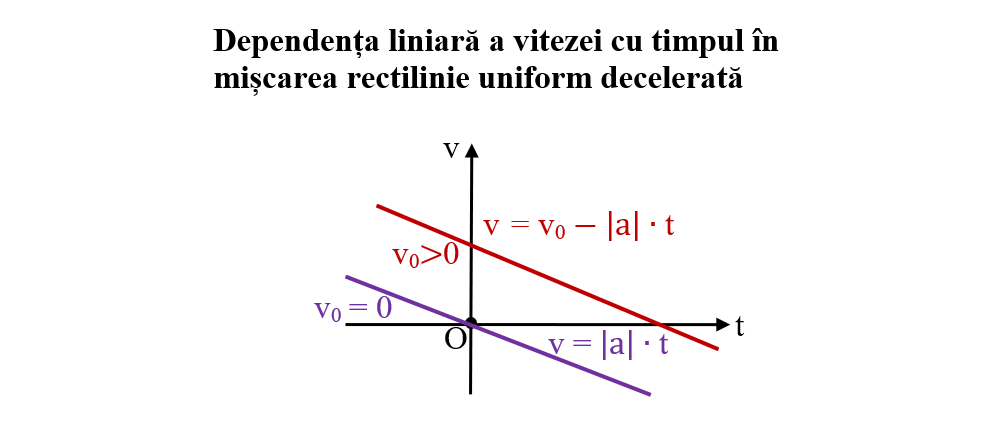
Legea spațiului în MRUD:

Când avem cazul particular t₀ = 0, legea spațiului devine:

Când avem cazul particular t₀ = 0, v₀ = 0 și x₀ = 0, legea spațiului devine:

🔦 Observație

Formula lui Galilei ne permite să calculăm viteza mobilului pentru orice poziție (x) a sa:
v² = v₀² - 2|a| ∙ (x-x₀)

Cazuri particulare:

a) Dacă mobilul pleacă chiar din O (originea coordonatelor), x₀ = 0, la t = 0, atunci avem relația:

v² = v₀² - 2|a|∙x

b) Dacă și v₀ = 0, adică mobilul pleacă din repaus, la t = 0, avem:

v² = 2|a|∙x

🔓 Probleme rezolvate

6. O bilă este aruncată vertical în sus cu o viteză inițială de 2 m/s. Accelerația gravitațională o considerăm constantă, g ≈ 10 m/s² (în mod normal ea scade cu creșterea altitudinii). Să se determine:
a) Timpul în care bila urcă la înălțimea maximă.
b) Înălțimea maximă la care urcă bila.
c) Timpul în care bila coboară de la înălțimea maximă înapoi pe sol.

Rezolvare:

a) Când bila urcă pe verticală, ea are o mișcare rectilinie uniformă decelerată, deoarece se mișcă în sens opus atracției gravitaționale, cu o accelerație |a| = g. Mișcându-se frânat, la un moment dat se va opri la o anumită înălțime. Prin urmare aplicăm formula timpului de oprire din MRUD, cu t₀ = 0:

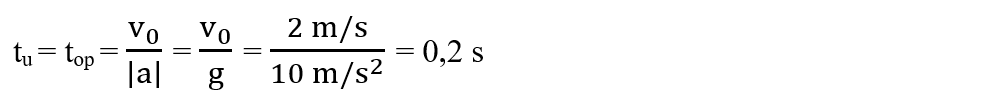
b) Pentru a calcula înălțimea maximă la care urcă bila, cu x₀ =0, aplicăm relația coordonatei de oprire x_op = h_max:

c) Odată ajunsă la înălțimea maximă, bila se va opri și imediat va începe să coboare sub acțiunea accelerației gravitaționale constante, adică va avea o mișcare rectilinie uniformă accelerată. Scriem legea spațială a MRUA:

Când avem cazul particular t₀ = 0, v₀ = 0 și x₀ = 0, legea spațiului devine:

Egalăm cele două formule și scoatem necunoscuta, timpul de coborâre, t_c :

7. Un tren care circulă cu o viteză de 22 m/s se deplasează pe aceeași linie și în același sens cu un alt tren care circulă cu viteza de 18 m/s. Se cere:
a) Cu ce accelerație trebuie să frâneze primul tren pentru a nu se ciocni cu cel de-al doilea tren, știind distanța dintre trenuri de 160 m.
b) Cu ce accelerație trebuie să frâneze primul tren pentru a nu se ciocni cu cel de-al doilea tren, dacă trenurile au sensuri opuse și ambele trenuri vor frâna ? Care este distanța parcursă de primul tren până la oprire ?

Rezolvare :

Datele problemei: v₁ = 22 m/s v₂ = 18 m/s d = 160 m

a) Când trenurile au aceeași direcție și același sens, este suficient numai ca primul tren trebuie să frâneze ca să ajungă la viteza celui de-al doilea tren. Deci, aplicăm formula lui Galilei, luând poziția primului tren egală cu distanța dintre cele două trenuri înainte de a începe frânarea :

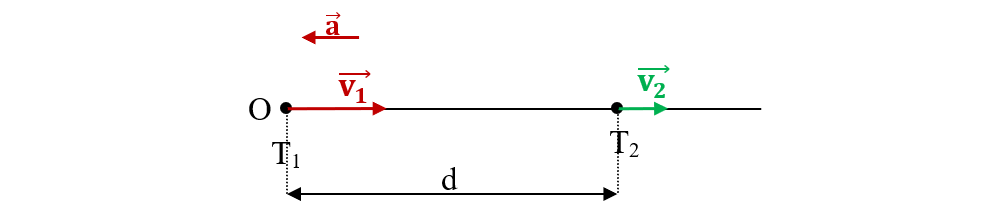
b) Când trenurile au aceeași direcție, dar sens opus, ambele trenuri trebuie să frâneze până la oprire, cu accelerația a. Dar ambele trenuri se mișcă unul spre altul, astfel până la oprire primul tren considerăm că parcurge o distanță x₁, iar cel de-al doilea x₂ = d – x₁. Aplicăm formula lui Galilei pentru ambele trenuri :

Îl înlocuim pe x₁ în cea de-a doua ecuație, pentru a afla necunoscuta a.

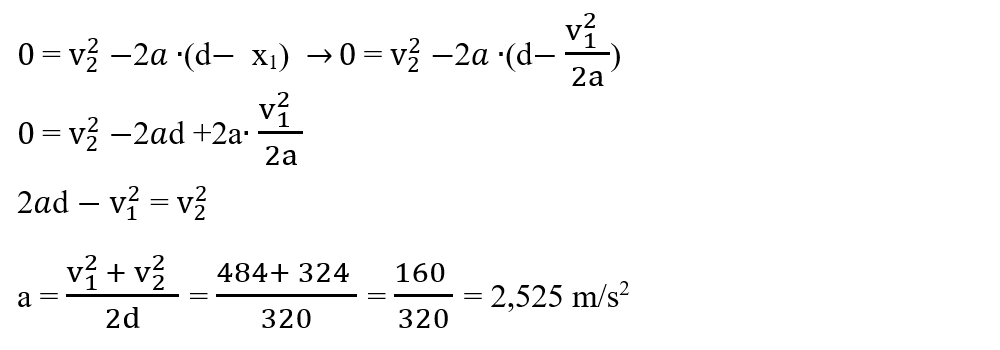
Pentru a determina distanța parcursă de primul tren până la oprire, înlocuim datele obținute:

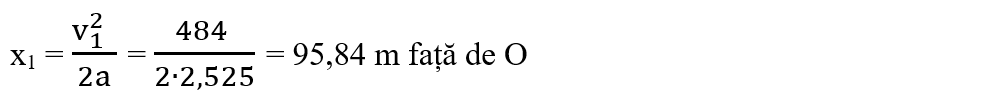
III.1.3.7. Mișcarea circulară uniformă.

Mișcarea circulară este mișcarea unui mobil care are traiectoria un arc de cerc în jurul unei axe.

Mișcarea circulară uniformă (MCU) are loc când viteza punctului material este constantă în modul, adică mobilul descrie arce de cerc egale în intervale de timp egale.

Legea accelerației în MCU este:

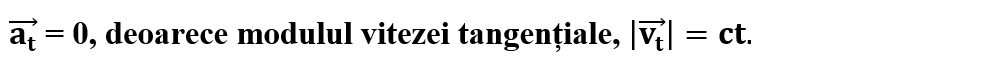
Legea vitezei în MCU este:

Legea spațiului liniar în MCU este:

Mișcarea circulară uniformă se mai poate descrie și prin viteza unghiulară (ω) și spațiul unghiular (α).

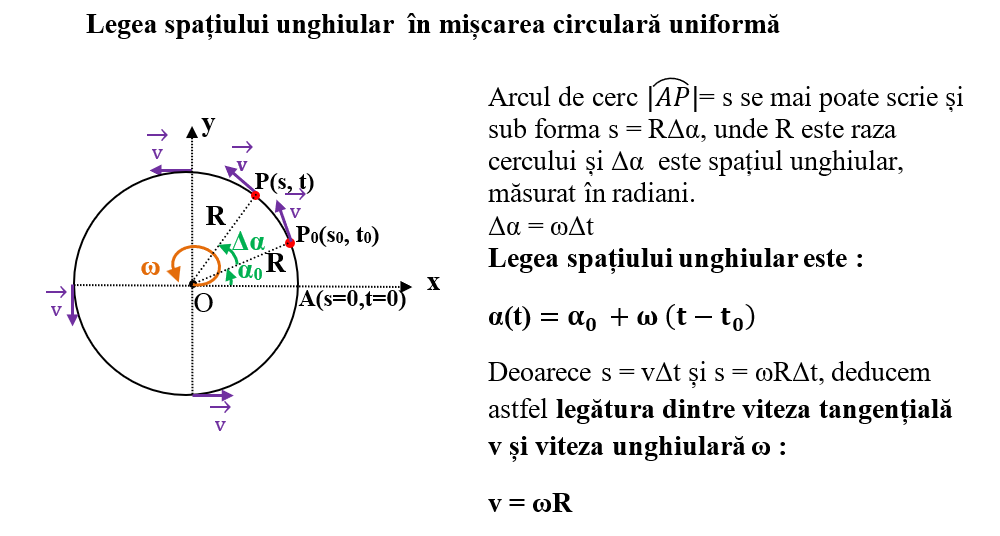
Se observă în figura MCU că, luând OA ca axă de referință, mobilul aflat în P₀ la momentul t₀ este localizat de raza vectoare OP₀, care face unghiul α₀ cu OA.

La momentul t, mobilul ajunge în punctul P, localizat de raza vectoare OP, care face unghiul α cu OA. Deci, mobilul a parcurs spațiul unghiular (numit și unghiul la centru) Δα = α₂ – α₁, în intervalul Δt = t₂ – t₁.

Viteza unghiulară medie (ωm) este spațiul unghiular descris de raza vectoare în unitatea de timp și este dată de relația:

Legea spațiului unghiular este:

α(t)= α₀ + ω(t - t₀)

Cazuri particulare:

când t₀ = 0 și α₀ = 0 (mobilul pleacă din punctul A) avem:

α = ωt

Legătura dintre viteza tangențială v și viteza unghiulară ω:

🔦 Observații importante

Radianul este un unghi la centru care subîntinde un arc de cerc egal cu raza cercului. Cum unghiul total are 360°, el subîntinde toată lungimea cercului care cuprinde 2π raze. Deci, unghiul de 360° are 2π radiani.

1 rad = 360°/ 2π

Viteza unghiulară instantanee (ω) se obține la limita pentru t₂ → t₁ și este dată de relația:

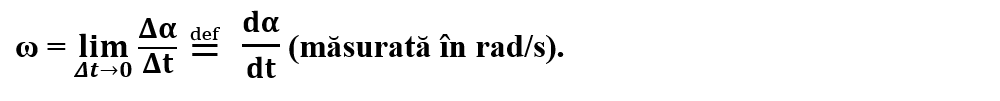
Deoarece mișcarea este uniformă avem **ω_m = ω.

Mișcarea circulară uniformă este o mișcare periodică, deoarece se repetă identic după parcurgerea întregului cerc, la intervale egale.

Perioada mișcării circulare uniforme este intervalul de timp în care mobilul realizează o rotație completă, parcurgând circumferința cercului, de lungime 2πR. În acest interval de timp spațiul unghiular descris de poziția inițială și cea finală este de 2π radiani (360°).Ea se măsoară în secunde.

Frecvența de rotație reprezintă numărul de rotații complete (n) efectuate într-un anumit interval de timp, Δt.

Frecvența se măsoară în s^-1, adică în hertz (Hz).

🔦 Observație

Turația (n) este o frecvență de rotație măsurată în rot/min (1 rot/s = 60 rot/min).

Accelerația centripetă (normală) are expresia:

🔦 Observații

Ecuația vectorială ne dă accelerația centripetă atât ca mărime, cât și ca orientare (direcție și sens):

Viteza tangențială este egală cu produsul vectorial dintre viteza unghiulară (ω) și raza vectoare (R), adică :

Aplicând modulul în ambii membrii ai acestei ecuații, obținem:

Exemple de mișcări circulare uniforme:

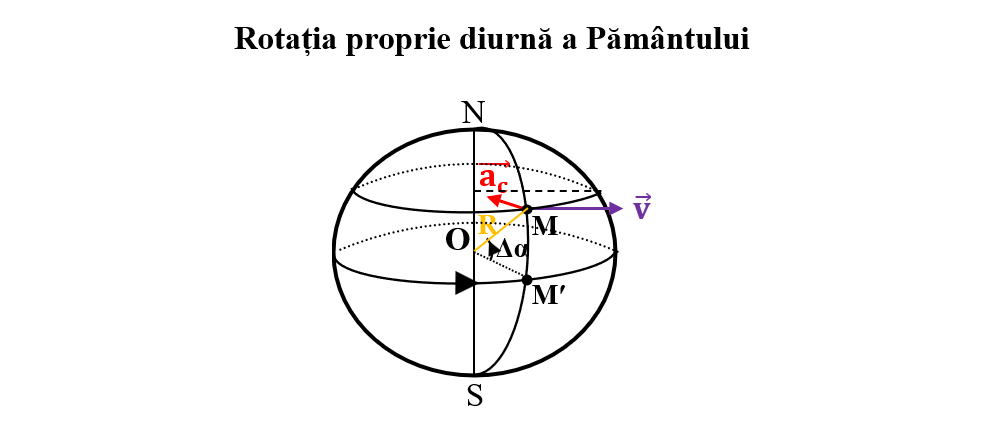
1. Mișcarea proprie de rotație a Pământului în jurul propriei axe, având o perioadă de rotație de aproximativ 24 h. Deoarece raza de la centrul (O) până la suprafața Pământului scade de la ecuator spre cei doi poli, viteza tangențială depinde da latitudine (Pământul este o sferă turtită la poli și bombată la ecuator). Viteza tangențială este maximă la ecuator și scade până la zero la poli. În schimb, viteza unghiulară este aceeași pentru toate punctele de pe suprafața Pământului.

Pământul se rotește spre est. Observat dinspre Steaua Polară, acesta se rotește în sens trigonometric, adică în sens antiorar.

Rotația Pământului în jurul propriei axe duce la schimbarea iluminării solare pe suprafața Pământului de la est la vest, adică la schimbarea zilei și a nopții.

Rotația Pământului în jurul propriei axe a devenit un adevăr incontestabil când fizicianul francez J. Foucault a efectuat faimosul său experiment, cu un imens pendul gravitațional, în Panteonul din Paris, în februarie 1851. Dovezile fizice ale rotației axiale a Pământului sunt măsurate și prin arcul de meridian de 1°, care se află la 110,6 km în apropierea ecuatorului și la 111,7 km în apropierea polilor. Aceste măsurători dovedesc comprimarea Pământului la poli, fiind caracteristică doar corpurilor în rotație.

2. Mișcarea acelor de ceasornic are loc cu perioade diferite. Perioada orarului este de 12 h, cea a minutarului este de 60 min și cea a secundarului de 60 s.

3. Mișcarea roților când se deplasează rectiliniu uniform, astfel încât toate punctele de pe roată se mișcă cu aceeași viteză unghiulară față de punctul de contact dintre roată și sol. În schimb viteza tangențială a punctelor de pe roată depinde de distanța punctului față de centrul roții.

4. Mișcarea roților unui carusel

5. Mișcarea unei elice (a ventilatorului, a morilor de vânt, a elicopterelor etc.), în care toate punctele de pe elice au aceeași viteză unghiulară, dar viteza tangențială a lor diferă în funcție de distanța până la centru de rotație.

6. Mișcarea unui scripete care se deplasează rectiliniu uniform

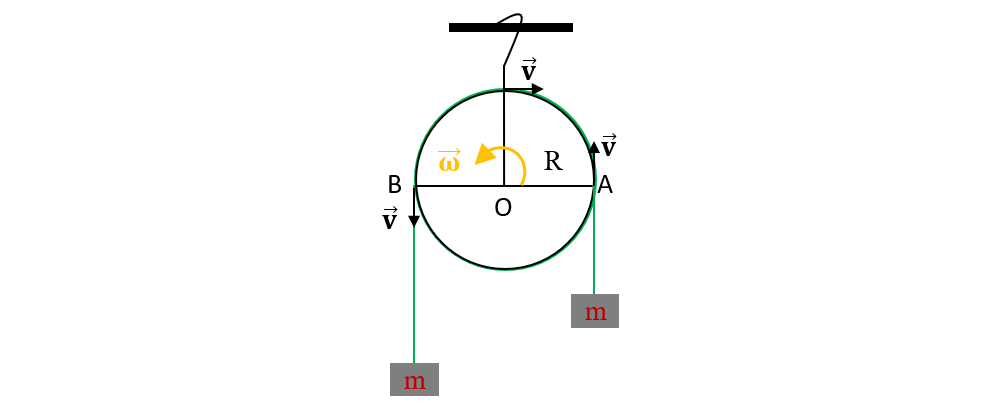
Punctele de pe extremitatea scripetelui au aceeași viteză tangențială (v) și aceeași viteză unghiulară (ω). Dacă R este raza scripetelui, atunci viteză unghiulară este

Legile particulare ale mișcărilor cu t₀ = 0:

🔓 Probleme rezolvate

1. Care este perioada de rotație și viteza unghiulară a acelor unui ceas ?

Rezolvare:

a) Pentru orar avem:

b) Pentru minutar avem:

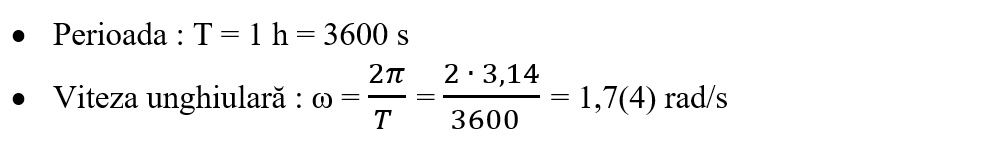
c) Pentru secundar avem:

2. Vârful minutarului unui ceas de perete s-a deplasat cu 1 cm pe cadranul său, într-un minut. Care este lungimea minutarului ?

Rezolvare:

Notăm datele problemei:
Δs = 1 cm = 0,01 m
Δt = 1 min = 60 s
T = 3600 s
R = ? (considerăm că lungimea acului minutar este egală cu raza ceasului)

Știm că lungimea cercului (2πR) este egală cu viteza tangențială (v) a acului înmulțită cu perioada de rotație (T) a acului minutar, adică:
2πR = v ∙ T

De asemenea viteza acului este:

Înlocuim viteza în relația: 2πR = v ∙ T și obținem:

Scoatem necunoscuta R, care este chiar lungimea minutarului:

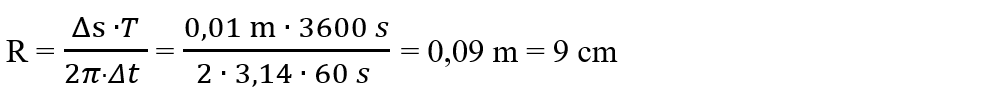
3. Se dă următorul tabel cu date despre timpul la care un punct material se deplasează circular uniform și spațiul unghiular corespunzător:

Se cere :
a) Realizează graficul dependenței spațiul unghiular în radiani în funcție de timp.
b) Determină legea spațiului unghiular.
c) Viteza unghiulară.
d) Frecvența de rotație.
e) Perioada rotației.

Rezolvare:

a) Transformăm spațiile unghiulare (luate din tabel) din grade în radiani:

Realizăm graficul dependenței spațiul unghiular în radiani în funcție de timp:

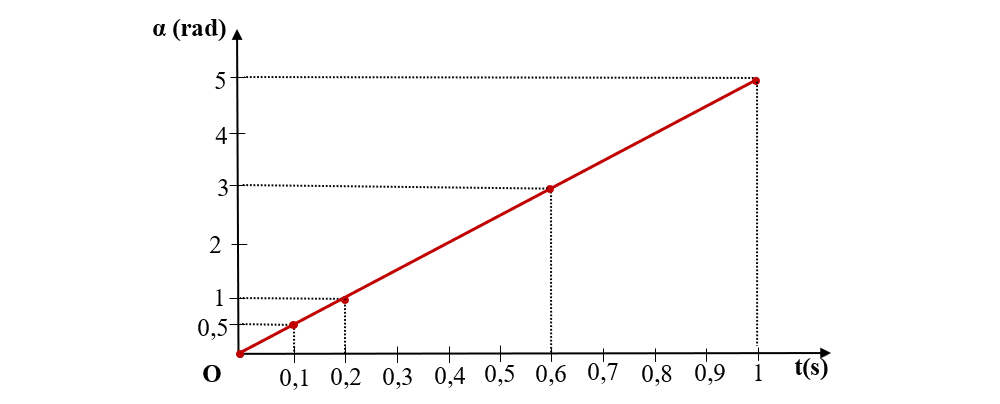
b) Pentru a determina legea spațiului unghiular, pe graficul realizat la punctul a, de la unitatea timpului (1 s) ducem o dreaptă paralelă cu axa spațiului unghiular până întâlnim linia graficului și din acel punct ducem o dreaptă paralelă cu axa timpului până ne intersectăm cu axa spațiului. Observăm că la 1 s avem un spațiu unghiular de 5 rad.

Cum α = f(t) este o linie dreaptă, obținem legea spațiului unghiular :
α = 5t

c) Aplicăm formula vitezei unghiulare în funcție de spațiul unghiular și timp:

d) Frecvența de rotație este:

e) Perioada de rotație este:

4. O mașină de formula 1 cu viteza constantă în modul de 216 km/h se antrenează pe o pistă circulară cu raza de 100 m.

Se cere:
a) Viteza unghiulară a mașinii.
b) Perioada mișcării circulare uniforme.
c) Știind că diametrul roților este de 0,5 m, cât este frecvența de rotație a roților sale ?

Rezolvare:

Notăm datele problemei:
v = 216 km/h = 216/3,6 = 60 m/s
R = 100 m
D = 0,5 m (diametrul roții)
ω₁ = ? (a mașinii)
T = ?
ν₂ = ? (a roților mașinii)

a)

b)

c)

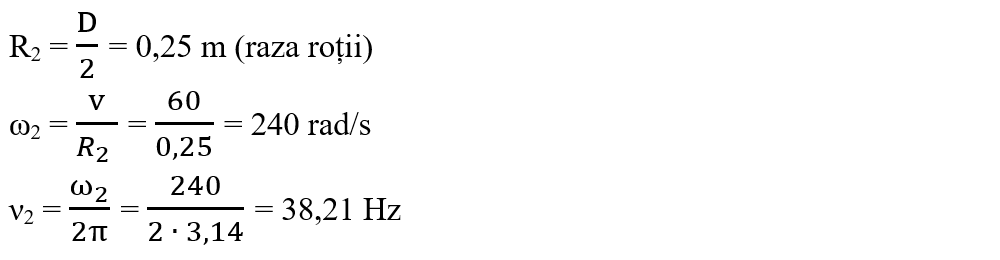
5. O mașină face un viraj de 90°, având o rază de 10 m într-un interval de timp de 1 s. Calculează viteza tangențială a mașinii.

Rezolvare:

Notăm datele problemei:

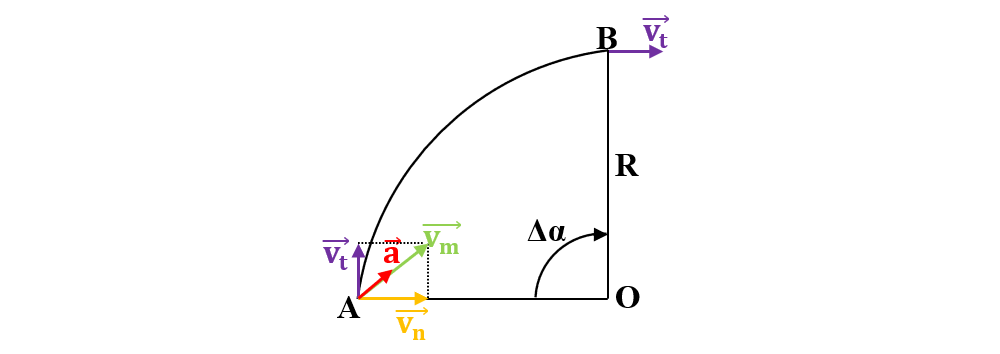
6. Calculează viteza unghiulară de rotație a Pământului, viteza liniară și accelerația centripetă a unui punct material de pe suprafața Pământului la latitudinea de 45°. Știm că Pământul efectuează o rotație completă la fiecare 23 h și 56 min și raza Pământului este de 6371 km.

Rezolvare:

Notăm datele problemei:
T = 23 h + 56 min = 23 ∙ 3600 s + 56 ∙ 60 s
T = 82800 s + 3360 s = 86160 s
Δα = 45°
R = 6371 km = 6371000 m
ω =?
v = ?
a_c = ?

a)

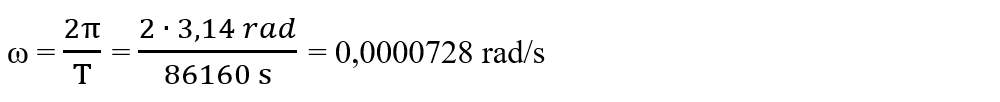
b)

c)