III.1.2. Elemente de calcul vectorial.
- III.1.2.1. Mărimi scalare și mărimi vectoriale.
- III.1.2.2. Clasificarea vectorilor.
- III.1.2.3. Operații cu vectori.
III.1.2.1. Mărimi scalare și mărimi vectoriale.
Mărimile fizice sunt de două feluri: scalare și vectoriale.
Mărimea fizică scalară (pe scurt, scalar) este mărimea care se caracterizează complet prin:
- Valoare numerică
- Unitate de măsură.
Marea majoritate a mărimilor fizice sunt scalare: lungimea, aria, volumul, timpul, masa, densitatea, temperatura, intensitatea curentului electric, tensiunea electrică etc.
Ele se pot aduna ca orice numere.
Mărimea fizică vectorială (pe scurt, vector) este mărimea care se caracterizează complet prin:
- Valoare numerică (modul)
- Unitate de măsură
- Orientare (direcție și sens).
Pentru a diferenția un scalar de un vector, mărimii vectoriale i se pune deasupra simbolului, o săgetuță.
Mărimile vectoriale studiate în gimnaziu sunt:

III.1.2.2. Clasificarea vectorilor.



Clasificarea vectorilor în funcţie de punctul lor de aplicaţie:
- Vectori liberi, la care punctul de aplicaţie poate ocupa orice poziţie în spaţiu, menţinându-se aceleaşi: mărimea, direcţia şi sensul, fără ca efectul vectorului să se modifice. Aceşti vectori se caracterizează prin modul, direcţie şi sens (exemple: vitezele şi acceleraţiile unui corp în mişcarea de translaţie, momentul unui cuplu de forţe.)
- Vectori alunecători (glisanți), la care punctul de aplicaţie se poate deplasa numai pe suportul vectorului, menţinându-se acelaşi modul şi sensul vectorului. Aceşti vectori se caracteriză prin modul, direcţie, sens şi dreapta suport (exemple: forţele aplicate unui corp rigid).
- Vectori legaţi (ficși), la care punctul de aplicaţie este bine determinat. Aceşti vectori se caracterizează prin modul, direcţie, sens şi punct de aplicaţie (exemple: momentul unei forţe în raport cu un punct).
III.1.2.3. Operații cu vectori.
1. Înmulțirea unui vector cu un scalar.

-
Vectorul obținut păstrează direcția și sensul primului vector în cazul în care numărul real a > 0.
-
În cazul în care numărul real a < 0, vectorul obținut păstrează direcția inițială, dar va avea sens opus vectorului inițial.
Exemplu:

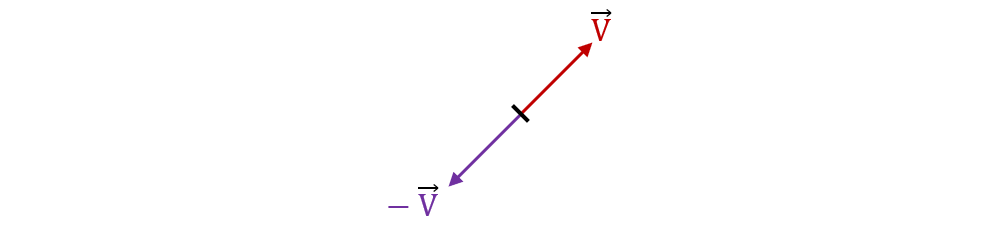
🔦 Observație importantă:

2. Adunarea (compunerea) vectorilor.

Pentru a compune 2 vectori concurenți aplicăm regula paralelogramului, parcurgând următoarele etape:
- Se desenează ce doi vectori astfel încât să aibă același punct de aplicație.
- Cu segmentele celor 2 vectori, se formează un paralelogram (patrulater cu laturile paralele și egale).
- Se trasează diagonala paralelogramului care are punct comun cu cei doi vectori. Acest segment reprezintă vectorul rezultant, care se notează și i se pune săgeată în capăt.
Modulul vectorului sumă este dat de relația:
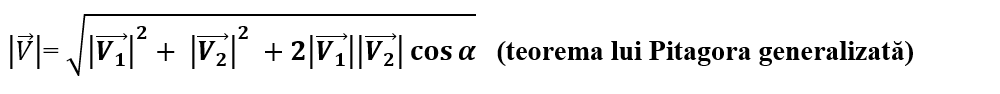
🔦 Observație


🔓 Problemă rezolvată
1. Un râu curge spre est cu o viteză de 60 km/h. O barcă merge pe râu în sensul lui de curgere cu viteza de 100 km/h , pe o direcție ce face un unghi de 30° față de malul râului. Care este viteza bărcii față de mal?
Reprezintă grafic la scara : 1cm:20 km/h.
Rezolvare:
Scriem datele problemei
v1 = 60 km/h, direcție orizontală, sensul spre dreapta
v2 = 100 km/h, direcție ce face un unghi de 30° cu orizontala, în sus.
1cm : 20 km/h
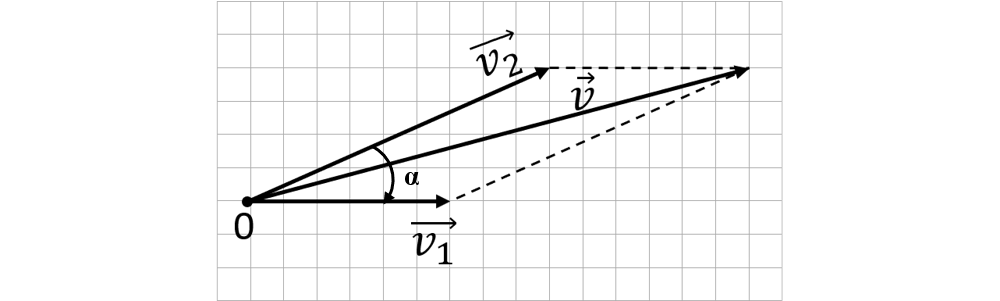
Modulul vectorului sumă este dat de relația:
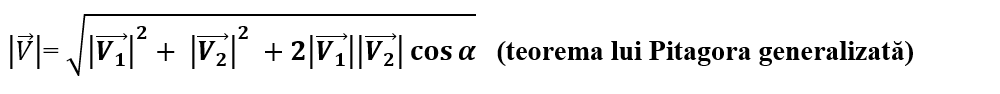
v2 = v12+ v22 + 2v1 • v2 • cosα = 602 + 1002 + 2 ∙ 60 ∙ 100 ∙ cos 30°
v2 = 3600 + 10000 + 12000 ∙ 1/2
v2 = 19600
v = 140 km/h
Când cei doi vectori sunt coliniari (au aceeași direcție), avem două cazuri particulare la regula paralelogramului:
a) Când cei doi vectori sunt coliniari și cu același sens (unghiul dintre ei este de 0°), vectorul rezultant are:
- valoarea numerică egală cu suma valorilor numerice a vectorilor componenți
- direcția comună cu vectorii componenți
- sensul comun cu vectorii componenți.
b) Când cei doi vectori sunt coliniari și cu sensuri opuse (unghiul dintre ei este de 180°), vectorul rezultant are:
- valoarea numerică egală cu diferența valorilor numerice a vectorilor componenți (se scade din cel cu valoarea mai mare cel cu valoare mai mică)
- direcția comună cu vectorii componenți
- sensul vectorului cu valoare mai mare.
🔓 Probleme rezolvate
2. Doi copii trag de o sanie pe un drum orizontal, spre vest, cu forțele F1 = 400 N, respectiv F2 = 800 N. Compune cele două forțe ale copiilor.
Rezolvare:
Vectorul rezultant are:
- valoarea numerică egală cu suma valorilor numerice a vectorilor componenți, adică F = F1 + F2 = 400 N + 800 N = 1200 N
- direcția comună cu vectorii componenți: orizontală
- sensul comun cu vectorii componenți: spre stânga.
Pentru a reprezenta vectorul rezultant trebuie să ne alegem un etalon corespunzător, astfel încât să avem loc de desen pe pagina caietului.
Etalon: 1 cm : 200 N
Segmentul vectorului rezultant este de 1200:200 = 6 cm.

3. Asupra resortului unui dinamometru suspendat de un suport, acționează două forțe, una de 60 N, pe verticală în jos, cealaltă de 150 N, pe verticală în sus. Ce forță indică dinamometrul ?
Rezolvare:
Vectorul rezultant are:
- valoarea numerică egală cu diferența valorilor numerice a vectorilor componenți, adică F = F2 – F1 = 150 N – 60 N = 90 N
- direcția comună cu vectorii componenți: verticală
- sensul vectorului cu valoare mai mare: în sus.
Pentru a reprezenta vectorul rezultant trebuie să ne alegem un etalon corespunzător, astfel încât să avem loc de desen pe pagina caietului.
Etalon: 1 cm : 30 N.
Segmentul vectorului rezultant este de 90:30 = 3 cm.

Pentru adunarea a mai multor vectori necoliniari neconcurenți (care nu au același punct de aplicație) se folosește regula poligonului, parcurgând următoarele etape :
- Se desenează primul vector.
- Al doilea vector se desenează cu originea în vârful primului vector, păstrându-i direcția.
- Al treilea vector se desenează cu originea în vârful celui de-al doilea vector, păstrându-i direcția ș.a.m.d. până reprezentăm toți vectorii.
- Vectorul rezultant este segmentul care se obține prin unirea originii (0) cu vârful ultimului vector, având vârful în vârful ultimului vector.
- Valoarea vectorului rezultant o obținem prin măsurarea segmentului său cu rigla și apoi înmulțim cu etalonul dat (ales).
Observație:
Regula triunghiului este un caz particular al regulii poligonului pentru 2 vectori.
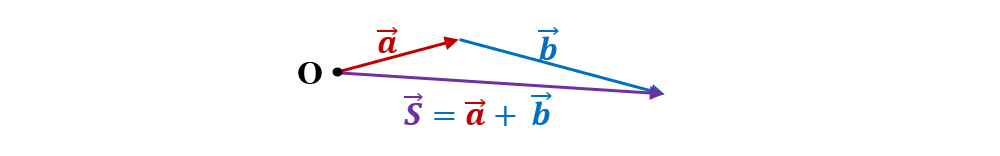
🔓 Problemă rezolvată
4. Un biciclist merge către est 20 km, apoi către sud 40 km, apoi către vest 80 km și către nord 60 km. Determină vectorul rezultant, adică la ce distanță a ajuns biciclistul față de reper (0).
Rezolvare:
d1 = 20 km, direcție orizontală, spre dreapta
d2 = 40 km, direcție verticală, în jos
d3 = 80 km, direcție orizontală, spre stânga
d4 = 60 km, direcție verticală, în sus

Etalon: 1 cm : 10 km.
-
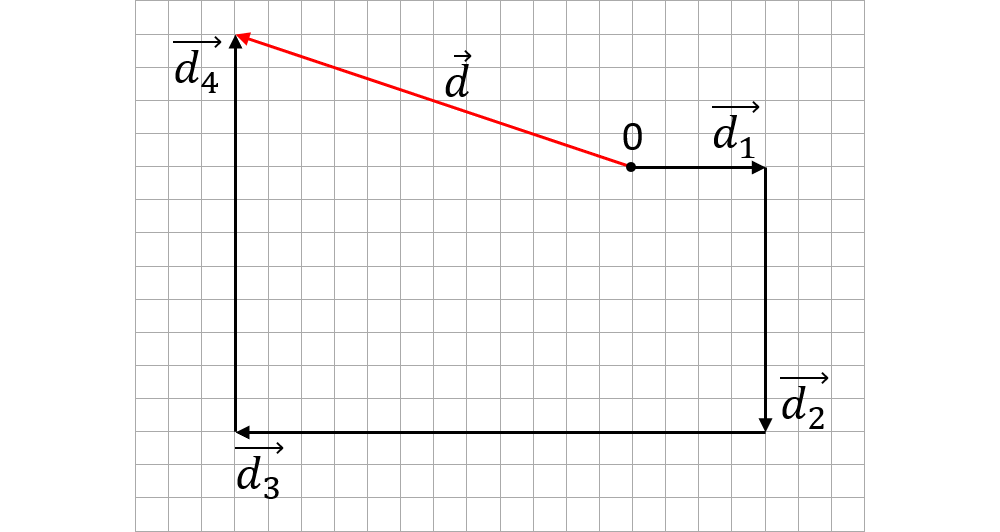
Reprezentăm primul vector deplasare d1. Al II-lea vector îi punem punctul de aplicație în vârful primului, ș.a.m.d. până reprezentăm toți cei patru vectori.
-
Vectorul rezultant este segmentul care se obține prin unirea originii (0) cu vârful ultimului vector, având vârful în vârful ultimului vector.
-
Valoarea vectorului rezultant o obținem prin măsurarea segmentului său cu rigla și apoi înmulțim cu etalonul dat: d = 6,3 ∙ 10 = 63 km. Deci biciclistul se află la o distanță de 63 km față de punctul de plecare, după toată cursa.
3. Descompunerea și proiecția unui vector
Descompunerea unui vector după două direcții reciproc perpendiculare se realizează astfel:
- Din vârful vectorului dat se duc perpendiculare pe cele două direcții Ox și Oy.
- Scriem ecuația vectorială:

- Scriem ecuația scalară:
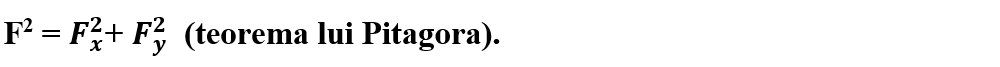

🔦 Observație
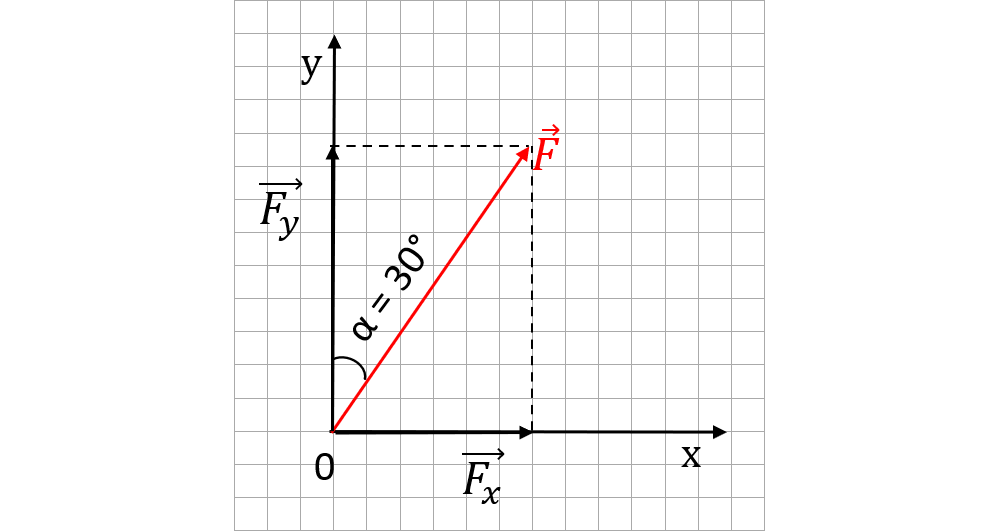
Descompunerea unui vector după două direcții reciproc perpendiculare este inversă compunerii a doi vectori necoliniari și concurenți, cu regula paralelogramului, cu precizarea că vectorii componenți sunt pe cele două direcții principale: Fx pe orizontală și Fy pe verticală. Astfel obținem un dreptunghi care are ca laturi segmentele forțelor componente.
🔓 Problemă rezolvată
5. Laurențiu bate un cui cu ciocanul cu o forță de 500 N într-un perete, ținând cuiul înclinat față de perete cu un unghi α = 30°. Ce valoare au forțele care compun forța lui Laurențiu ?
Rezolvare:
Etalon: 1 cm : 100 N
Desenăm segmentul forței F pe direcția oblică, ce face un unghi de 30° cu verticala. Descompunem forța F ducând din vârful vectorului F perpendiculare pe cele două direcții Ox și Oy.
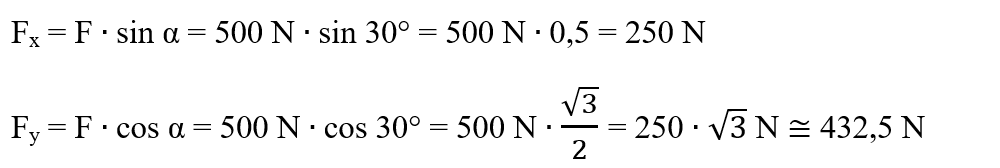
Scriem ecuația vectorială:

Verificăm cu teorema lui Pitagora
Scriem ecuația scalară:
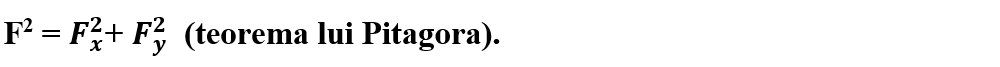
Verificăm rezultatele prin aplicarea teoremei lui Pitagora:

4. Scăderea (diferența) a doi vectori

Vectorul diferență se obține tot cu regula paralelogramului, trasând diagonala mică a acestuia, adică diagonala care unește extremitățile celor doi vectori. Sensul vectorului diferență este de la vectorul scăzător la vectorul descăzut.
Modulul vectorului diferență este dat de relația:
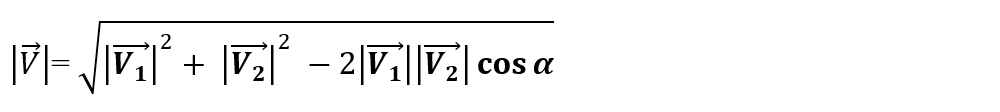
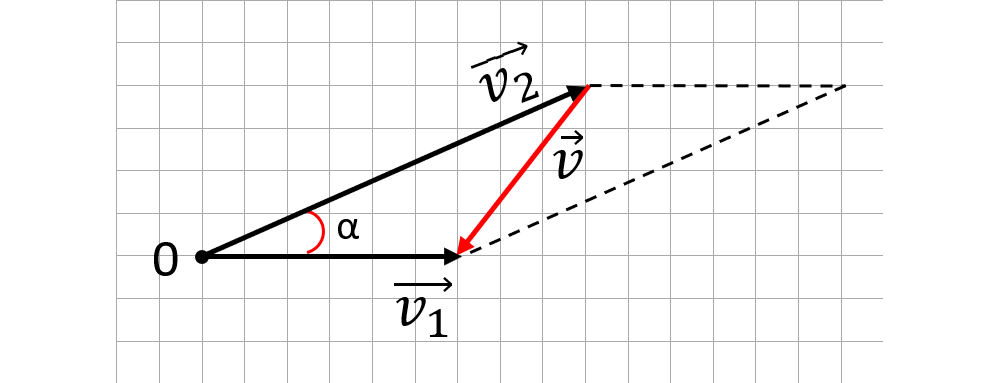
🔦 Observație

🔓 Probleme rezolvate
6. Două mobile se mișcă pe aceeași direcție și același sens cu vitezele v1 = 80 km/h și respectiv v2 = 60 km/h, ambele față de același SR. Calculează viteza relativă (v12) a mobilului 1 față de mobilul 2.
Rezolvare:
Deoarece cele 2 mobile se deplasează pe aceeași direcție și în același sens față de același SR, unghiul α = 0° și viteza relativă a mobilului 1 față de mobilul 2 este dată de vectorul diferență:
v12 = v1 - v2 = 80 km/h – 60 km/h = 20 km/h
2. Două mobile se mișcă pe aceeași direcție, dar în sens opus cu vitezele v1 = 80 km/h și respectiv v2 = 60 km/h, ambele față de același SR. Calculează viteza relativă (v12) a mobilului 1 față de mobilul 2.
Rezolvare:
Deoarece cele 2 mobile se deplasează pe aceeași direcție și în același sens față de același SR, unghiul α = 180° și viteza relativă a mobilului 1 față de mobilul 2 este dată de vectorul diferență :
v12 = v1 – (–v2) = 80 km/h + 60 km/h = 140 km/h
5. Produsul scalar a doi vectori

🔦 Observații
a) Dacă produsul scalar este nul și modulele celor doi vectori sunt diferite de 0, rezultă că cei doi vectori sunt perpendiculari (ortogonali) și reciproc.
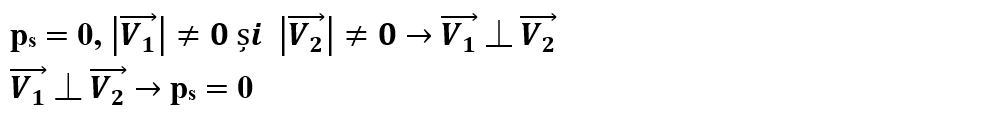
b) Când cei doi vectori au aceeași direcție și același sens, cos α = 1 și produsul scalar este maxim:
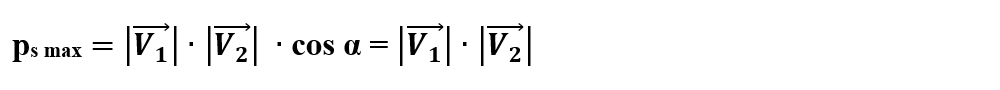
c) Când cei doi vectori au aceeași direcție, dar sens opus, cos α = -1 și produsul scalar este minim :

d) Produsul scalar a 2 vectori este comutativ:

Exemplu de produs scalar
Există mărimi fizice scalare care reprezintă produsul scalar a doi vectori de naturi diferite.

6. Produsul vectorial a doi vectori

Modulul produsului vectorial este dat de relația:

Direcția produsului vectorial este perpendiculară pe planul determinat de cei doi vectori, în punctul lor de concurență (O), adică


🔦 Observații
a) Produsul vectorial este anticomutativ:

b) Produsul vectorial este distributiv față de adunare:

Modulul produsului vectorial este egal cu aria paralelogramului construit cu segmentele celor 2 vectori, adică:


Exemplu de produs vectorial
Să presupunem că un corp solid se rotește în jurul unui punct fix, numit pol (sau articulație), sub acțiunea unei forțe.

Vectorul moment al forței are următoarele caracteristici:

