III.5.1. Forța elastică.

O forță ce acționează asupra unui corp care nu se poate deplasa (care este fixat de un suport) produce corpului o deformare.

În funcție de proprietățile elastice/plastice ale corpului, forța respectivă produce fie o deformare elastică (corpul revine la forma inițială), fie o deformare plastică (corpul nu mai revine la forma inițială).

Un resort alungit sau comprimat este deformat elastic cu o anumită forță, numită forță deformatoare (F).

Când încetează acțiunea asupra lui, resortul revine la forma inițială datorită forței elastice (F_e).

În cele ce urmează vom studia deformările elastice ale corpurilor perfect elastice (care revin într-un timp extrem de scurt la forma inițială), omogene (sunt alcătuite dintr-un anumit material), izotrope (care au aceleași proprietăți fizice pe toate direcțiile) și unilaterale (la care predomină o singură dimensiune).

Este cazul resorturilor, barelor și firelor.

🔦 Observație

Când aplicăm o forță deformatoare unui corp elastic, la nivel microscopic, se măresc distanțele dintre particule corpului. În acest caz forțele de atracție intermoleculare se opun deplasării particulelor, având ca rezultat apariția forței elastice în corpul deformat elastic. În limitele elasticității materialului respectiv, forța elastică apărută este cu atât mai mare, cu cât forța deformatoare este mai mare.

Forța elastică (notată Fe) este forța care apare în interiorul unui corp deformat elastic și readuce corpul la forma inițială, fiind egală, dar de sens opus cu forța deformatoare (F).

Importanța forței elastice care apare în corpurile elastice:

1. Aerul are proprietăți elastice, fiind folosit la pneurile roților pentru amortizarea șocurilor sau la diferite obiecte pneumatice (saltele, mingii, baloane etc.)

2. Arcurile (resorturile) sunt folosite pentru amortizarea șocurilor și vibrațiilor (suspensii de autovehicule, pentru acumulare de energie (arcuri de ceas, rulouri, arcuri de supape), exercitarea unei forţe elastice permanente (cuplaje de siguranţă) , reglarea sau limitarea forţelor sau a debitelor (prese, cuplaje de siguranţă, robinete de reglare etc.).

Resorturile se găsesc în construcția multor obiecte :

• Dinamometre și cântare

• Pulverizatoare

• Pixuri

• Vagoane de tren

• Ceasuri

• Suspensia vehiculului

• Saltea de pat

• Clip de păr

• Clanță și broască de ușă

• Arcuri pentru dulapuri

• Extensor si flexor fitness

• Şaua bicicletei sau motocicletei este aşezată pe arcuri, pentru atenuarea zdruncinărilor în timpul mersului

3. Arc cu săgeți sau arbaletă pentru vânătoare.

4. Coarda elastică în bungee jumping

👀 Experiment: Cum se determină constanta elastică?

Materiale necesare:
Dinamometru, disc cu mase marcate, riglă.

Observaţie

Greutatea corpului suspendat este forța deformatoare, egală în modul cu forța elastică (au aceeași valoare numerică): |G₁ | = |F₁ | = |F_e1 |.

Descrierea experimentului:

• Suspendă dinamometrul pe un suport.
• Măsoară lungimea inițială a resortului dinamometrului: L₀ = 2 cm.
• Suspendă de cârligul dinamometrului un corp și măsoară-i greutatea G₁ = F_e1 = 0,12 N.
• Măsoară lungimea resortului dinamometrului deformat: L₁ = 3,2 cm.
• Calculează alungirea (deformarea) resortului : ΔL₁ = L₁ - L₀ = 1,2 cm.
• Mai repetă aceleași operații pentru încă cel puțin un corp de masă diferită față de primul. Trece datele experimentale în următorul tabel:

Observaţie

Raportul F_e / ΔL este constant pentru un resort dat.

Concluzia experimentului:
Cu cât greutatea corpului suspendat crește, cu atât crește și alungirea resortului. Deci forța elastică este direct proporțională cu deformarea resortului.

Constanta elastică a unui resort (k) este egală cu raportul dintre forța elastică (F_e) și deformarea resortului (ΔL).

[k]_SI = N/m

Legea deformării elastice :

| F | = | F_e | = k ∙ Δl

Legea deformării elastice ne arată că forța deformatoare (F) este egală în modul cu forța elastică (F_e), fiind direct proporțională cu deformarea resortului (Δl). Fiecare resort are o anumită constantă elastică (k), care se determină experimental.

🔓 Probleme rezolvate

1. Un resort are lungimea inițială de 8 cm, iar deformat are lungimea de 3 cm. Știind forța elastică de 400 N, se cere :

a) Constanta elastică a resortului.

b) Tipul deformării.

c) Reprezentarea forței deformatoare și a forței elastice folosind ca etalon

1 cm : 200 N.

Rezolvare

Scriem datele problemei:

l₁ = 8 cm

l₂ = 3 cm

F_e = 400 N

a) Scriem legea deformării elastice, calculăm deformarea Δl și scoatem necunoscuta k:

b) Tipul deformării: comprimare, deoarece l₂ < l₁.

c) 1 cm : 200 N

400 : 200 = 2 cm au segmentele celor două forțe egale în modul, dar de sens opus.

2. Un resort este deformat cu 5 dm de o forță de 3000 N.

a) Cât este forța care deformează același resort cu 900 mm ?

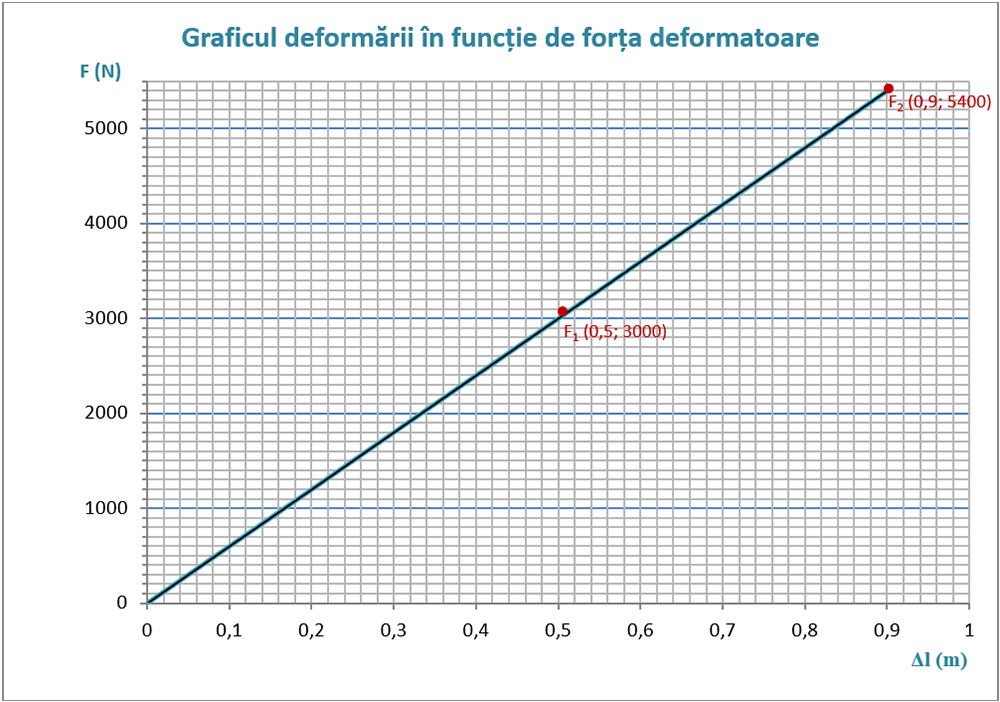
b) Reprezintă graficul deformării în funcție de forța deformatoare, folosind ca etaloane:

• pentru axa forței 1 cm : 1000 N și

• pentru axa deformării 1 cm : 0,1 m.

Rezolvare

Scriem datele problemei și le transformăm în SI:

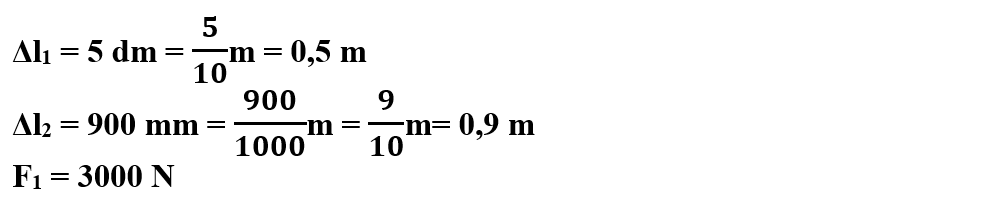
a) Scriem legea deformării elastice pentru prima forță deformatoare și scoatem necunoscuta k:

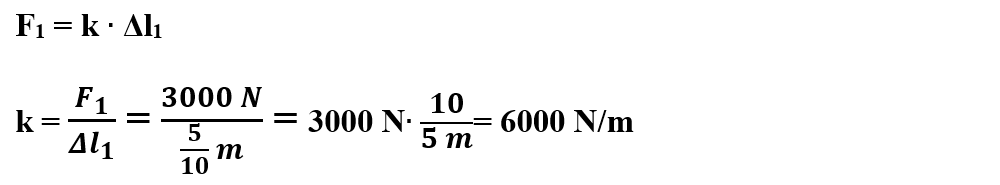
Scriem legea deformării elastice pentru a doua forță deformatoare și scoatem necunoscuta F₂:

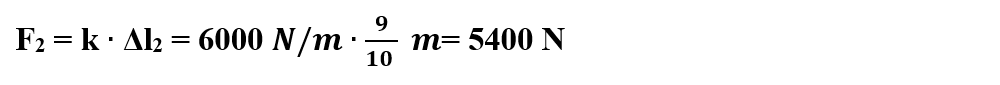
b)

3. Două resorturi de constante elastice 12,5 N/m, respectiv 20 N/m sunt legate în serie. Determină constanta elastică a acestui sistem serie de resorturi.

Rezolvare:

Considerăm că aceeași forță deformatoare F produce fiecărui resort o deformare Δl₁, respectiv Δl₂.
F = k₁ ∙ Δl₁
F = k₂ ∙ Δl₂

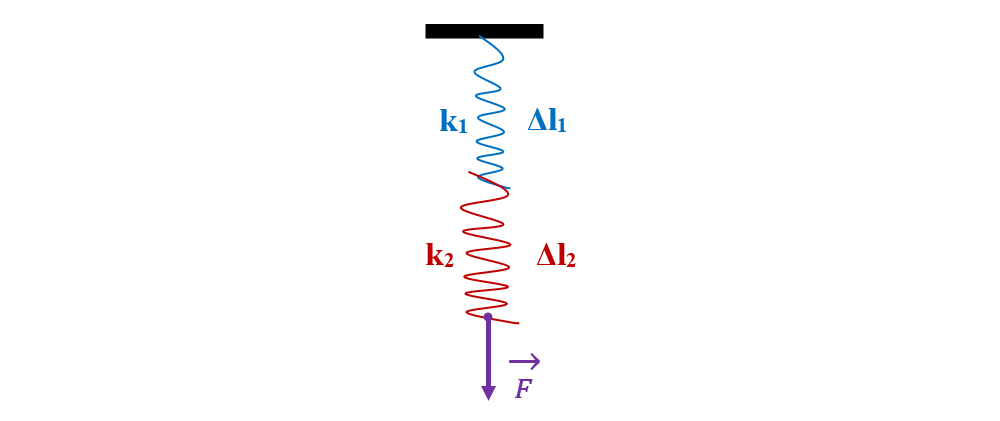
Când aplicăm aceeași forță sistemului serie de resorturi, aceasta va produce o deformare totală:
Δl = Δl₁ + Δl₂

Din ecuațiile legii deformării elastice, scoatem deformările și le înlocuim în ecuația deformării totale:

Înlocuim datele în formula obținută:

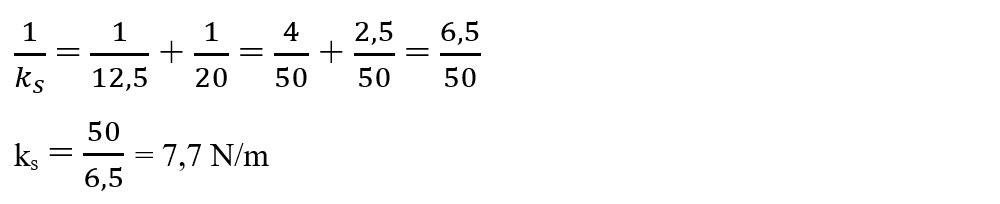
4. Două resorturi de constante elastice 12,5 N/m, respectiv 20 N/m sunt legate în paralel. Determină constanta elastică a acestui sistem paralel de resorturi.

Rezolvare:

Considerăm că forța deformatoare F produce aceeași deformare Δl fiecărui resort și că această forță este suma celor două forțe care acționează asupra fiecărui resort.

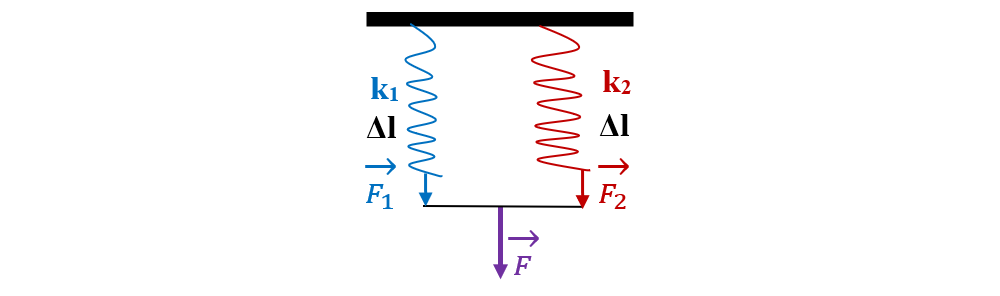
F = F₁ + F₂
F = k_p ∙ Δl
F₁ = k₁ ∙ Δl
F₂ = k₂ ∙ Δl
k_p ∙ Δl = k₁ ∙ Δl + k₂ ∙ Δl
k_p = k₁ + k₂
k_p = k₁ + k₂ = 12,5 N/m + 20 N/m = 32,5 N/m