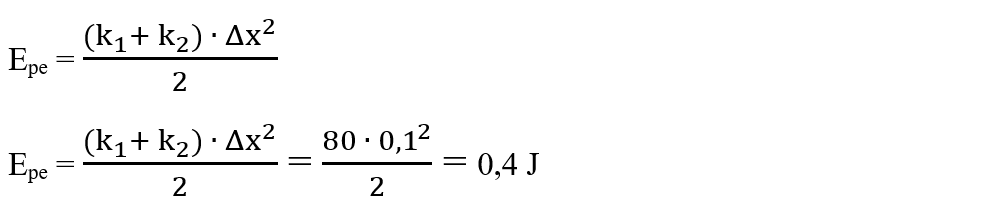IV.4.4. Energia potențială elastică.
👀 Experiment: Energia potențială elastică
Materiale necesare:
O sticlă de plastic cu puțină apă, elastic.
Descrierea experimentului:
- Prinde elasticul de gâtul sticlei.
- Așază sticla pe podea, ținând de capătul elasticului.
- Blochează sticla între tălpile picioarelor.
- Trage de elastic ca să îl întinzi.
- Eliberează sticla.
- Ce observi ?
Sticla urcă la o anumită înălțime.
Concluzia experimentului:
Forța elastică apărută în elasticul alungit efectuează un lucru mecanic asupra sticlei, deplasând-o. Deci elasticul întins posedă energie, numită energie potențială elastică.
👀 Experiment: Un resort cu energie
Materiale necesare:
2 resorturi de dimensiuni diferite, bilă, riglă.
Descrierea experimentului:
- Fixează resortul mai mic și comprimă-l.
- Așază în fața resortului comprimat o bilă.
- Dă drumul la resort. Măsoară distanța parcursă de bilă: d1 =
- Fixează resortul mai mare de masă și comprimă-l.
- Așază în fața resortului comprimat bila.
- Dă drumul la resort. Măsoară distanța parcursă de bilă: d2 =
d1 > d2 Cele două resorturi au aceeași secțiune, dar lungimi diferite. Resortul mai scurt are constanta elastică mai mare decât cel mai lung (k1 > k2).
Energia potențială elastică crește cu creșterea constantei elastice.
- Măsoară distanța parcursă de bilă când comprimi mai puțin resortul, respectiv când îl comprimi la maxim.
Resortul comprimat la maxim deplasează mai mult bila.
Energia potențială elastică crește cu creșterea comprimării resortului.
Concluzia experimentului:
Energia potențială elastică este direct proporțională cu constanta elastică și cu deformarea corpului elastic.
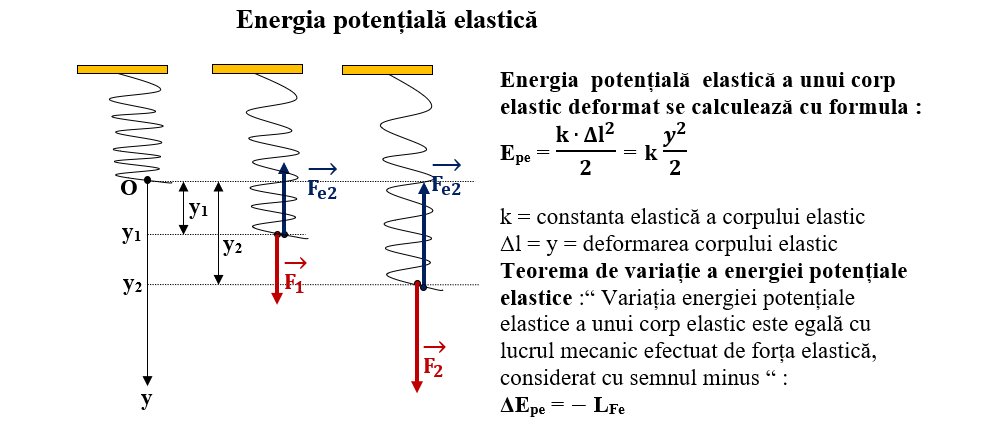
Energia potențială elastică (Epe) este energia pe care o are un corp deformat elastic, adică alungit sau comprimat.
Starea de referință căreia i se atribuie energia potențială elastică nulă, este starea nedeformată a corpului elastic.
Energia potențială elastică a unui corp elastic deformat se calculează cu formula:

unde:
k = constanta elastică a corpului elastic
Δl = y = deformarea corpului elastic
Lucrul mecanic, L, efectuat de forța elastică :
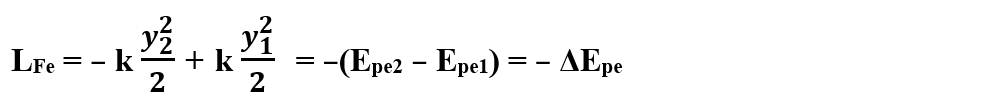
Această relație ne arată că lucrul mecanic efectuat de forța elastică este un lucru mecanic rezistent și nu depinde de drum, ci numai de pozițiile (alungirile) inițială și finală ale resortului. Deci, forța elastică este o forță conservativă.
🔓 Problemă rezolvată
1. Cât este energia potențială elastică a unui resort cu 150 N/m comprimat cu 30 cm?
Rezolvare:
Scriem datele problemei și transformăm în SI:
k = 150 N/m
Δl = 30 cm = 30/100 m = 0,3 m
Epe = ?
Scriem formula energiei potențiale elastice și înlocuim datele problemei:
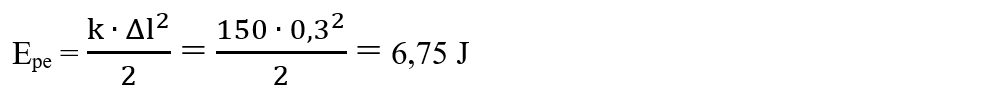
2. Un corp este intercalat între două resorturi nedeformate cu constantele elastice k1 = 30 N/m, respectiv k2 = 50 N/m, care sunt fixate pe orizontală între două suporturi. Se deplasează corpul spre stânga cu Δx2 = 10 cm, sub acțiunea unei forțe F. Cât este energia potențială acumulată într-un resort echivalent cu sistemul celor două resorturi la comprimarea (destinderea) cu Δx ?
Rezolvare:
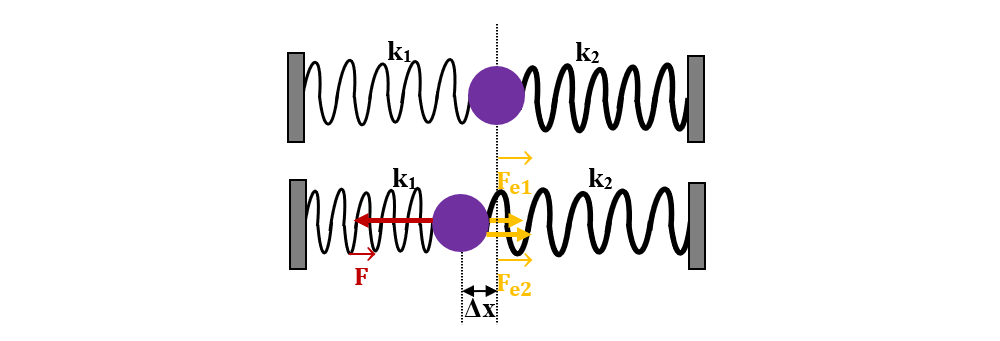
Forței deformatoare (F) i se opun două forțe elastice Fe1 și Fe2, care au valorile:
Fe1 = k1 ∙ Δx1
Fe2 = k2 ∙ Δx2
Suma celor două forțe este forța elastică totală apărută în acest sistem, egală în modul cu forța deformatoare, dar de sens opus:
Fe = Fe1 + Fe2
Comprimarea unui resort (Δx1) este egală cu alungirea celuilalt resort (Δx2), deci:
Δx = Δx1 = Δx2
Înlocuim cele două forțe elastice în ecuația:
Fe = Fe1 + Fe2 = k1 ∙ Δx + k2 ∙ Δx = (k1 + k2) ∙ Δx
Se observă că cele două resorturi sunt legate în paralel, având constanta elastică echivalentă:
k = k1 + k2
Energia potențială acumulată de un resort echivalent cu cele două legate în paralel este: