IV.3. Randamentul planului înclinat.
Randamentul unui dispozitiv reprezintă raportul dintre lucrul mecanic util (Lutil) efectuat de dispozitiv și lucrul mecanic consumat (Lconsumat) pentru funcționarea acestuia, sau raportul dintre puterea utilă (Putilă) și puterea consumată (Pconsumată).
Randamentul se notează cu litera grecească eta, η și se obține prin formula:

🔦 Observație
a) Randamentul nu are unitate de măsură, deoarece reprezintă raportul dintre două mărimi fizice identice. Spunem că randamentul este o mărime fizică adimensională.
b) Valoarea randamentului este pozitivă și subunitară, adică mai mică decât 1.
c) Randamentul se exprimă sub formă de procente ( % ).
Randamentul planului înclinat este egal cu raportul dintre lucrul mecanic efectuat pentru ridicarea uniformă a unui corp pe verticală (Lutil) și lucrul mecanic utilizat pentru urcarea uniformă a corpului pe planul înclinat (Lconsumat).
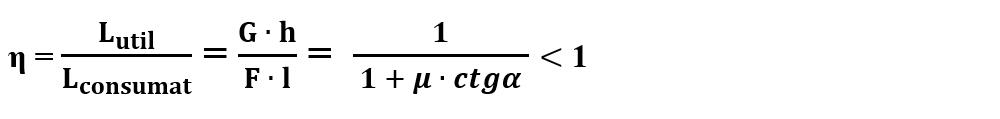

Corpul urcă uniform pe planul înclinat atunci când :
| F | = | Gt + Ff |
Gt = G ∙ h/l = G ∙ sin α
| Ff | = μ ∙ | N | = μ ∙ | Gn | = μG ∙ cosα
| F | = | Gt + Ff | = | G ∙ sinα + μ ∙ G ∙ cosα | = m ∙ g ∙ (sinα + μ ∙ cosα)
Lc = Gt + Ff = m ∙ g ∙ l (sinα + μ ∙ cosα)
Lu = G ∙ h = m ∙ g ∙ h

Deoarece sinα = h/l, rezultă:

Dacă simplificăm prin sinα, obținem formula randamentului unui plan înclinat:

Randamentul unui dispozitiv se mai poate exprima și prin raportul dintre puterea utilă (Pu) și puterea consumată (Pc):

Dacă notăm puterea pierdută cu Pp și scriem bilanțul puterilor:
Pc = Pu + Pp
Înlocuind în formula randamentului obținem :

🔓 Problemă rezolvată
1. Calculează randamentul planului înclinat.
Iată tabelul cu datele experimentale:

Rezolvare:
Transformăm toate dimensiunile în metri:
h1 = 2 cm = 0,02 m
h2 = 6 cm = 0,06 m
h3 = 11 cm = 0,11 m
l = 23 cm = 0,23 m
Calculăm pentru fiecare determinare randamentul:

Observăm faptul că odată cu creșterea înălțimii planului înclinat (implicit și a unghiului α al planului), randamentul planului înclinat crește.