IV.1.4. Lucrul mecanic al forței elastice.

Considerăm un resort care la momentul t₀ este nedeformat.

La momentul t₁ alungirea resortului este Δl₁ = y₁, produsă de o forță deformatoare F₁.

La momentul t₂ alungirea resortului este Δl₂ = y₂, produsă de o forță deformatoare F₂.

În timp ce resortul se alungește iau naștere și forțe elastice egale în modul cu forțele deformatoare, dar de sens opus, adică

Deoarece forța elastică este variabilă, lucrul mecanic, L, efectuat de ea între pozițiile 1 și 2, trebuie calculat utilizând forța elastică medie, F_em:
L = -F_em ∙ (y₂ – y₁)

Întrucât modulul forței elastice variază direct proporțional cu alungirea, forța medie este media aritmetică a valorilor forțelor elastice F_e1 și F_e2:

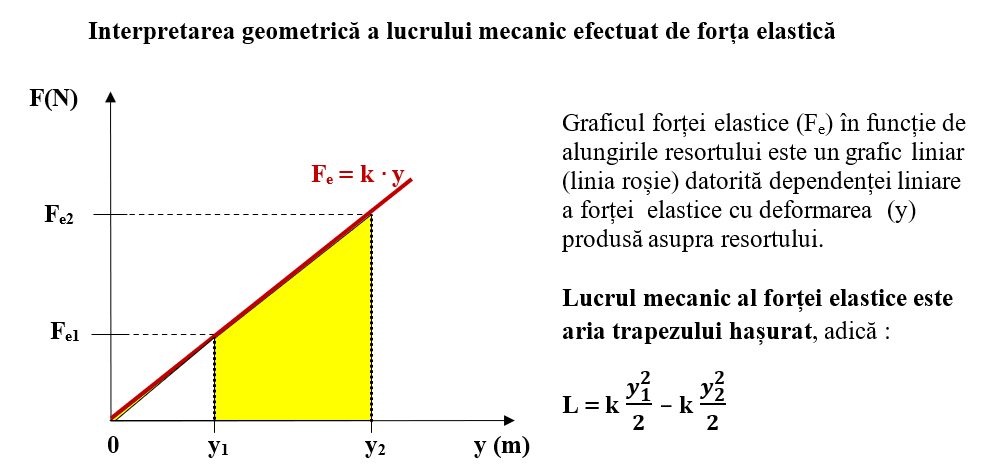
Lucrul mecanic, L, efectuat de forța elastică este:

Dar, F_e1 = k ∙ y₁ și F_e2 = k ∙ y₂, obținem expresia lucrului mecanic, L, efectuat de forța elastică:

Această relație ne arată că lucrul mecanic efectuat de forța elastică este un lucru mecanic rezistent și nu depinde de drum, ci numai de pozițiile (alungirile) inițială și finală ale resortului. Deci, forța elastică este o forță conservativă.

Lucrul mecanic efectuat de forța deformatoare (F) este un lucru mecanic motor, cu următoarea expresie:

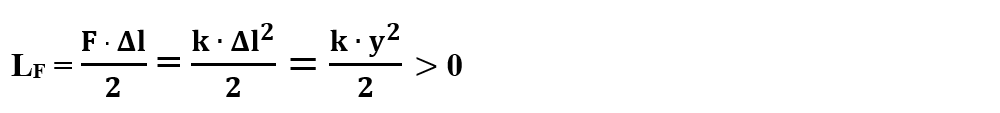
unde
k = constanta elastică a resortului
Δl = y = deformarea resortului

Lucrul mecanic efectuat de forța elastică (o forță conservativă) nu depinde de drumul efectuat de punctul material supus acțiunii acelei forțe, ci numai de pozițiile extreme ale resortului. El este egal cu lucrul mecanic efectuat de forța deformatoare, dar cu semnul minus, deoarece forța elastică se opune deformării resortului.

Lucrul mecanic efectuat de forța elastică este un lucru rezistent, cu următoarea expresie:

unde
k = constanta elastică a resortului
Δl = y = deformarea resortului