III.7.4. Sateliți artificiali.Viteze cosmice.
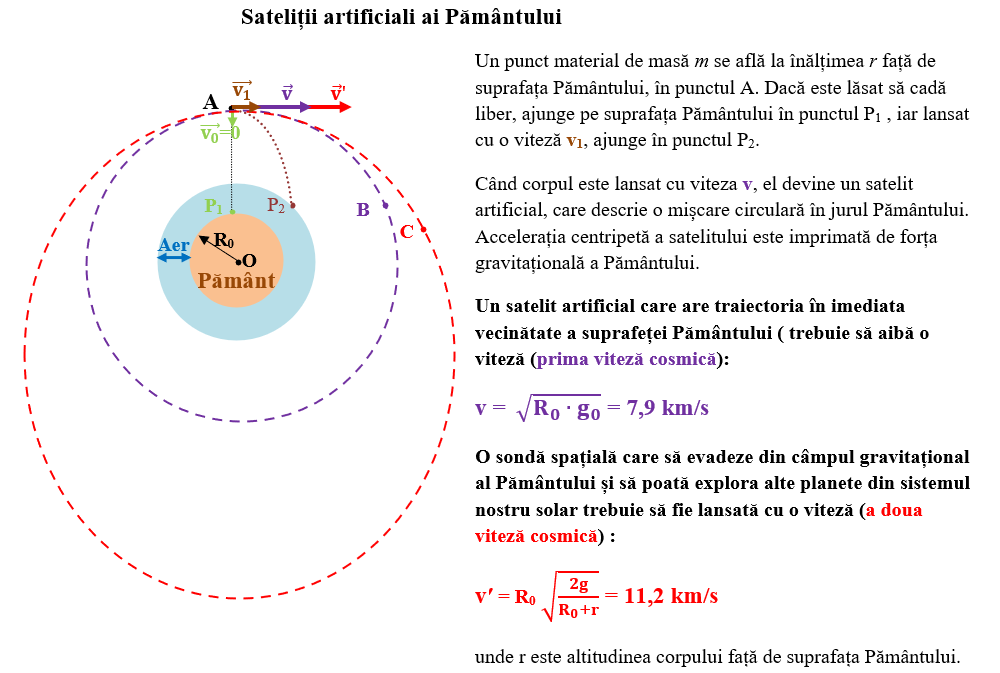
Din legea atracției universale putem determina viteza minimă care trebuie imprimată unei nave cosmice sau unui satelit artificial pentru a se plasa pe o orbită circulară în jurul planetei sau chiar de a părăsi sistemul nostru solar.
🔦 Observație
Pentru ca o rachetă să evadeze din câmpul gravitațional al Soarelui pentru a explora alte sisteme solare din galaxia noastră trebuie să fie lansată cu o viteză, numită a treia viteză cosmică, de 42 km/s.
Viteza necesară părăsirii galaxiei noastre, numită a patra viteză cosmică, este de 290 km/s.
Tipuri de sateliți:
- Sateliți artificiali cu orbită joasă (LEO – Low Earth Orbit)
Aceștia orbitează deasupra Pământului la distanțe cuprinse între 150 și 2000 Km. O rotație completă este efectuată în 90 minute, iar timpul în care un punct aflat pe Pământ are vizibilitate directă cu satelitul este de 15 minute. Întârzierea și atenuarea semnalelor transmise, sunt reduse. Timpul de viață se limitează de la câteva luni, la maxim un an. În prezent, se află 470 sateliți cu orbita joasă.
- Sateliți artificiali cu orbită medie (MEO – Medium Earth Orbit)
Orbitează pe orbite eliptice dispuse deasupra polilor sau deasupra Ecuatorului la distanțe cuprinse între 10.000 și 20.000 Km. Timpul în care un punct aflat pe Pământ are vizibilitate directă cu satelitul este 120 ... 360 de minute. Întârzierea și atenuarea semnalelor transmise prin acest tip de sateliti, sunt destul de mari. Sunt utilizați în special în rețele GPS și pentru comunicații de voce și date. La momentul actual pe orbita Pământului se află 69 sateliți cu orbita medie.
- Sateliți artificiali cu orbită geostationară (GEO – Geostationary Earth Orbit) Sateliții geostaționari sunt plasați pe orbite situate deasupra Ecuatorului la distanța fixă de 35.786 Km. Se rotesc cu aceeași viteză și în același sens cu Pământul. Un satelit geostaționar poate acoperi în orice moment 42,2% din suprafața planetei. Timpul în care un punct aflat pe Pământ are vizibilitate directă cu satelitul este de 24 de ore. Întârzierea și atenuarea semnalelor transmise, sunt foarte mari, iar costurile de plasare a acestor sateliți pe orbită sunt de asemenea foarte mari. Sunt utilizați în general pentru comunicații de orice tip, supravegherea militară sau meteorologică. Pe orbita Pământului se afla 423 sateliți cu orbita geostaționară.
🔓 Probleme rezolvate
1. Calculează perioada de rotație (revoluție) a unui satelit artificial care are traiectoria în imediata vecinătate a suprafeței Pământului și care a fost lansat cu prima viteză cosmică v = 7,9 km/s.
Rezolvare:
Considerăm că înălțimea (r) de la care a fost lansat satelitul este foarte mică comparativ cu raza Pământului (R0) și vom considera raza orbitei circulare egală chiar cu R0, adică R0 + r ≅ R0.
Perioada mișcării circulare uniforme este intervalul de timp în care mobilul realizează o rotație completă, parcurgând circumferința cercului, de lungime 2πR. În acest interval de timp spațiul unghiular descris de poziția inițială și cea finală este de 2π radiani (360°). Prin urmare, viteza unghiulară este:

Scriem relația care face legătura între viteza tangențială v și viteza unghiulară ω:

Înlocuim datele numerice pentru a calcula perioada de revoluție a satelitului, considerând raza Pământului de 6400 km:

Satelitul artificial încheie o rotație completă în jurul Pământului la fiecare 85 min.
2. Știind că sateliții geostaționari sunt folosiți în telecomunicații (transmit emisiunile radio-TV) și că au o perioadă de revoluție egală cu cea de rotație a Pământului în jurul propriei axe, T ≅ 24 h, calculează înălțimea r la care trebuie plasat pentru a rămâne într-un punct fix față de Pământ.
Rezolvare:
Considerăm înălțimea (r) a satelitului geostaționar față de suprafața Pământului. Deci distanța totală a satelitului față de centrul Pământului (centrul atracției gravitaționale) este egală cu suma dintre raza Pământului (R0) și înălțimea r, adică raza orbitei circulare este egală cu R0 + r.
Scriem relația care face legătura între viteza tangențială v și viteza unghiulară ω:

Greutatea satelitului este egală cu forța centripetă:
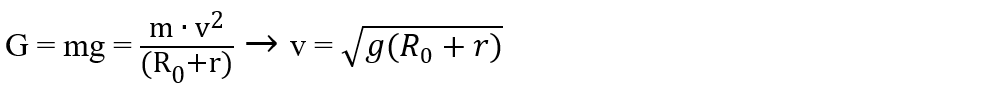
Ținând cont de variația accelerației gravitaționale cu altitudinea, obținem pentru viteza satelitului:

Înlocuim viteza în formula perioadei și apoi ridicăm la pătrat pentru a scăpa de radical:
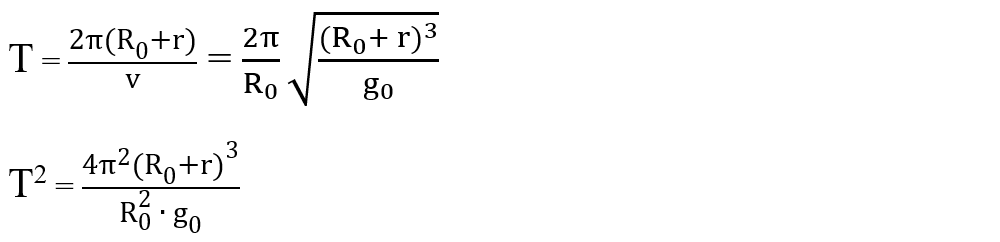
Înlocuim datele numerice considerând R0 ≅ 6400 km, T ≅ 24 h și g ≅ 10 m/s2 și obținem:
r ≅ 35800 km