III.6.4. Determinarea coeficientului de frecare cu ajutorul planului înclinat.
👀 Experiment: Determinarea coeficientului de frecare la alunecare
Materiale necesare:
Plan înclinat cu unghi α reglabil (tribometru), corp paralelipipedic.
Teoria lucrării:
Pentru de determinarea coeficienților de frecare cinetic (μc) și static (μs) se utilizează un tribometru, care este un plan înclinat cu unghi α reglabil.
Planul înclinat este reprezentat printr-un triunghi dreptunghic care este asemenea cu triunghiul dreptunghic format de greutate și componentele sale. Din asemănarea triunghiurilor precizate se găsesc relațiile:

unde:
G = greutatea corpului care se descompune după cele două direcții perpendiculare Ox și Oy în Gt (greutatea tangențială) și Gn(greutatea normală)
F = forța de tracțiune
Ff = forța de frecare
N = reacțiunea normală
Corpul lăsat liber pe planul înclinat coboară uniform atunci când:
| Ff | = | Gt | și
| N | = | Gn |
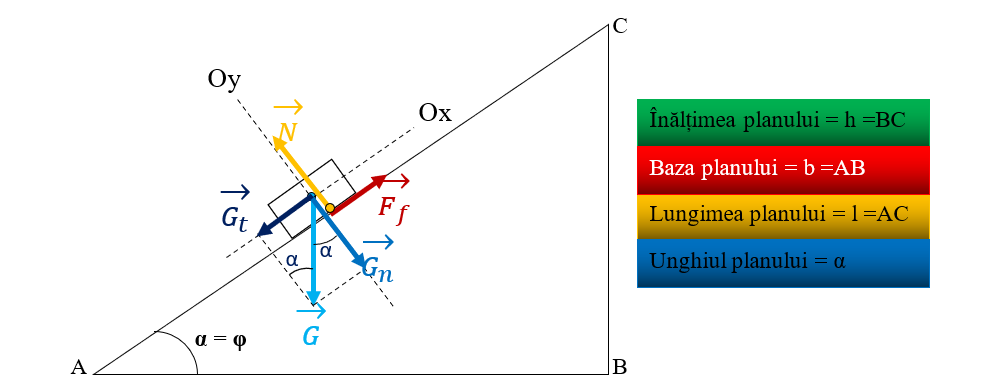
Pentru determinarea coeficientului de frecare la alunecare (cinetic), prin tatonări, se găsește un unghi α = φ, pentru care corpul coboară pe plan cu viteză constantă.
Ff = Gt = G ∙ sinφ
Din legea frecării avem relația:
Ff = μ ∙ N = μc ∙ G ∙ cosφ
Egalăm cele două ecuații ale Ff și scoatem necunoscuta μc:

μc = tg φ
Unghiul φ al planului înclinat pentru care corpul coboară uniform se numește unghi de frecare.
Modul de lucru:
- Se așază corpul paralelipipedic pe planul înclinat cu un unghi foarte mic.
- Se mărește treptat înclinarea planului, ciocănindu-l ușor cu mâna, până când corpul începe să coboare uniform pe plan. Se fixează planul la aceast unghi, numit unghi de frecare, φ.
- Se măsoară cu rigla înălțimea h și baza b a planului înclinat.
- Se măsoară cu raportorul unghiul de frecare φ.
- Se repetă operațiile de cel puțin trei ori și datele se trec în următorul tabel:

- Se compară rezultatele măsurătorilor:

Pentru determinarea coeficientului de frecare static se procedează în mod analog, numai că alunecarea corpului pe planul înclinat va fi accelerată și nu uniformă.
🔓 Probleme rezolvate
1. Un corp de 20 kg este deplasat pe orizontală sub acțiunea unei forțe de 100 N, care face un unghi de 45° cu orizontala. Știind coeficientul de frecare de 0,2, să se calculeze forța de frecare. Ce fel de mișcare are corpul? Se dă cos 45° = sin 45° = √2/2
Rezolvare:
Notăm datele problemei:
m = 20 kg
F = 100 N
α = 45°
μ = 0,2
Ff = ?
Desenăm forțele ce acționează asupra corpului:
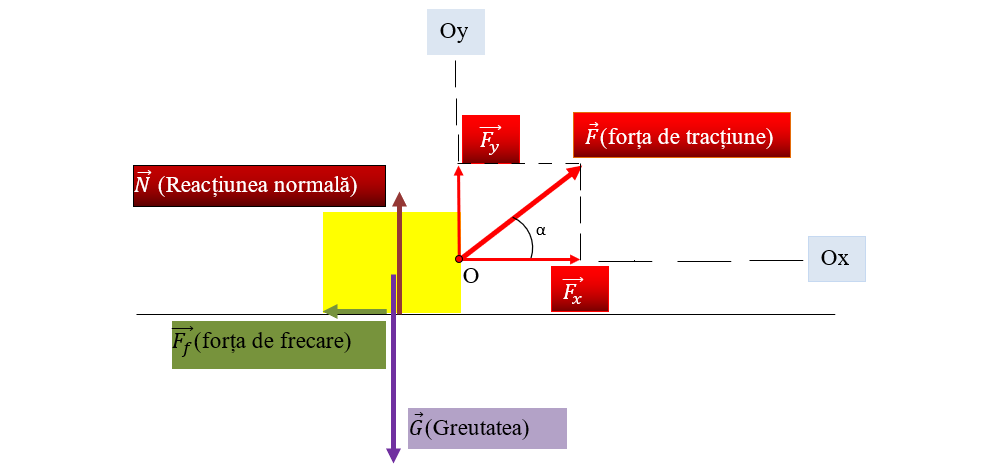
Calculăm componentele forței de tracțiune:
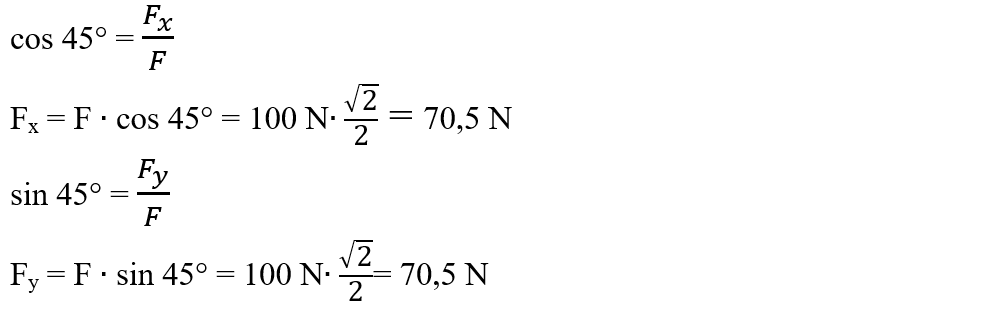
Calculăm greutatea corpului:
G = m ∙ g = 20 kg ∙ 10 N/kg = 200 N
Pe direcția verticală (Oy):
| G | = | Fy + N | => Ry = Fy + N – G = 0
(deoarece corpul se mișcă pe orizontală, forța rezultantă pe verticală trebuie să fie 0)
| G | = | Fy + N |
N = G – Fy = 200 N – 70,5 N = 129,5 N
Calculăm forța de frecare:
Modulul reacțiunii normale este egal cu modulul apăsării normale, fiind forțe pereche de tip acțiune-reacțiune.
Ff = μ ∙ N = 0,2 ∙ 129,5 N = 25,9 N
Pe direcția orizontală (Ox):
Rx = Fx - Ff = 70,5 N – 25,9 N = 44,6 N
Deoarece Fx > Ff, corpul se mișcă accelerat.
2. Un tren de 588 t pornește din stație sub acțiunea unei forțe de 117.600 N. Știind valoarea coeficientului de frecare de 0,005, determină viteza trenului după 60 s.
Rezolvare:
Notăm datele problemei:
m = 588 t = 588000 kg
F = 117600 N
μ = 0,005
Δt = 60 s
v = ?
Calculăm greutatea și forța de frecare:
G = m ∙ g = 588000 kg ∙ 10 N/kg = 5880000 N
Ff = μ ∙ N = μ ∙ G = 0,005 ∙ 5880000 N = 29400 N
Calculăm rezultanta celor două forțe ce acționează pe orizontală:
R = F - Ff = 117600 N – 29400 N = 88200 N
Deoarece F > Ff, corpul se mișcă accelerat.
Aplicăm ecuația Principiului mecanicii clasice: dacă asupra unui corp acționează o forță (forța rezultantă, R), atunci corpul se va mișca cu o accelerație cu aceeași direcție și sens cu forța rezultantă:
