Probleme rezolvate

🔓 Probleme rezolvate - Refracția luminii. Indicele de refracție

3.1. Să se calculeze indicele de refracție al apei, știind că viteza de propagare a luminii prin apă este 220000000 m/s. Voi trebuie să știți pe dinafară numai viteza luminii în vid.

• Scriem datele problemei:

  • c = 300000000 m/s
  • v = 220000000 m/s

• Scriem formula indicelui de refracție:

3.2. Să se calculeze viteza luminii prin diamant care are indicele de refracție de 2,42.

• Scriem datele problemei:

  • c = 300000000 m/s
  • n = 2,42

• Scriem formula indicelui de refracție:

• Scoatem necunoscuta din ecuație, astfel n coboară la numitor și v urcă la numărător în partea opusă (fiind extremi pot schimba locul între ei).

🔓 Probleme rezolvate recapitulative – Legile refracției

3.3. O rază de lumină provenită din aer mediu cu n = 1 cade sub un unghi de incidență de 45° pe suprafața altui mediu. Știind unghiul de refracție de 30°, se cere:

a) Cât este unghiul de reflexie?

b) Care este valoarea indicelui de refracție al celui de-al doilea mediu ?

c) Desenul fenomenului de reflexie și de refracție suferite de acestă rază.

d) Calculează viteza luminii prin al doilea mediu.

Rezolvare:

Scriem datele problemei:
n₁ = 1
n₂ = ?
i = 45°
r' = 30°
r = ? °
v₂ = ?

a) Unghiul de reflexie este egal cu unghiul de incidență de 45°.

b) Pentru a calcula indicele de refracție aplicăm legea a II-a a refracției:

c) Scriem formula indicelui de refracție și scoatem necunoscuta, v₁:

🔓 Probleme rezolvate recapitulative – Reflexia totală. Lentile. Formarea imaginii unui obiect în lentile. Formulele lentilelor. Ochiul uman. Defecte de vedere

3.4. Un scafandru aflat la o adâncime de 2m îndreaptă lanterna telefonului acvatic spre suprafața apei. Știind indicele de refracție al apei de 4/3 și cel al aerului de 1, află suprafața circulară a luminii care iese din apă. Cum variază această suprafață a luminii ieșită în aer cu creșterea adâncimii scafandrului?

Rezolvare:

• Scriem datele problemei:

  • h = 2 m

  • n₁ = 4/3

  • n₂ = 1

  • S = ?

• Se desenează traseul razelor de lumină care ies din apă:

• Se aplică legea a II-a a refracției punând condiția ca unghiul de incidență să fie egal cu unghiul limită (i = l) și unghiul de refracție r = 90°. Știind că sin 90° = 1 obținem:

• Calculăm cos i cu formula:

• Calculăm tg i și raza suprafeței circulare:

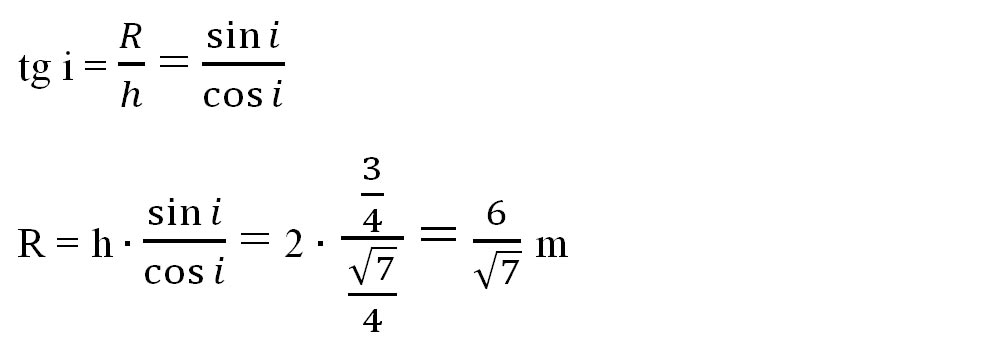
• Calculăm aria suprafeței circulare:

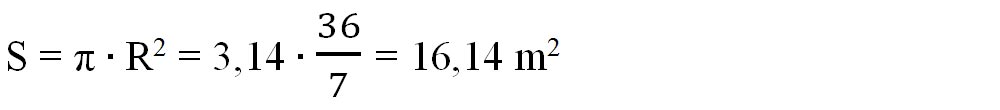
• Observăm că raza suprafeței luminoase din aer este direct proporțională cu adâncimea scafandrului, deci aria acestei suprafeței crește odată cu adâncimea scafandrului.

3.5. O prismă optică are unghiul refringent A = 90° și indicele de refracție √2. Află dacă o rază de lumină ce cade pe o față a prismei sub un unghi de 45° poate suferi reflexie totală pe una dintre fețele prismei.

Rezolvare:

• Secțiunea transversală a prismei este un triunghi dreptunghic isoscel cu A = 90° și B = C = 45°.

• În ΔDI₁I₂: D = r' + i₂

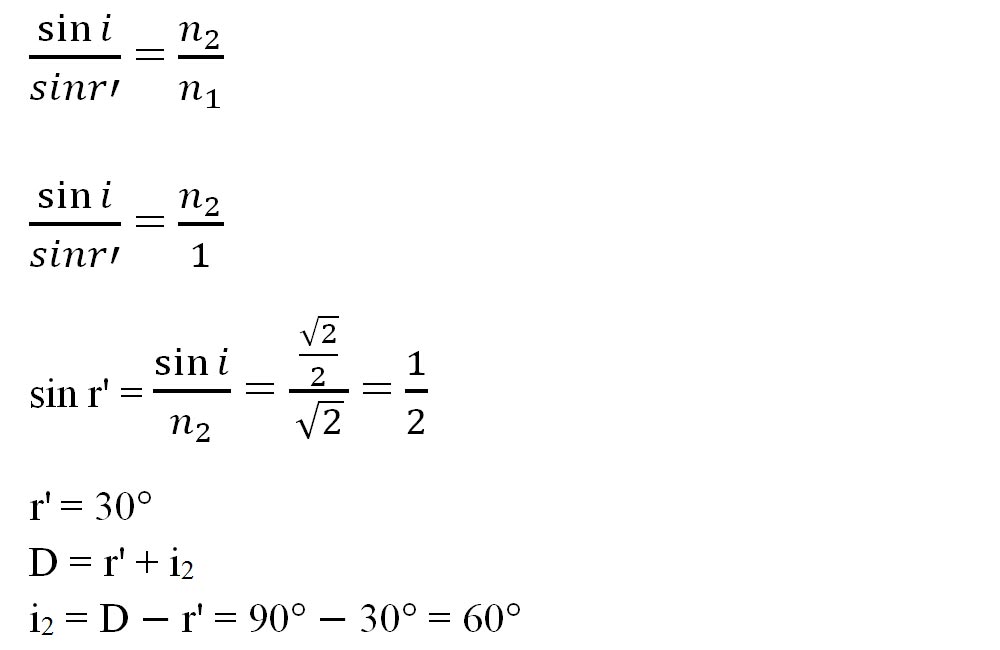
• Pentru a afla unghiul limita aplicăm a II–a lege a refracției punând condiția ca unghiul de incidență să fie egal cu unghiul limită (i₂ = l) și unghiul de refracție r' = 90°. Știind că sin 90° = 1 obținem:

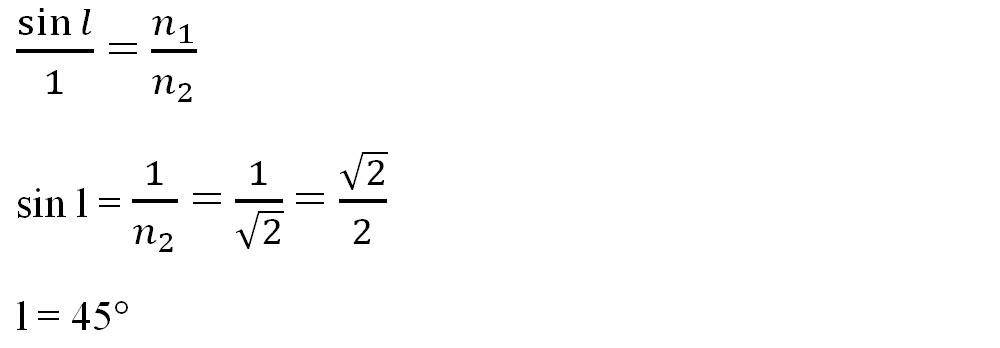
• Cum i₂ > l și primul mediu (sticla prismei) are indicele de refracție mai mare decât al doilea mediu (aerul) înseamnă că sunt îndeplinite ambele condiții pentru a se produce reflexie totală.

3.6. În fața unei lentile convergente cu distanța focală de 20 cm se așază o lumânare la o distanță de 60 cm.

Se cere:

a) Desenează formarea imaginii lumânării în această lentilă.

b) Calculează coordonata (distanța) la care trebuie așezat un ecran pe care să se formeze imaginea clară a lumânării.

c) De câte ori este mărită/micșorată imaginea? Caracterizează imaginea lumânării.

d) Câte dioptrii are această lentilă?

Rezolvare:

• Notăm datele problemei:

  • f = 20 cm (distanța focală a lentilei se ia pozitivă, întrucât lentila este convergentă și refractă lumina prin focarul pozitiv)

  • x₁ = - 60 cm (distanța de la obiectul AB la lentilă se ia negativă, întrucât este pe axa numerelor întregi negativă)

  • x₂ = distanța de la imaginea A'B' la lentilă = ?

  • β = ?

  • C = ?

a)

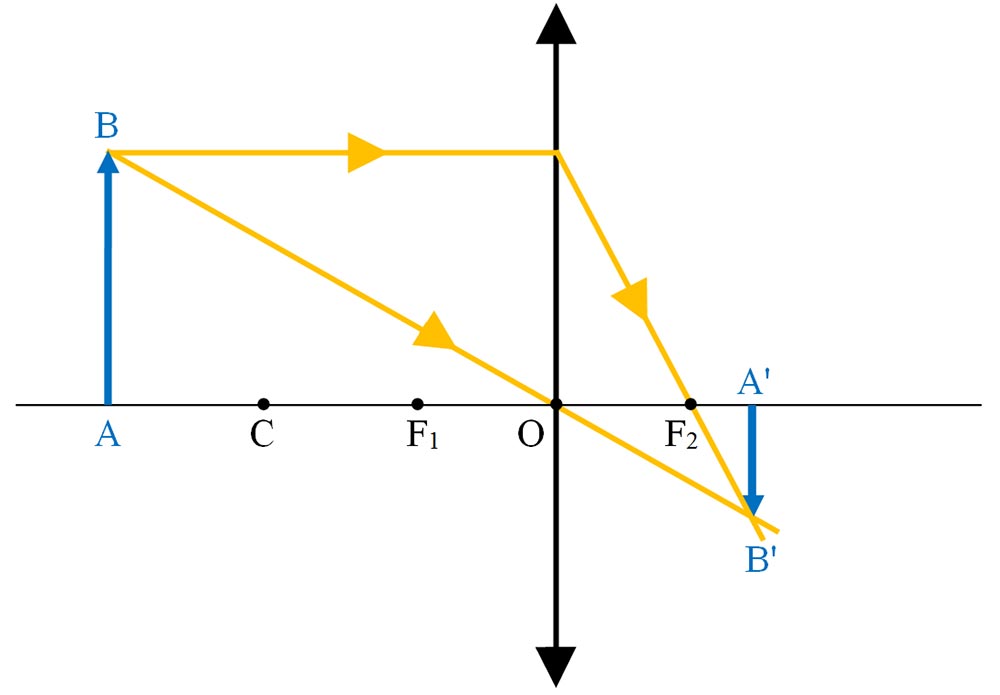
b) Scriem formula fundamentală a lentilelor subțiri:

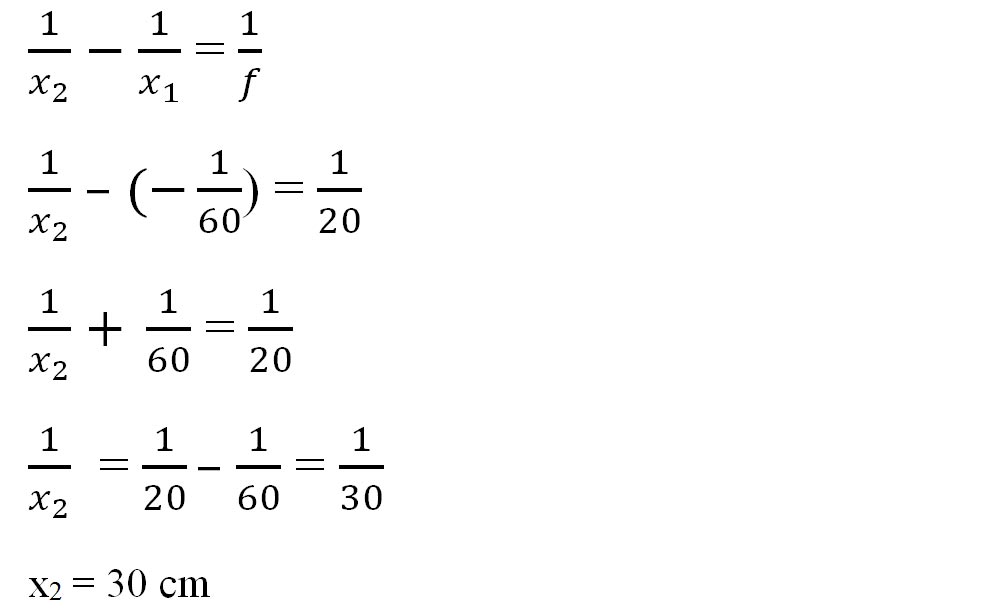
c)

d) Calculăm convergența lentilei:

3.7. Știind că microscopul este compus din două lentile convergente, obiectivul are o distanță focală foarte mică și este așezat în apropierea obiectului și că ocularul preia imaginea formată de obiectiv și o mărește și mai mult decât obiectivul, imaginea finală fiind virtuală, desenează formarea imaginii unui obiect într-un microscop.

Rezolvare:

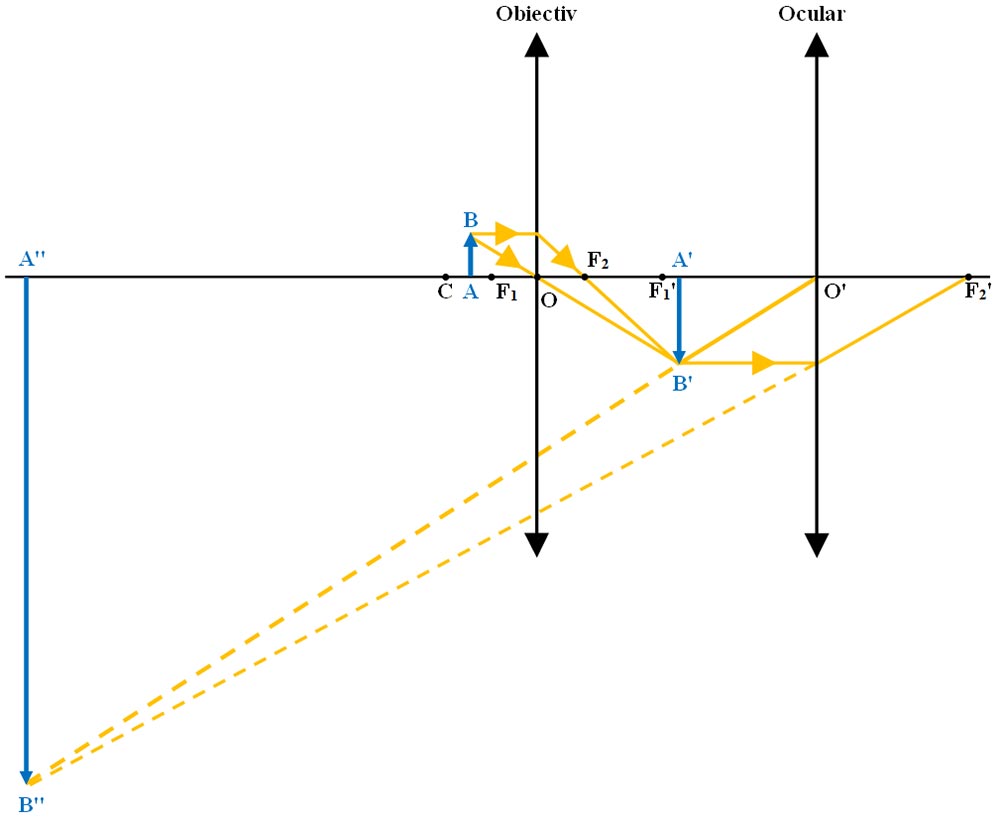
3.8. Determinarea indicelui de refracție al unui mediu folosind rigla.

O rază de lumină (folosește un laser) intră într-un vas gol (cu aer) și apoi vasul se umple cu apă cu indice de refracție necunoscut. Află indicele de refracție al apei.

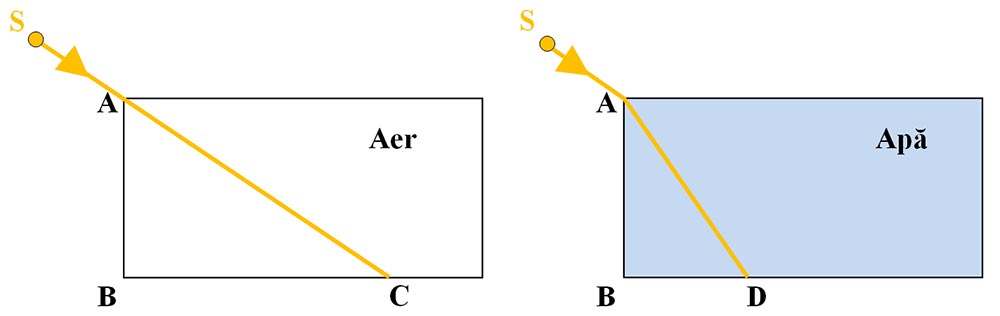
Rezolvare:

• Se măsoară segmentele AB (înălțimea apei din vas), BC și BD cu ajutorul riglei (ruletei).

• Se calculează cu ajutorul teoremei lui Pitagora AC și AD.

• Se calculează sin i și sin r:

• Aplicăm legea a doua a refracției, știind că n_aer = 1.

• Scoatem necunoscuta n_apă:

Exemplu aplicativ :

AB = 4 cm

BC = 5 cm

BD = 2,5 cm

AC² = AB² + BC² = 4² + 5² = 16 +25 = 41

AC = √41 = 7,21 cm

AD² = AB² + BD² = 4² + 2,5² = 16 + 6,25 = 22,25

AD = √22,25 = 4,71 cm

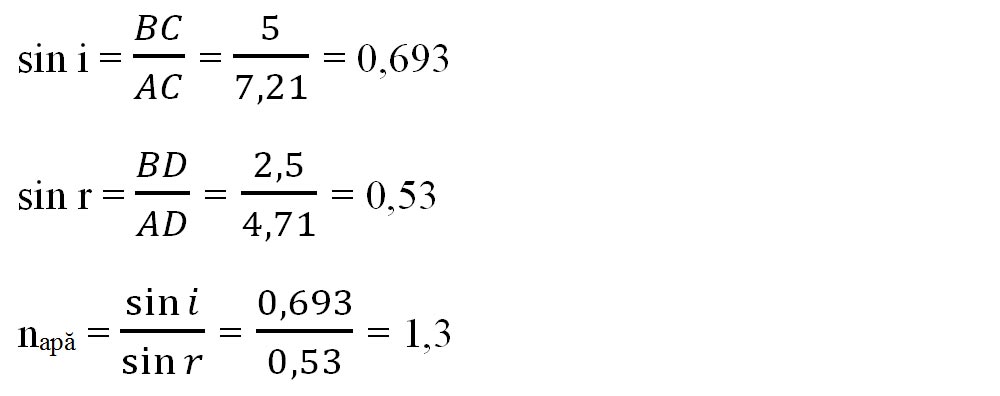
3.9. Scrie un cuvânt cu creionul roșu. Apoi cu un creion albastru taie cuvântul scris până nu se mai vede ce ai scris. Uită-te la ce ai scris cu un filtru albastru (corp transparent albastru). Ce observi ?

Privind prin geamul albastru vei vedea ce ai scris cu roșu. Care este explicația?

Geamul albastru este opac pentru lumina roșie, dar este transparent pentru lumina albastră, deoarece filtrul albastru transmite numai radiația albastră iar pe celelalte culori le absoarbe.

Filtrul albastru elimină propria culoare și de aceea noi nu vedem ștersătura cu culoarea albastră și vedem numai culoarea roșie reflectată de coala albă colorată cu roșu.

3.10. De ce un om nu vede clar obiectele când înoată sub apă ? Care om, cu miopie sau cu hipermetropie, vede mai clar sub apă ?

Chiar dacă apa este limpede noi nu vedem clar în apă, deoarece apa are indicele de refracție aproximativ egal cu cel al umoarei apoase și sticloase astfel încât refracția luminii în ochi se produce puțin diferit ca în aer. În apă imaginea obiectelor nu se mai formează pe retină (ca în aer), ci în spatele ei și de aceea obiectele se văd cețoase (ca la hipermetropi).

Miopii văd mai clar sub apă decât oamenii normali sau cei cu hipermetropie, deoarece imaginea obiectelor la ei în aer se formează în fața retinei, iar sub apă se va deplasa mai spre retină.

Ochelarii de scafandru au lentile plan-concave (convergente), goale în interior, pentru ca lumina să intre în aerul din interiorul căștii și vederea să aibă loc ca în aer.