Probleme rezolvate

🔓 Problemă rezolvată - Electrizarea și sarcina electrică. Interacțiunea dintre corpurile electrizate. Metode de electrizare

2.1. Ce valoare are sarcina învelișului electronic a unui atom de oxigen știind că acesta are Z = 8? Se dă e = sarcină electrică elementară = 1,6 ∙ 10^-19 C.

Rezolvare:

Știind că Z = nr. p⁺ din nucleu = nr. ē din învelișul electronic, înseamnă că atomul de oxigen are în înveliș 8 electroni. Deci n = 8.

Sarcina unui corp (q) este un multiplu întreg al sarcinii electrice elementare :

Q = n ∙ e, unde n = nr. ē și e = sarcină electrică elementară = 1,6 ∙ 10^-19 C.

Q = n ∙ e = 8 ∙ 1,6 ∙ 10^-19 C = 12,8 ∙ 10^-19 C.

🔓 Probleme rezolvate - Legea lui Coulomb

2.2. Două corpuri punctiforme încărcate cu sarcinile q₁ = 2 nC, respectiv q₂ = 5 nC, se află la distanța de 40 cm în aer. Calculează forțele de interacțiune electrică.

Rezolvare:

• Notăm datele problemei și transformăm în SI :

  • q₁ = 2 nC = 2 ∙ 10^(-9) C

  • q₂ = 5 nC = 5 ∙ 10^(-9) C

  • r = 40 cm = 0,4 m

  • F = ?

• Desenăm forțele electrice, egale în modul dar de sens opus :

• Scriem Legea lui Coulomb:

2.3 Două corpuri punctiforme, încărcate cu sarcinile q1 = -4 pC, respectiv q2 = 6 pC, se află la distanța de 300 mm în aer. Calculează și reprezintă forțele de interacțiune electrică.

Rezolvare:

• Notăm datele problemei și transformăm în SI:

q₁ = -4 pC = -4 ∙ 10 ^-12 C

q₂ = 6 pC = 6 ∙ 10^-12 C

r = 300 mm = 0,3 m

F = ?

• Desenăm forțele electrice de atracție, egale în modul, dar de sens opus:

• Scriem Legea lui Coulomb:

🔓 Problemă rezolvată - Intensitatea curentului electric

2.4. La capetele unei porțiuni de circuit există o tensiune de 24 V.

a) Calculează lucrul mecanic efectuat de sursa electrică pe acea porțiune de circuit prin care trece o sarcină de 8C.

b) Știind că intensitatea curentului electric este de 2 A, află timpul în care se efectuează acest lucru mecanic ?

Rezolvare :

• Notăm datele problemei :

  • U = 24 V

  • q = 8 C

  • I = 2 A

  • L = ?

  • t = ?

• a) Scriem formula de definiție a tensiunii electrice :

• b) Scriem formula de definiție a intensității curentului

🔓 Problemă rezolvată - Rezistența electrică

2.5. Printr-un conductor trece un curent electric de 0,3 A, având la capete o tensiune de 24 V. Află rezistența conductorului.

Rezolvare :

• Scriem datele problemei:

  • U = 24 V

  • I = 0,3 A

  • R = ?

• Scriem formula rezistenței electrice :

🔓 Problemă rezolvată - Legea lui Ohm pentru întregul circuit

2.6. Pe un bec de lanternă este scris 0,2 A și 6,3 V. Se leagă becul la o baterie de 9 V (becul este în condiții normale de funcționare). Determină:

a) Rezistența electrică a filamentului becului.

b) Sarcina electrică ce trece prin filamentul becului timp de o oră.

c) Tensiunea internă a bateriei.

d) Rezistența internă a bateriei.

e) Intensitatea curentului de scurtcircuit.

Rezolvare:

• Notăm datele problemei:

  • I = 0,2 A

  • U = 6,3 V

  • E = 9 V

  • t = 1h = 3600 s

• Calculăm necunoscutele :

🔓 Probleme recapitulative - Electrizare. Circuit electric simplu

2.7. Dacă la bornele unui generator electric se leagă un rezistor cu o rezistență de 20 Ω, prin circuit se măsoară cu ampermetru un curent de 3 A. Știind rezistența generatorului de 1 Ω, află tensiunea electromotoare notată pe acest generator. Ce intensitate are curentul electric la scurtcircuitarea rezistorului?

Rezolvare:

• Scriem datele problemei:

  • R = 20 Ω

  • I = 3 A

  • r = 1 Ω

  • E = ?

• Aflăm tensiunea la bornele rezistorului din legea lui Ohm pentru o porțiune de circuit:

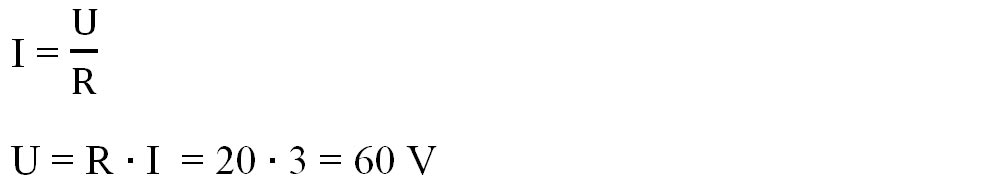
• Aflăm tensiunea internă din legea lui Ohm pentru o porțiune de circuit :

• Calculăm tensiunea electromotoare aplicând relația dintre cele trei tensiuni ale unui circuit (Tensiunea la bornele circuitului exterior este egală cu tensiunea la bornele rezistorului, fiind un singur consumator, adică U_b = U):

  • E = U_b + u = 60 + 3 = 63 V

• Aplicăm legea lui Ohm pentru întreg circuitul, punând condiția ca rezistența circuitului exterior (a rezistorului) să fie 0 :

2.8. Un fir de cupru este legat la o baterie. Firul metalic are rezistivitatea 1,68 ∙ 10^-8Ω ∙ m. El este străbătut de un curent de 120 mA, când are o lungime de 4 m și o secțiune transversală de 0,2 mm². Să se determine tensiunea la capetele firului.

Rezolvare:

• Notăm datele problemei și le transformăm în SI:

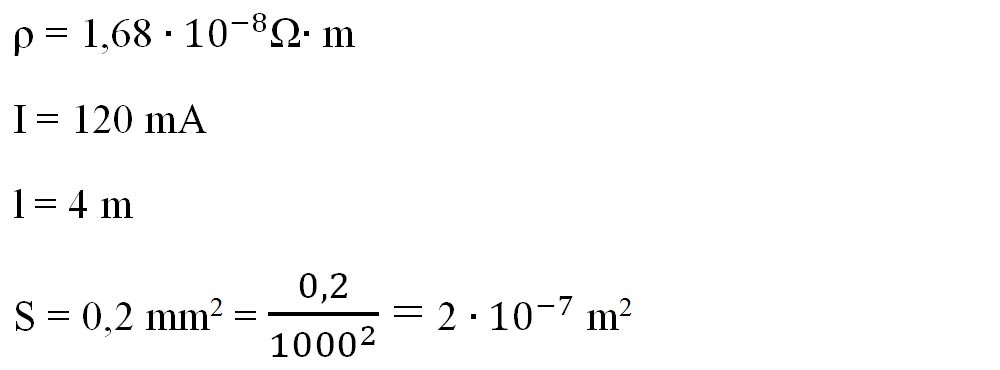
• Calculăm rezistența firului de cupru, aplicând formula rezistenței în funcție de dimensiunile conductorului:

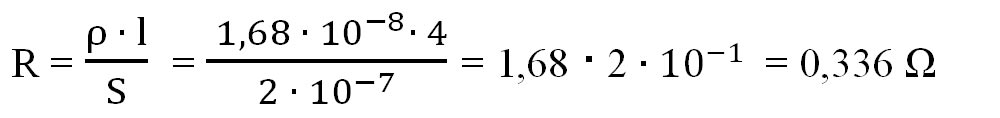
• Calculăm tensiunea la capetele conductorului, din legea lui Ohm pentru o porțiune de circuit :

2.9. La o baterie electrică ce are tensiunea electromotoare de 4,5 V se alimentează un bec. Știind tensiunea la bornele becului de 4 V și rezistența becului de 20 Ω, determină:

a) Intensitatea curentului ce trece prin bec.

b) Numărul de electroni ce traversează secțiunea transversală a filamentului becului în 20 min.

c) Tensiunea internă a bateriei.

d) Rezistența internă a bateriei.

e) Puterea electrică a becului.

f) Energia electrică consumată de bec în 20 min, atât în SI, cât și în kWh.

g) Intensitatea curentului la scurtcircuit.

Rezolvare:

• Notăm datele problemei:

  • E = 4,5 V

  • U_b = 4 V

  • R = 20 Ω

  • t = 20 min = 20 ∙ 60 s = 1200 s

  • I = ?

a) Scriem legea lui Ohm pentru o porțiune de circuit (bornele becului) :

b) Numărul de electroni (n) ce traversează secțiunea transversală a filamentului becului în 20 min.

• n = ?

• t = 20 min = 20 ∙ 60 s = 1200 s

• Scriem formula de definiție a intensității curentului electric :

• Scoatem necunoscuta n :

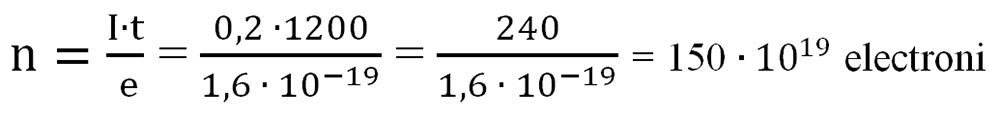
c) Tensiunea internă: u = ?

• Scriem relația dintre cele trei tensiuni ale unui circuit:

  • E = U_b + u

  • u = E – U_b = 4,5 – 4 = 0,5 V

d) Rezistența internă: r = ?

• Scriem formula rezistenței:

e) Puterea electrică a becului: P = ?

• P = U ∙ I = 4 ∙ 0,2 = 0,8 W

f) Energia electrică W =? J, kWh.

g) Intensitatea curentului la scurtcircuit I_sc = ?

2.10. Un acumulator de 110 V alimentează un bec prin filamentul căruia trece o sarcină de 20 C timp de 10 s. Știind tensiunea internă de 10 V, determină:

a) Tensiunea la bornele becului, U_b = ?

b) Intensitatea curentului electric, I = ?

c) Rezistența becului, R = ?

Rezolvare:

• Notăm datele problemei:

  • E = 110 V

  • Q = 20 C

  • t = 10 s

  • u = 10 V

a) Scriem relația dintre cele trei tensiuni electrice:

• E = U_b + u

• U_b = E – u = 110 – 10 = 100 V

b) Scriem formula de definiție a intensității curentului electric :

c) Scriem legea lui Ohm pentru o porțiune de circuit (bornele becului):

2.11. La bornele unei surse electrice se leagă pe rând câte un rezistor cu rezistența R₁, respectiv R₂. Când rezistorului cu rezistență R₁, îi aplicăm la capete o tensiune U₁ = 5 V, prin el trece un curent de 3 A. Când unui alt rezistor cu rezistența R₂ îi aplicăm la capete o tensiune U₂ = 8 V, prin el trece un curent de 2 A. Cât este tensiunea electromotoare a sursei electrice și rezistența sa internă ?

Rezolvare:

• Notăm datele problemei:

  • U₁ = 5 V

  • I₁ = 3 A

  • U₂ = 8 V

  • I₁ = 2 A

  • E = ?

  • r = ?

• Calculăm rezistențele celor două rezistoare:

• Aplicăm legea lui Ohm pentru întreg circuitul, atât pentru I₁, cât și pentru I₂:

2.12. Fie o grupare serie de n₁ = 6 rezistoare identice, cu valoarea R₁ = 2 Ω care are rezistența echivalentă egală cu a unei grupări paralel de n₂ rezistoare identice, cu rezistența R₂ = 48 Ω fiecare. Determină numărul de rezistoare, n₂, grupate în paralel.

Rezolvare:

• Notăm datele problemei:

  • n₁ = 6 rezistoare

  • R₁ = 2Ω

  • R₂ = 48Ω

  • n₂ = ?

• Calculăm rezistența echivalentă serie:

• Calculăm rezistența echivalentă paralel:

• Egalăm R_s cu R_p și scoatem necunoscuta n₂:

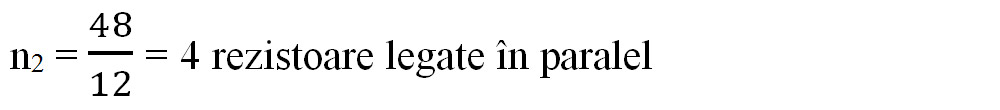
2.13. Un consumator alimentat la o tensiune de 220 V, în 8h de funcționare consumă o energie electrică de 10 kWh.

a) Ce valoare are intensitatea curentului electric prin acest consumator?

b) Ce putere electrică are el?

Rezolvare:

• Notăm datele problemei și le transformăm în SI:

  • U = 220 V

  • t = 8 h = 8 ∙ 3600 s = 28.800 s

  • W = 10 kWh = 10 ∙ 1000 W ∙ 3600 s = 36 ∙ 10⁶ J

a) Scriem formula energiei electrice și scoatem necunoscuta I:

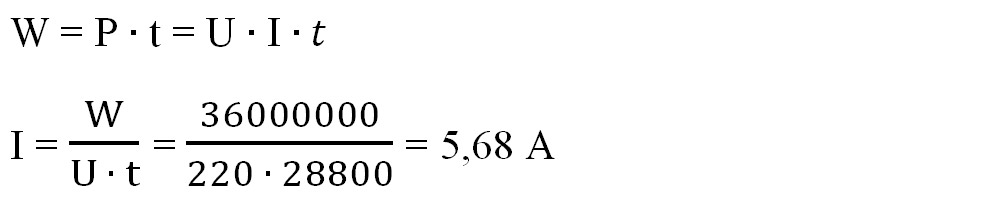
b) Calculăm puterea consumatorului:

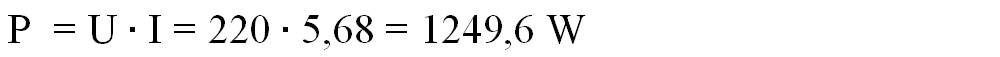
2.14. Neglijând pierderile de energie, calculați ce lucru mecanic efectuează motorul unui troleibuz, timp de 8h, dacă curentul este de 120 A și tensiunea de 500 V. Exprimați rezultatul și în kWh.

Rezolvare:

• Notăm datele problemei și le transformăm în SI:

  • U = 500 V

  • I = 120 A

  • t = 8 h = 8 ∙ 3600 s = 28.800 s

  • L = ? J, kWh

• Scriem formula intensității curentului electric și scoatem necunoscuta Q:

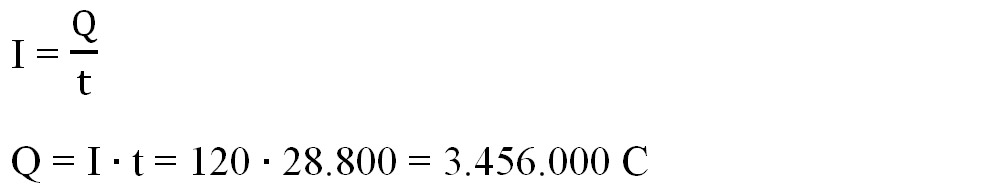
• Scriem formula tensiunii electrice și scoatem necunoscuta L:

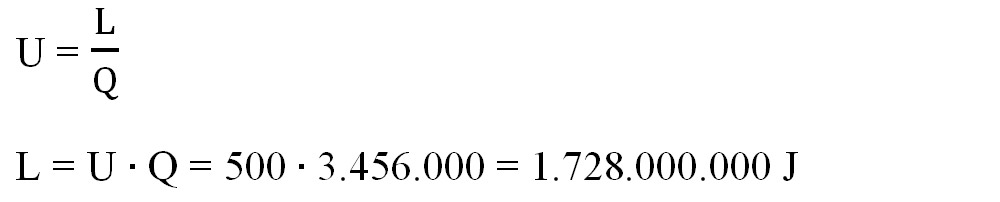
• Transformăm lucrul mecanic din J în kWh, știind că 1J = 1W ∙ 1s :

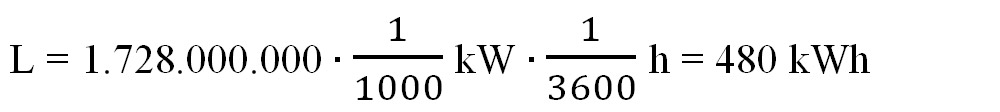
2.15. Cât costă pe lună (30 de zile) consumul unui bec de 100 W, care luminează 6 h pe zi, știind că 1 kWh costă 50 de bani?

Rezolvare:

• Notăm datele problemei:

  • W = ? kWh

  • Cost = ?

  • P = 100 W = 100/1000 = 1/10 kW

  • 1 kWh costă 50 bani

  • t = 30 ∙ 6 h = 180 h

• Calculăm energia electrică în kWh:

2.16. Ce căldură degajă un bec de 25 W în timp de 1h, știind că din energia electrică consumată 4% se transformă în energie luminoasă ?

Rezolvare:

• Notăm datele problemei:

  • Q = ?

  • P = 25 W

  • t = 1 h = 3600 s

  • W → Lumină 4%

• Calculăm energia electrică:

• Calculăm căldura degajată de bec:

🔓 Problemă rezolvată - Gruparea rezistoarelor

2.17. Determină rezistenţa echivalentă a rezistoarelor din următoarea grupare mixtă :

Rezolvare:

• Se notează pe rețea toate nodurile cu litere mari.

• Mergem pe conturul circuitului de la un nod la altul și echivalăm grupările de rezistoare cu rezistoarele echivalente, serie sau paralel.

• Între nodul A și B avem 2 rezistoare pe aceeași latură, deci sunt în serie și le echivalăm cu R_s1.

• Între nodul B și C avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p1.

• Între nodul A și E avem 1 rezistor pe care îl copiem.

• Între nodul E și F avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p2.

• Calculăm rezistențele echivalente :

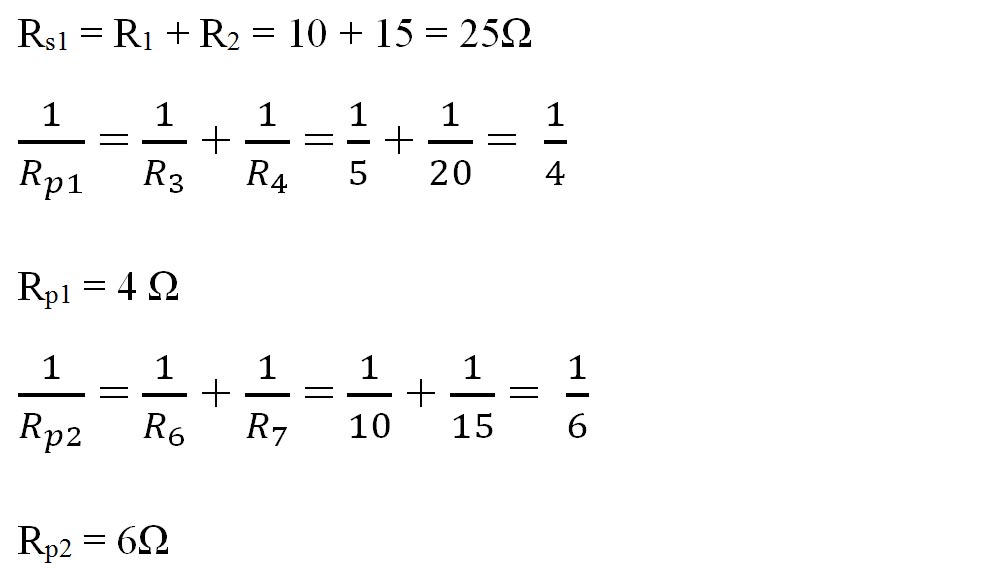
• Pe schema nouă, continuăm să echivalăm grupările de rezistoare :

  • Între nodul A și D, pe latura de sus, avem 2 rezistoare pe aceeași latură (R_s1 cu R_p1), deci sunt în serie și le echivalăm cu R_s2 .

  • Între nodul A și D, pe latura din mijloc, avem 2 rezistoare pe aceeași latură (R₅ cu R_p2), deci sunt în serie și le echivalăm cu R_s3 .

• Calculăm rezistențele echivalente:

  • R_s2 = R_s1 + R_p1 = 25 + 4 = 29Ω

  • R_s3 = R₅ + R_p2 = 2 + 6 = 8Ω

• Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

  • Între nodul A și D avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p3.

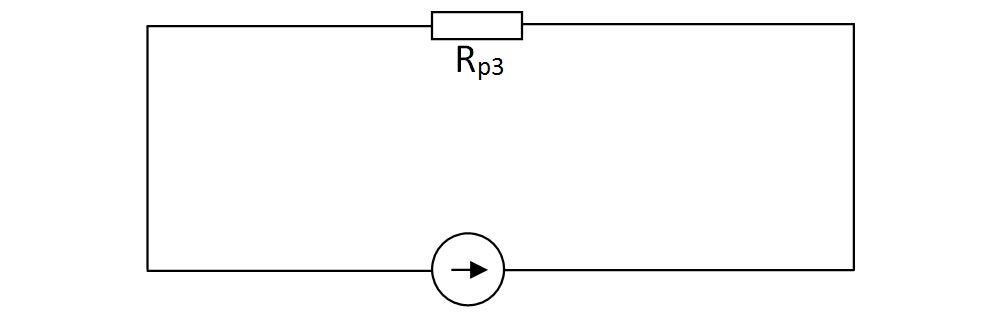
• Calculăm rezistența echivalentă:

🔓 Problemă rezolvată - Extindere: Teoremele lui Kirchhoff

2.18. Determină intensitățile curenților din următorul circuit ramificat:

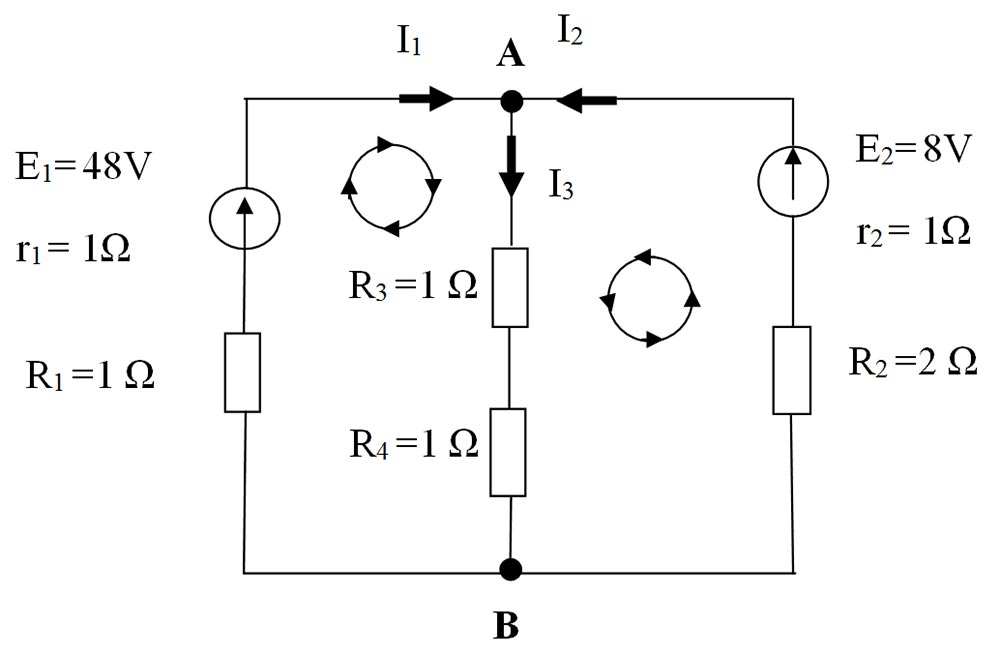
Rezolvare:

• Notăm cu litere mari nodurile rețelei (A și B).

• Notăm laturile rețelei, stabilim arbitrar sensurile curenților de pe fiecare latură:

  • AE₁B (I₁)

  • AE₂B (I₂)

  • AR₃B (I₃)

• Notăm ochiurile simple ale rețelei. Stabilim arbitrar (cum dorim) câte un sens de parcurs pentru fiecare ochi (orar sau antiorar).

• Aplicăm prima teoremă a lui Kirchhoff: “Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul respectiv“.

• Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea, deci pentru un singur nod:

  • I₁ + I₂ = I₃

• Aplicăm a doua teoremă a lui Kirchhoff: “Suma algebrică a tensiunilor electromotoare pentru un ochi de circuit este egală cu suma algebrică a căderilor de tensiune din acel ochi de circuit“, pentru două ochiuri simple:

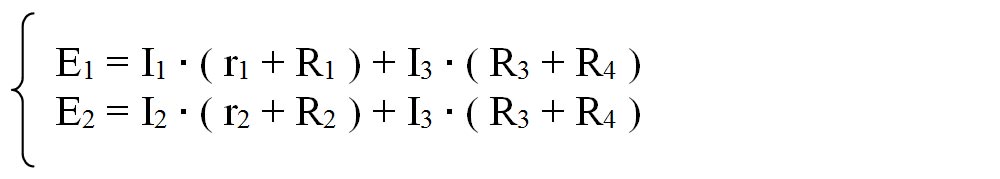
• Facem un sistem de 3 ecuații și cu cele trei necunoscute I₁, I₂, I₃

• Înlocuim datele numerice:

• Scoatem pe I₁ din prima ecuație: I₁ = I₃ – I₂ și îl înlocuim în a doua ecuație

• Se înlocuiește I₂ într-o ecuație cu I₃:

• Din prima ecuație îl aflăm pe I₁:

🔓 Probleme rezolvate recapitulative - Rețele electrice. Efectul curentului electric. Forța electromagnetică

2.19. Determină rezistenţa echivalentă a rezistoarelor din următoarea grupare mixtă:

Rezolvare:

• Notăm pe rețea toate nodurile cu litere mari.

• Mergem pe conturul circuitului de la un nod la altul și echivalăm grupările de rezistoare cu rezistoare echivalente, serie sau paralel.

• Între nodul A și B, în partea stângă, avem 2 rezistoare pe aceeași latură (R₁ și R₂), deci sunt în serie și le echivalăm cu R_s1.

• Între nodul A și B avem 2 rezistoare pe aceeași latură (R₄ și R₇), deci sunt în serie și le echivalăm cu R_s2.

• Între nodul B și C avem 1 rezistor (R₃), pe care îl copiem.

• Între nodul A și C avem 2 rezistoare pe aceeași latură (R₅ și R₆), deci sunt în serie și le echivalăm cu R_s3.

• Între nodul B și C avem sursa pe care o copiem.

• Calculăm rezistențele echivalente :

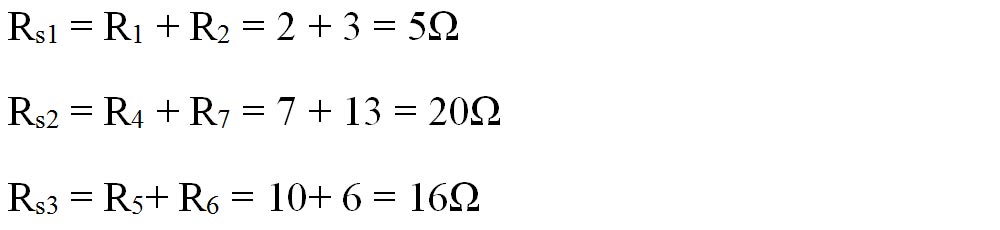
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

• Între nodul A și B avem 2 rezistoare (R_s1 și R_s2) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p1.

• Restul schemei o copiem.

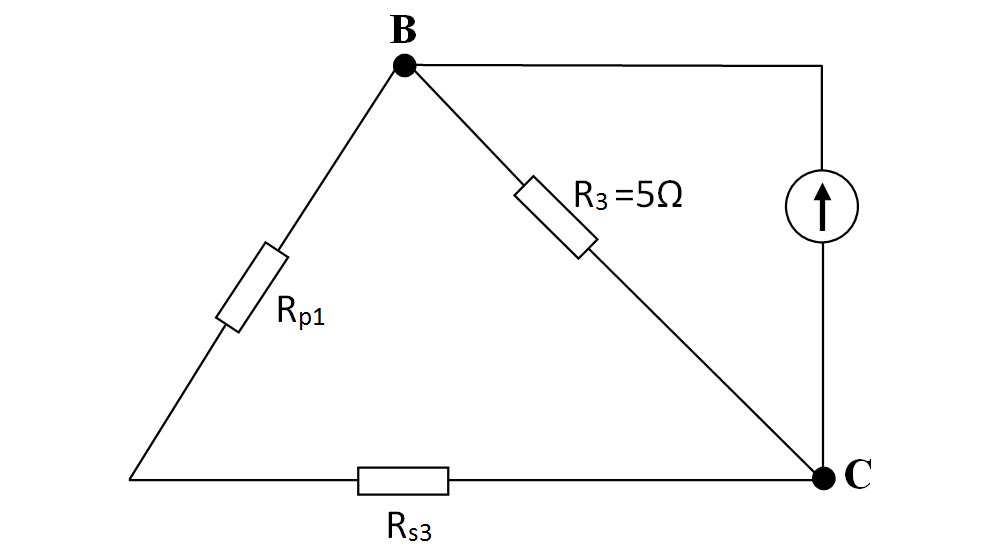
• Calculăm rezistența echivalentă:

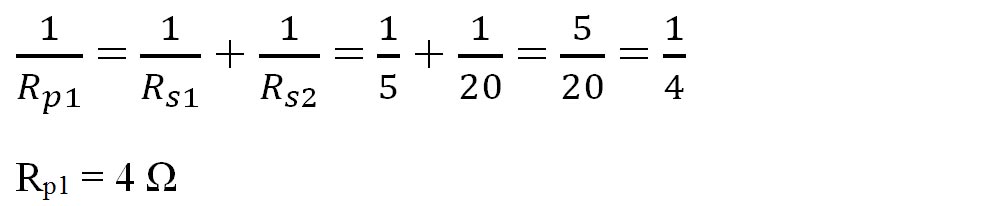
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

• Între nodul B și C avem 2 rezistoare (R_p1 și R_s3) pe aceeași latură, deci sunt în serie și le echivalăm cu R_s4.

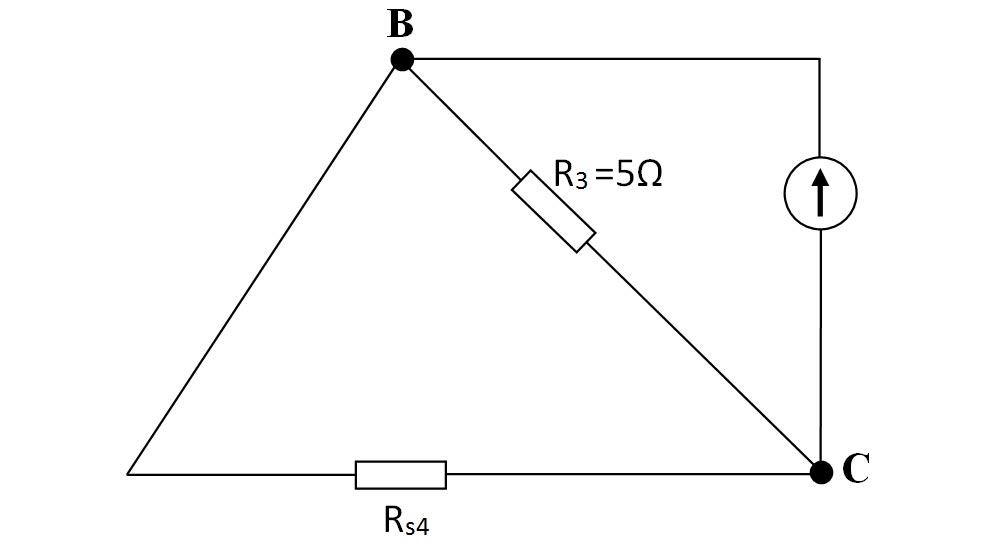
• Calculăm rezistența echivalentă:

Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

• Între nodul B și C avem 2 rezistoare (R_s4 și R₃) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p2.

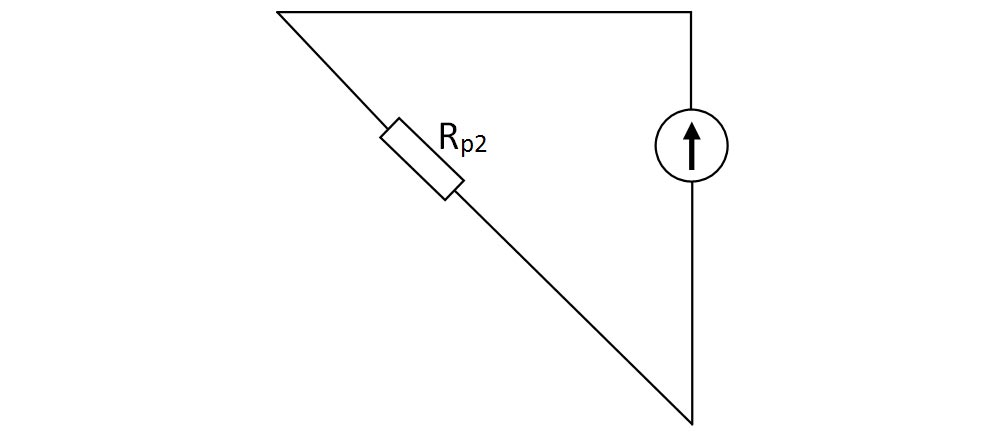
• Calculăm rezistența echivalentă a întregii grupări:

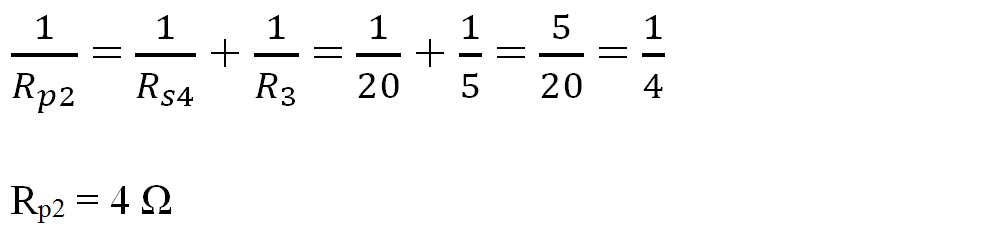
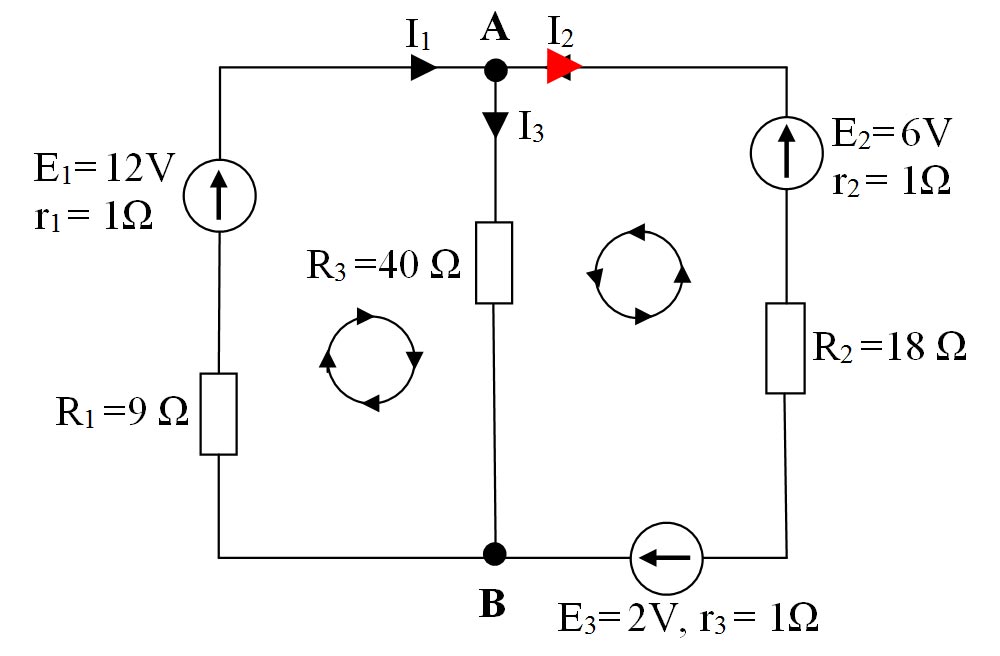
2.20. Determină intensitățile curenților din următorul circuit ramificat:

Rezolvare

• Notăm cu litere mari nodurile rețelei (A și B).

• Notăm laturile rețelei, stabilim arbitrar sensurile curenților de pe fiecare latură:

  • AE1B (I₁)

  • AE2B (I₂)

  • AR3B (I₃)

• Notăm ochiurile simple ale rețelei. Stabilim arbitrar (cum dorim) câte un sens de parcurs pentru fiecare ochi (orar sau antiorar).

• Aplicăm prima teoremă a lui Kirchhoff: “Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul respectiv“.

• Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea, în cazul nostru pentru un singur nod:

  • I₁ + I₂ = I₃

• Aplicăm a doua teoremă a lui Kirchhoff: “Suma algebrică a tensiunilor electromotoare pentru un ochi de circuit este egală cu suma algebrică a căderilor de tensiune din acel ochi de circuit“, pentru două ochiuri simple:

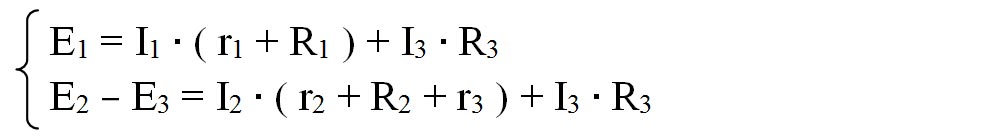
Facem un sistem de 3 ecuații și cu cele trei necunoscute I₁, I₂, I₃.

• Înlocuim datele numerice:

• Scoatem pe I₁ din prima ecuație:

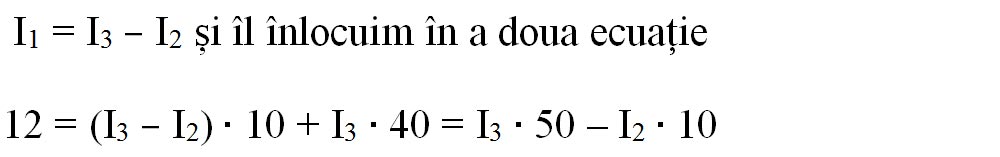
• Rezolvăm sistemul cu 2 ecuații și 2 necunoscute, prin reducere:

• Înlocuim pe I₃ într-o ecuație cu I₂:

• Schimbăm sensul curentului I₂ ales inițial, arbitrar, pe rețea:

• Din prima ecuație îl aflăm pe I₁:

2.21. Realizează electroliza fluorurii de zinc (ZnF₂).

2.22. Rezistența internă a unei baterii crește treptat în timp de când a fost fabricată, chiar dacă nu este folosită, tensiunea electromotoare a acesteia rămânând constantă. Astfel bateria, în timp, chiar dacă nu este folosită, va produce un curent de intensitate mai mică, crescându-i rezistența internă.

Poți determina vârsta unei baterii legând ampermetrul la bornele bateriei și citind intensitatea la scurtcircuit.

Pentru o baterie de 1,5 V, I_sc = 2-3 A, când este nou fabricată.

a) Determină cât este rezistența internă a bateriei când este nouă și la ce valoare ajunge când I_sc = 1,3 A.

b) Determină cât este rezistența internă a acumulatorului de 12V când este nou, știind că are o intensitate la scurtcircuit I_sc = 40A.

2.23. O sursă electrică de t.e.m. de 12 V are o rezistență internă de 0,5 Ω. Ea este legată la un bec cu rezistența de 10 Ω.

Se cere:

a) Cât este intensitatea curentului ce trece prin bec dacă rezistența ampermetrului este de 0,001 Ω (considerăm că nu este un ampermetru ideal care are rezistența zero)?

b) Cât este intensitatea măsurată de ampermetru dacă scoatem becul din circuit ?

c) Cât este intensitatea curentului dacă la bornele becului legăm un voltmetru care nu este ideal, având o rezistență de 100.000 Ω ( voltmetrul ideal are rezistența care tinde spre infinit, pentru a nu permite trecerea curentului prin acesta și astfel se obține citirea corectă) ?

d) Dacă legăm direct voltmetrul la bornele sursei, cât este intensitatea curentului ?

Rezolvare:

• Scriem datele problemei:

  • E = 12 V

  • r = 0,5 Ω

  • R_b = 10Ω

  • R_A = 0,001 Ω

  • R_V = 100.000 Ω

a)

• Becul și rezistorul ampermetrului și rezistența sursei sunt în serie și au rezistența echivalentă:

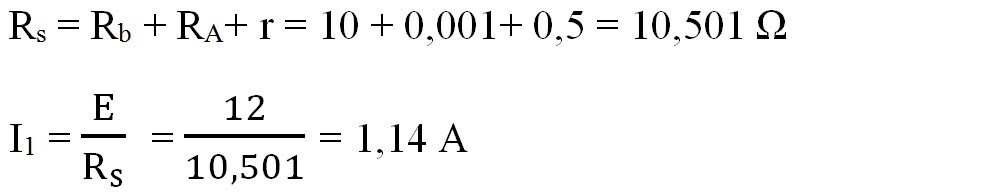
b)

• Dacă ampermetrul ar fi fost unul ideal, cu rezistența 0, el ar fi scurtcircuitat sursa și ar fi măsurat curentul de scurtcircuit cu formula

• Însă acest ampermetru nu are rezistența 0 și vom avea o intensitate:

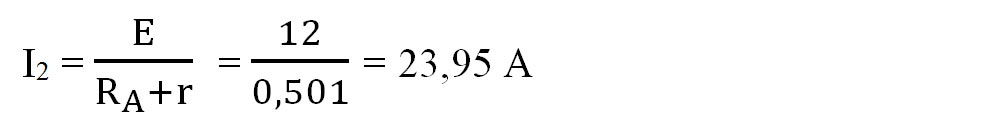
c)

• R_b și R_V sunt în paralel și le calculăm rezistența echivalentă R_p:

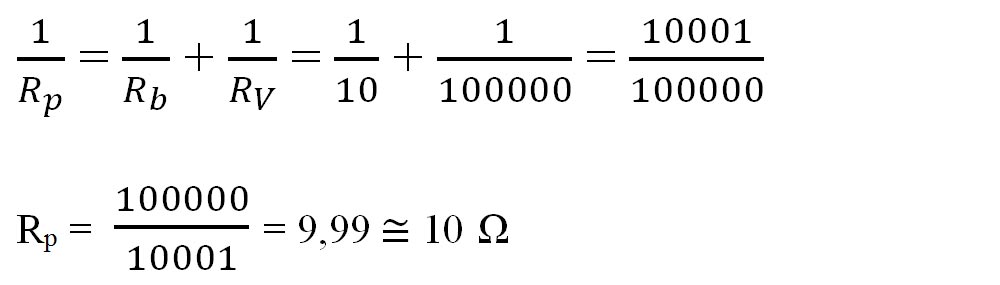
• R_p, R_A și r sunt în serie și au rezistența echivalentă:

d)

• Legând direct voltmetrul la sursă, r și R_V vor fi în serie și intensitatea va deveni:

Dacă voltmetru ar fi fost unul ideal (cu rezistența infinită), intensitatea curentului ar fi fost zero.

2.24. Un resort are lungimea inițială de 10 cm. Când suspendăm de el o tijă de fier cu mase marcate de 20 g, lungimea lui este de 14 cm. Sub tija de fier se așază un electromagnet legat la o baterie, caz în care lungimea resortului ajunge la 18 cm.

Se cere:

a) Greutatea tijei.

b) Forța de atracție a electromagnetului.

Rezolvare:

• Scriem datele problemei și le transformăm în SI:

  • l₀ = 10 cm = 0,1 m

  • l₁ = 14 cm = 0,14 m

  • l₂ = 18 cm = 0,18 m

  • m = 20 g = 0,02 kg

• a) Calculăm greutatea tijei cu masa marcată:

  • G = m ∙ g = 0,02 ∙ 10 = 0,2 N

  • Forța deformatoare este chiar greutatea tijei și ea produce o deformare de :

  • Δl₁ = l₁ – l₀ = 0,14 – 0,10 = 0,04 m

  • F = G = k ∙ Δl₁

• b) Calculăm a doua deformare:

  • Δl₂ = l₂ – l₀ = 0,18 – 0,10 = 0,08 m = 2 ∙ Δl₁

  • Forța de atracție a electromagnetului asupra tijei de fier adunată cu greutatea tijei produce a doua deformare a resortului:

  • F_a + G = k ∙ Δl₂

  • Fa = k ∙ Δl₂ - k ∙ Δl₁ = k ∙ 2Δl₁ - k ∙ Δl₁ = k ∙ Δl₁ = G = 0,2 N

2.25. Becurile B₂ și B₃ au valorile nominale de 6 V și 0,1 A și funcționează normal. Ampermetrul indică 300 mA. Este identic becul B₁ cu becurile B₂ și B₃ ?

Rezolvare:

I = I₁ + I₂ = 0,3 A

I₂ = I₃ + I₄ = 0,2 A

I₃ = I₄ = 0,1 A

I₁ = 0,1 A

Curentul din ramura principală cu sursa și cu ampermetrul se ramifică pe laturile becurilor B2 și B3, care fiind identice și legate în paralel, vor avea fiecare un curent de intensitate egală cu jumătate din curentul I₂, adică 0,1 A.

Becul B₁ are tensiunea nominală de 6 V și intensitatea nominală de I₁ = 0,1 A.

Deci becul B₁ este identic cu becurile B₂ și B₃.