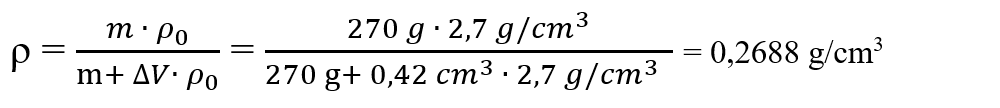IV.5. Probleme recapitulative rezolvate - Fenomene termice
1. Pentru a înțelege de ce șinele de cale ferată nu se sudează și când se montează se lasă un spațiu între ele, numit rost, să aflăm cu cât se dilată la 40 °C o șină de cale ferată, care la 0°C are lungimea de 10 m? Se dă coeficientul de dilatare termică liniară a fierului α = 0,000012 K-1.
Rezolvare:
Se scriu datele problemei:
t1 = 40 °C
t0 = 0 °C
l0 = 10 m
αFe = 0,000012 K-1
Scriem formula care definește coeficientul de dilatare liniară și care este constanta de proporționalitate dintre variația relativă a lungimii barei și variația temperaturii barei:

Dacă o bară de 10 m se dilată cu aproape jumătate de centimetru, atunci dacă ar fi sudată de o altă bară, în urma dilatării când este caniculă, s-ar deforma și trenul ar deraia de pe șine.
2. Două corpuri, 1 și 2, au fost puse în contact termic. Iată graficul evoluției în timp a temperaturii celor două corpuri:

Se cere:
a) Cât sunt temperaturile inițiale ale celor două corpuri?
b) Cât este temperatura de echilibru?
c) După câte minute cele două corpuri au ajuns la echilibru termic?
d) Ce fenomen suferă fiecare corp în timpul contactului termic?
Rezolvare:
a) Corpul 1 are temperatura inițială de 60 °C, fiind corpul cald și corpul 2 are temperatura inițială de 10 °C, fiind corpul rece (la momentul 0 min).
b) Temperatura de echilibru ale celor două corpuri (temperatura lor finală) este de 30 °C.
c) Cele două corpuri au ajuns la echilibru termic după 6 min.
d) În timpul contactului termic, corpul 1 (rece) primește căldură și se încălzește. Corpul 2 (cald) cedează căldură și se răcește.
3. În graficul de mai jos este reprezentată dependența volumului unui lichid de temperatură. Care este acest lichid?

Rezolvare:
La temperatura de 4 °C lichidul are cel mai mic volum și prin urmare, cea mai mare densitate.
Când lichidul este răcit sub 4 °C, volumul lui crește.
Când lichidul este încălzit peste 4 °C, volumul lui crește.
Aceste fenomene ciudate sunt suferite numai de apă și poartă numele de anomalia apei.
4. O lamă bimetalică este un ansamblu de două lame din metale diferite, prinse cu nituri. Ele la încălzire se curbează, deoarece ele își măresc lungimea diferit. Lamele bimetalice se utilizează drept întrerupătoare electrice la aparatele electrice cu termostat. În imaginile de mai jos sunt reprezentate doua lame bimetalice care s-au curbat la încălzire. Ordonează cele trei metale A, B și C în ordinea crescătoare a dilatării lor în lungime.

Rezolvare:
La prima lamă bimetalică, metalul A își mărește mai mult lungimea decât metalul B, prin încălzire.
La a doua lamă bimetalică, metalul B își mărește mai mult lungimea decât metalul C, prin încălzire.
Ordinea crescătoare a metalelor care se dilată liniar este C, B, A.
Exemplu:
Fe, Cu, Al
5. Unui corp prin încălzire îi scade densitatea cu 20%. Cu cât la sută îi crește volumul?
Rezolvare:
Notăm datele despre corp la temperatura camerei cu indice 1, iar cele după încălzire cu indice 2.
Scriem densitatea corpului după încălzire (ρ2) ținând cont că aceasta a scăzut cu 20% față de densitatea inițială (ρ1):

Scriem formula densit�ății ținând cont că prin încălzirea unui corp, la dilatare, se mărește doar volumul corpului, masa acestuia rămâne aceeași:

Se aduc toți termenii acestei ecuații la același numitor (10 ∙ V1 ∙ V2) și se renunță la numitor. De asemenea masa m se reduce la toți termenii:


Volumul corpului prin încălzire a crescut cu 25%.
6. De ce pe instrumentele de măsură cu scală gradată (vase gradate, rulete etc.) apare scris 20 °C?
Rezolvare:
Dilatarea instrumentelor de măsură cu scală gradată poate schimba distanța dintre diviziuni conducând la citiri eronate ale mărimilor măsurate. Ele sunt etalonate pentru a fi folosite la temperatura camerei de 20 °C.
7. Un corp de aluminiu de 270 g la temperatura de t0 = 20 °C are densitatea ρ0 = 2,7 g/cm3. Încălzind corpul la temperatura t = 80 °C, volumul său crește cu ΔV = 420 mm3. Ce densitate ρ are corpul la t = 80 °C?
Rezolvare:
Transformăm creșterea volumului în cm3 :

Scriem formula densității și scoatem volumul inițial al corpului:

Scriem volumul corpului după încălzire, mărit cu ΔV:
V = V0 + ΔV
Scriem formula densității după încălzirea, respectiv dilatarea corpului:

Înlocuim în formula obținută datele numerice și calculăm densitatea corpului la temperatura de 80 °C: