III.3. Difracția luminii (F1).

Când luminăm un corp opac, în spatele acestuia se formează o zonă întunecată (umbra corpului), deoarece lumina se propagă în linie dreaptă și nu poate ocoli obstacolul din calea ei.

Când obstacolul are dimensiuni foarte mici, apare fenomenul de difracție și frontul de undă se deformează, astfel încât lumina se propagă și în spatele obstacolelor, în zona de umbră geometrică.

Difracția reprezintă fenomenul de ocolire de către lumină a obstacolelor care au dimensiuni comparabile cu lungimea de undă a luminii. Undele difractate vor interfera, rezultând franje luminoase mai complicate, formate din maxime și minime de intensitate.

Rețeaua de difracție este un dispozitiv optic ce constă într-un sistem de fante înguste, rectilinii, paralele, egale, echidistante și foarte apropiate una de alta.

Ea se realizează prin trasarea pe o placă transparentă de plexiglas a unui număr N de zgârieturi rectilinii pe o distanță L.

Intervalele transparente dintre zgârieturi reprezintă fantele rețelei.

Notăm cu

r₁,r₂ – distanțele parcurse de cele două unde de la fante până în punctul P, unde analizăm interferența
l – distanța dintre fante
D - distanța de la fante la ecran
x – distanța de la centrul ecranului (O) până la punctul P
Δr = r₂ – r₁ = diferența de drum geometric
δ = n ∙ Δr = drum optic

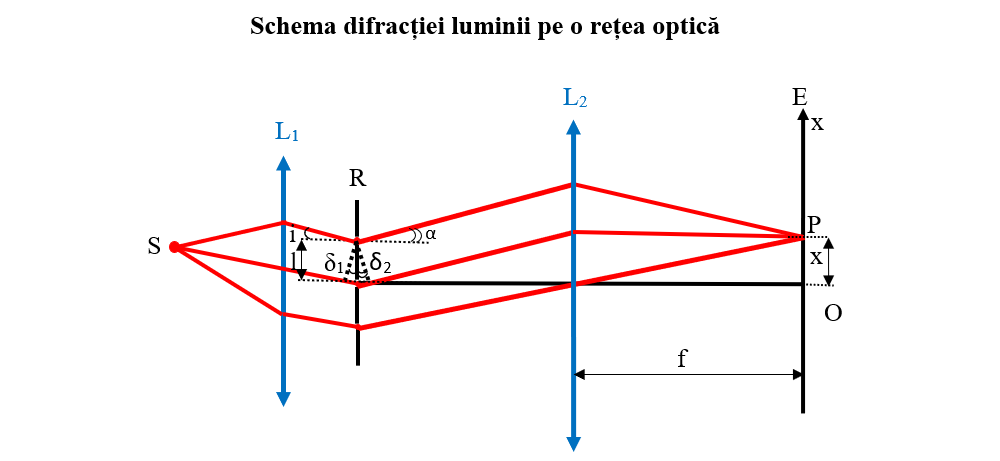
Un fascicul de lumină monocromatică, provenit de la sursa S, este transformat într-un fascicul paralel de către lentila L1 și care cade sub un unghi de incidență, i, pe rețeaua de difracție, R.

Figura de difracție se vede pe ecranul E. Imaginea de difracţie prezintă un maxim central, urmat de o succesiune de maxime şi minime de ordin superior cu intensități ce descresc din ce în ce mai mult.

Conform Principiului Huygens- Fresnel, fiecare fantă a rețelei devine sediul unor unde secundare coerente care formează cu axa optică AO unghiul α.

Între aceste unde va exista mereu aceeași diferență de drum optic:
δ = δ₁ – δ₂.

Diferența de drum optic între undele incidente pe rețea este:
δ₁ = l ∙ sin i.

Diferența de drum optic între undele difractate de rețea este:
δ₂ = l ∙ sin α.

δ = δ₁ – δ₂ = l ( sin i – sin α)

În cazul rețelei de difracție, fenomenul este mai complicat deoarece are loc atât difracția undelor secundare (de pe fante), cât și interferența tuturor undelor secundare. Cum sunt N trăsături pe rețea, vor interfera între ele N fascicule.

Prin interferența undelor provenite de la două fante aflate la distanța l pe rețea, vom obține în punctul P un maxim dacă δ = k ∙ λ și un minim când δ = (2k + 1) ∙ λ

Având în vedere fenomenul de interferență al celor N fascicule putem spune că în toate direcțiile pentru care:
δ = l ( sin i ± sin α) ∙ λ, avem maxime de difracție.

🔦 Observație

a) În fenomenul de difracție maximele nu vor avea aceeași intensitate, ci vor scădea în intensitate cu creșterea ordinului k.

b) Dacă iluminăm rețeaua cu lumină albă, relația: δ = l ( sin i ± sin α) ∙ λ ne arată că pentru un k dat, diversele lungimi de undă λ vor avea maximul de intensitate sub diferite unghiuri α, astfel încât pe ecranul E se va forma spectrul continuu al fasciculului incident.

Astfel, rețeaua de difracție este un instrument spectral cu care se analizează compoziția luminii unei surse.

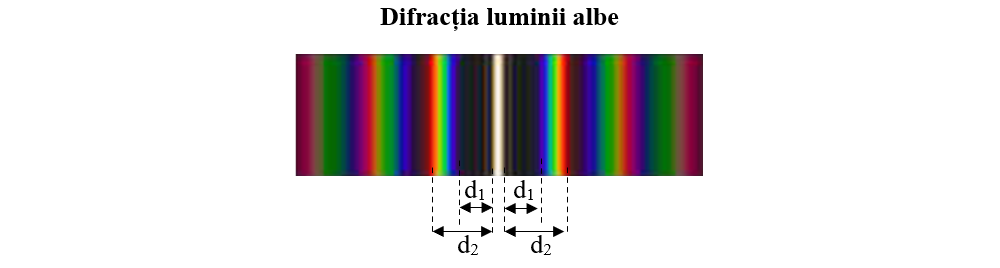
Pe ecran se formează o franjă centrală albă, întrucât în dreptul acestui maxim k = 0 și atunci și δ = 0 , pentru toate lungimile de undă.

Pentru k = 1 se obțin maxime de ordinul întâi.

Spectrele de difracție de ordine diferite sunt dispuse de ambele părți ale franjei centrale, având liniile cu λ mai mici situate mai aproape de franja centrală.

Observăm că lângă franja centrală albă apare, de o parte și de alta, linia violetă și mai departe linia roșie, întrucât lumina violetă are lungimea de undă mai mică decât lumina roșie.

Numărul total de franje față de maximul central:

N = [ 2 k_max + 1], unde k_max = k pentru un unghi α = ± π/2

Determinarea lungimii de undă cu ajutorul rețelei de difracție

Pentru a determina lungimea de undă a unei lumini cu ajutorul rețelei de difracție se așază pe bancul optic laserul, lentila convergentă cu o anumită distanță focală (f = +120 mm), rețeaua de difracție și ecranul.

În unele montaje se mai poate intercala o lentilă convergentă între rețea și ecran.

Având în vedere fenomenul de interferență al celor N fascicule, putem spune că în toate direcțiile pentru care avem
δ = l(sin i ± sin α) = k λ, vom obține un maxim de difracție.

Pentru un unghi de incidență i = 0, obținem:
l sin α = k λ

În cazul unghiurilor de difracție mici:

Astfel punctul P în care se va forma maximul de ordinul k se va afla la distanța:

Această formulă ne permite să calculăm lungimea de undă a luminii folosite (a unui laser de o anumită culoare sau a unui bec prevăzut cu un filtru de o anumită culoare) determinând experimental distanța x pe ecran și cunoscând distanța focală a lentilei folosite (f) și constanta rețelei (n).

👀 Experiment: Difracția luminii

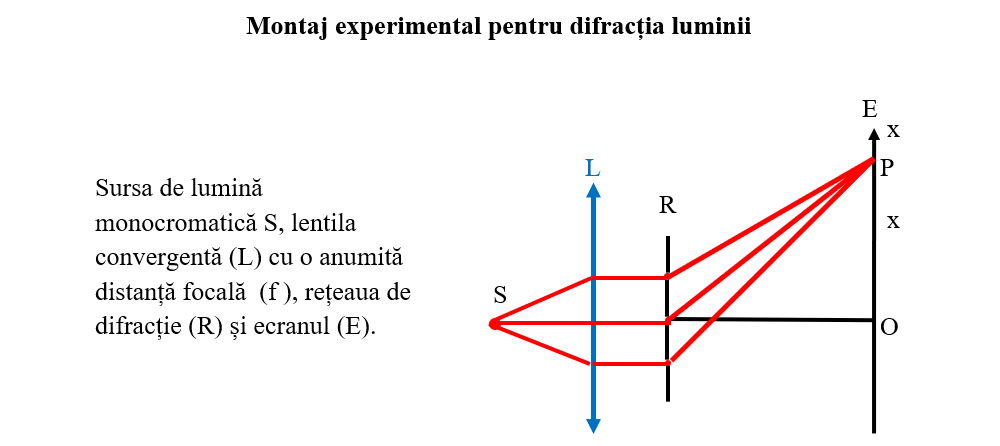
Pentru a determina lungimea de undă a unei lumini cu ajutorul rețelei de difracție se așază pe bancul optic sursa de lumină S (laserul), lentila convergentă (L) cu o anumită distanță focală (f), rețeaua de difracție (R) și ecranul (E).

• Se măsoară distanța de la maximul central de pe ecran (0) până la primul maxim luminos de pe ecran (x) pentru care k = 1;

• Se notează distanța focală a lentilei folosite și constanta rețelei de difracție (n);

• Se aplică formula de calcul a lungimii de undă:

👀 Experiment: Difracția luminii în viața de zi cu zi

• Un mod ușor de a observa difracția luminii este de a aduce degetul mare foarte aproape de degetul arătător (fără a le atinge). Privind prin fanta acestora spre un bec puternic vom vedea niște linii negre subțiri ce apar între cele două degete, paralele cu degetele. Acestea sunt franje de interferență, locuri unde lumina interferează constructiv și distructiv, producând zone luminoase și întunecoase.

• Există o limită naturală pentru claritatea unei imagini, după ce aceasta a trecut printr-un sistem optic (cristalinul ochilor noștri, lentilă etc.), numită limita de difracție. De exemplu, când privim un obiect îndepărtat, imaginea acestuia este blurată (neclară, “ în ceață”, fără contur clar), deoarece ochii noștri au o rezoluție limitată datorită mărimii pupilelor (diafragma ochilor) noastre. Cu cât deschidem mai mult pupilele pentru a intra cât mai multă lumină, cu atât undele luminoase care trec prin ele sunt mai blurate, datorită difracției lor. La fel ca în cazul ochilor și în fotografii efectele de difracție blurează imaginea finală, astfel încât nu există o fotografie perfectă.

• Dacă privim o sursă de lumină îndepărtată printr-o pânză de umbrelă, observăm o serie de irizații (colorări). Acest lucru se datorează fenomenului de difracție a luminii prin spațiile dintre fibre care au dimensiuni foarte mici. Irizațiile apar datorită maximelor laterale (colorate) de difracție în lumină albă.

• Difracția luminii pe un DVD duce la formarea unui curcubeu în direcția discului datorită bandei spiralate cu spațiere foarte mică de pe suprafața acestuia.

• Hologramele de pe cardurile bancare (și pe o varietate largă de produse) au la bază tot difracția luminii pe o rețea care să producă un șablon de difracție dorit. Ele sunt elemente de securitate contra falsurilor (sunt greu de reprodus, necesitând echipamente scumpe pentru multiplicare) . Fiecare punct al hologramei captează fasciculele de lumină din toate punctele obiectului. Fiecare fragment al hologramei conține întreaga imagine a obiectului.

• Difracția atmosferică conduce la apariția unui halo, un inel strălucitor în jurul Soarelui sau Lunii, când privim acești aștrii prin nori subțiri ce conțin cristale de gheață.

• Culoarea roșiatică pe care o capătă Soarele la răsărit și la apus se datorează difracției luminii în particulele atmosferice.

• Difracția luminii este utilizată pentru a determina structurile substanțelor.

• Spectroscopul are la bază difracția luminii, determinând lungimea de undă a surselor de lumină. Astfel, cercetătorii descoperă elementele componente ale stelelor. Dependența unghiului α sub care se obține maximul de difracție de ordinul k, de lungimea de undă a radiației permite determinarea lungimii de undă prin măsurarea poziției maximelor de difracție.