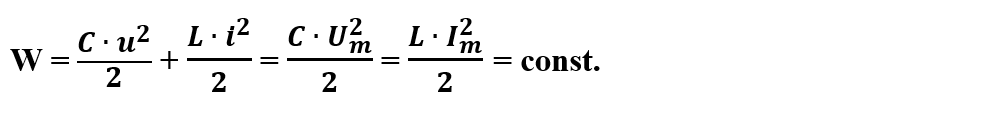II.2.2. Analogia unui circuit oscilant LC cu un oscilator elastic.
Analogia unui circuit oscilant LC cu un oscilator elastic:
1) De la t = 0 la T/4 :
- După ce condensatorul este încărcat de la sursă, se comută K din poziția 1 în poziția 2.
- La momentul inițial t = 0, condensatorul este încărcat la tensiunea Ucm, energia circuitului fiind energie electrică înmagazinată de condensator We = C ∙ U2/2.
- Condensatorul începe descărcarea și tensiunea la bornele sale scade.
- Curentul electric ce trece prin bobină determină apariția unui câmp magnetic a cărui inducție crește la o valoare maximă pe măsură ce intensitatea curentului din circuit crește.
- Prin bobină continuă să treacă curent până la descărcarea completă a condensatorului, caz în care tensiunea pe armăturile acestuia este zero.
- În mod analog, oscilatorul mecanic are inițial elongație maximă și energie potențială maximă, Ep = k ∙ A2/2 . Lăsat liber, energia lui potențială scade în timp ce crește energia lui cinetică, suma lor rămânând constantă.
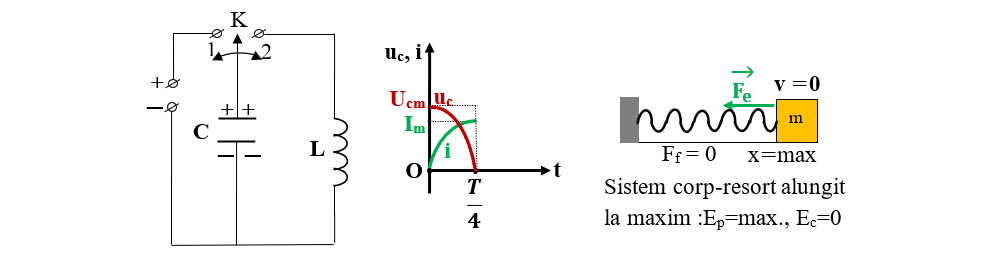
2) De la t = T/4 la T/2 :
- Chiar dacă tensiunea pe armăturile condensatorului și cea la bornele bobinei este zero, bobina menține prin autoinducție trecerea curentului.
- La momentul t = T/4 condensatorul s-a descărcat complet, curentul de descărcare are valoare maximă.
- Energia circuitului este sub formă de energie magnetică WB = L ∙ Im2/2 .
- Bobina va genera o t.e.m. de autoinducție, care va deplasa electronii în același sens și se concentrează pe armătura care anterior a fost pozitivă.
- Condensatorul se reîncarcă în sens invers celui inițial.
- În cazul oscilatorului mecanic, datorită inerției, el depășește poziția de echilibru, schimbându-se sensul deformării. În momentul trecerii prin poziția de echilibru are energie cinetică maximă : Ec = m ∙ vm2/2 .
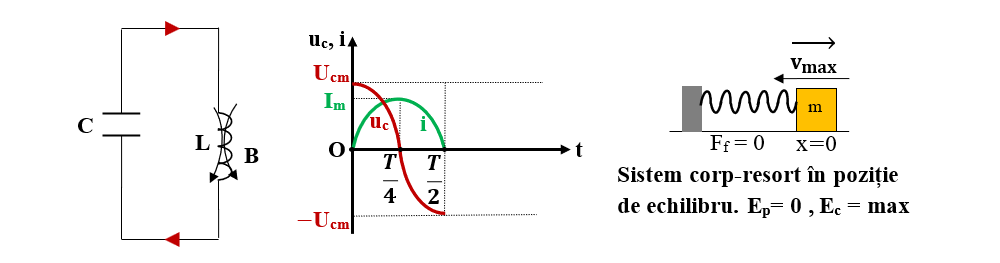
3) De la t = T/2 la 3T/4 :
Condensatorul este încărcat la aceeași tensiune maximă, dar în sens invers situației inițiale.
Curentul prin circuit se anulează datorită apariției unui câmp magnetic variabil, dar de sens opus situației anterioare.
Analog, oscilatorul mecanic va avea elongație maximă de sens opus celei inițiale, fiind comprimat la maxim. El are energie potențială maximă, Ep = k ∙ A2/2 .
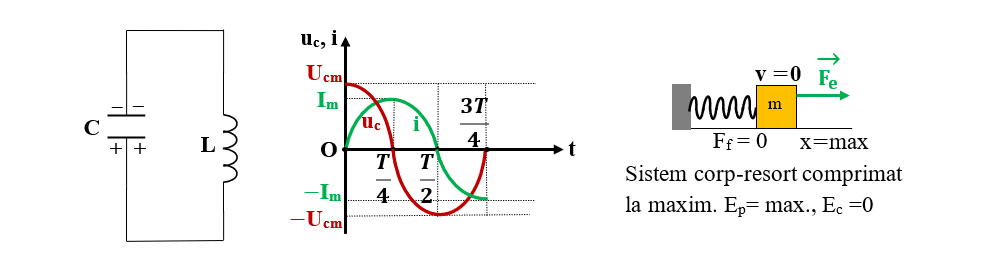
4) De la t = 3T/4 la T :
Chiar și după ce tensiunea pe condensator devine nulă, bobina este parcursă de un curent de autoinducție, în același sens cu cel determinat de descărcarea condensatorului. Aceasta duce la descărcarea condensatorului cu o polaritate inversă.
După un timp egal cu perioada oscilației T, întregul proces se reia.
În cazul oscilatorului mecanic, datorită inerției, el depășește poziția de echilibru, schimbându-se sensul deformării. În momentul trecerii prin poziția de echilibru are energie cinetică maximă : Ec = m ∙ vm2/2 .
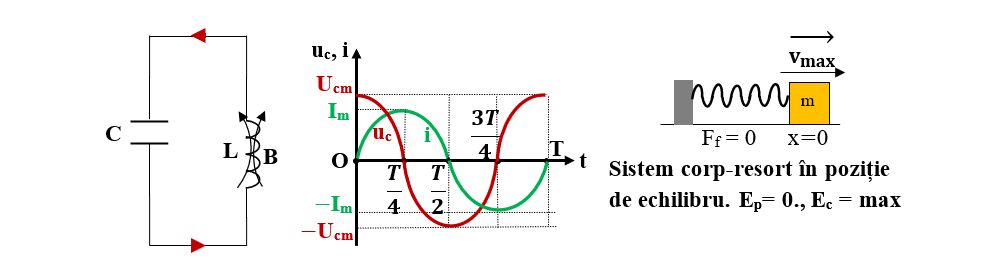
Comportarea unui circuit LC ideal ce nu pierde energie prin efect Joule este similară celei a unui oscilator mecanic liniar armonic (oscilator elastic sau pendul gravitațional). Din acest motiv, circuitul LC se numește circuit oscilant.
Producerea oscilațiilor electromagnetice libere într-un circuit oscilant se datorează transformării succesive a energiei circuitului din energie a câmpului electric în energie a câmpului magnetic.
În cazul oscilatorului mecanic are loc transformarea succesivă a energiei sistemului din energie potențială în energie cinetică.
În ambele tipuri de oscilatori se consideră că energia totală se conservă, cu amplitudini de oscilație constante în timp.
Energia totală a unui circuit oscilant ideal, la un moment dat, este dată de suma dintre energia câmpului electric dintre armăturilor condensatorului și energia câmpului magnetic din bobină: