III.1.2. Legea inducției electromagnetice.

Legea inducției electromagnetice:

Tensiunea electromotoare indusă (e) într-un circuit este proporțională cu viteza de variație a fluxului magnetic inductor prin acel circuit.

unde:
ΔΦ este variația fluxului magnetic inductor
Δt este intervalul de timp în care are loc variația fluxului magnetic inductor

Semnul minus ține cont de regula lui Lenz:

Tensiunea electromotoare indusă are un astfel de semn încât fluxul câmpului magnetic pe care îl produce curentul indus, se opune variației fluxului magnetic inductor.

Legea inducției electromagnetice pentru o bobină cu N spire are expresia:

Legea inducției electromagnetice pentru un conductor deplasat perpendicular pe liniile de câmp magnetic are expresia:

e = B ∙ l ∙ v

unde:
B = inducția câmpului magnetic
l = lungimea conductorului rectiliniu
v = viteza constantă de deplasare a conductorului în câmpul magnetic

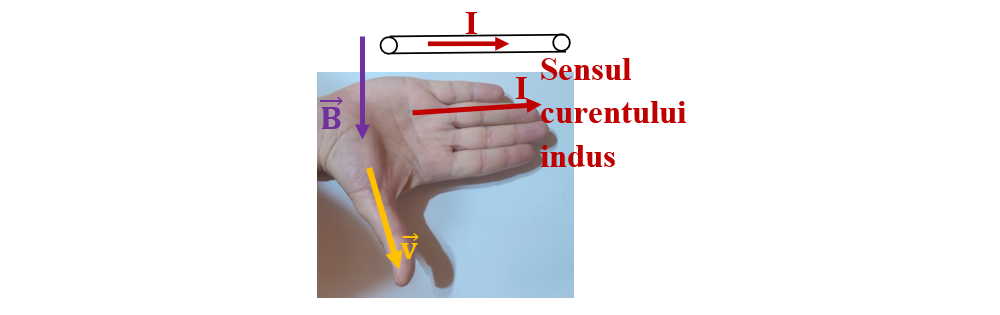
Sensul curentului indus în conductorul deplasat perpendicular pe liniile de câmp magnetic se determină cu regula mâinii drepte : se așază mâna dreaptă în lungul conductorului, astfel încât vectorul B să intre în palmă, iar degetul mare întins lateral să fie în sensul vitezei conductorului.

Cele patru degete întinse vor indica sensul curentului indus.

Deducerea legii inducției electromagnetice

Se consideră un conductor de lungime l care se deplasează sub acțiunea unei forțe exterioare Fʹ, perpendicular pe liniile de câmp magnetic și cu viteza v constantă.

Asupra conductorului parcurs de curent electric se va exercita o forță electromagnetică F egală în modul cu forța exterioară Fʹ, dar de sens opus (viteza conductorului este constantă).

Tensiunea electromotoare indusă (e) este dată de raportul dintre lucrul mecanic Lʹ efectuat de forța exterioară Fʹ pentru deplasarea sarcinii electrice și sarcina electrică q:

Lucrul mecanic Lʹ efectuat de forța Fʹ = F = B ∙ I ∙ l este:
Lʹ = B ∙ I ∙ l ∙ x

Produsul l ∙ x este aria măturată de conductor în timpul deplasării pe distanța x. Această arie poate fi exprimată ca o diferență dintre două arii: aria S₂ delimitată de circuit când conductorul este în poziție finală și aria S₁, delimitată de circuit când conductorul este în poziție inițială.

l ∙ x = S₂ – S₁

Lʹ = B ∙ I ∙ (S₂ – S₁) = I ∙ (B ∙ S₂ – B ∙ S₁) = I ∙ Φ₂ – I ∙ Φ₁ = I ∙ ΔΦ