II.8. Gruparea rezistoarelor.
Orice element de circuit (generator electric, bec, rezistor, motor, întrerupător) poate fi legat (grupat) cu un altul (de același fel sau diferit) în două moduri:
-
În serie și
-
În paralel.
În viața de zi cu zi întâlnim grupări mixte de serie cu paralel.
Un grup de rezistoare se înlocuiește cu unul singur, denumit rezistor echivalent. Rezistența acestuia reprezintă echivalentul rezistențelor respectivei grupări.
👀 Experiment: Gruparea în serie a rezistoarelor
Materiale necesare:
Baterie electrică, rezistoare de diferite valori ( 50 Ω, 100 Ω ), fire de legătură, ampermetru, voltmetru (multimetru).
Descrierea experimentului:
- Realizează următorul montaj legând în serie cele 2 rezistoare.
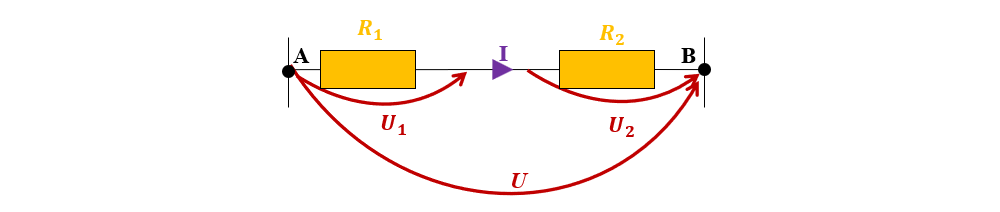
- Aplică o tensiune de la baterie și măsoară intensitatea curentului electric, tensiunea de la capetele grupării și tensiunea pe fiecare rezistor.
- Calculează raportul dintre tensiunea de la capetele grupării și intensitatea ce trece prin ele, adică rezistența electrică a grupării celor două rezistoare. În ce relație se află cele trei tensiuni măsurate, respectiv rezistența grupării cu rezistențele celor 2 rezistoare ?
Tensiunea dintre capetele grupării de rezistoare este egală în acest caz cu suma tensiunilor de la bornele celor două rezistoare.
Se observă că suma rezistențelor celor două rezistoare este egală cu rezistența grupării de rezistoare.
Concluzia experimentului:
Aplicând la capetele rezistorului echivalent aceeași tensiune ca la bornele grupării în serie, prin rezistorul echivalent circulă același curent ( I ) ca prin gruparea echivalată: U = U1 + U2 .
Se poate scrie:
U1 = IR1; U2 = IR2 ; U = IRs ;
U = U1 + U2
IRs = IR1 + IR2
Rs = R1 + R2
Rezistoarele prin care trece același curent și care se află pe aceeași latură a unui circuit formează o grupare în serie, fiind echivalate cu rezistorul Rs .
Rezistența echivalentă a unei grupări serie de rezistoare este egală cu suma rezistențelor fiecărui rezistor:
Rs = R1 + R2

👀 Experimentul 19: Gruparea în paralel a rezistoarelor
Materiale necesare:
Baterie electrică, rezistoare de diferite valori ( 50 Ω, 100 Ω ), fire de legătură, ampermetru, voltmetru (multimetru).
Descrierea experimentului:
- Realizează următorul montaj legând în paralel cele două rezistoare.

- Aplică o tensiune de la baterie și măsoară intensitatea curentului electric ce trece atât prin fiecare rezistor, cât și prin circuitul cu sursa.
- Măsoară tensiunea electrică de la capetele grupării și tensiunea pe fiecare rezistor.
- Calculează rapoartele dintre intensitate și tensiune (adică inversele rezistențelor electrice dintre punctele de măsurare) pentru fiecare dintre cele trei măsurători.
- În ce relație se află cele trei intensități măsurate? Dar cele trei tensiuni măsurate?
Suma inverselor celor două rezistențe este egală cu inversul rezistenței circuitului. Intensitatea curentului ce intră în grupare este egală cu suma intensităților curenților ce trec prin cele două rezistoare, iar tensiunile măsurate sunt egale.
Concluzia experimentului:
Aplicând la capetele rezistorului echivalent aceeași tensiune ca la bornele grupării în paralel, pe rezistorul echivalent va cădea aceeași tensiune ca pe fiecare dintre rezistoarele din grupare: U = U1 = U2.
Se poate scrie:

Simplificând pe U de la numărător obținem formula rezistenței echivalente paralel.
Rezistoarele care se află pe laturi diferite între aceleași două noduri ale unui circuit, având aceeași tensiune la capete formează o grupare în paralel, fiind echivalate cu rezistorul Rp.
Inversul rezistenței echivalente a unei grupări paralel de rezistoare este egal cu suma inverselor rezistențelor fiecărui rezistor:


🔓 Probleme rezolvate
1. Determină rezistenţa echivalentă a rezistoarelor din următoarea grupare mixtă:
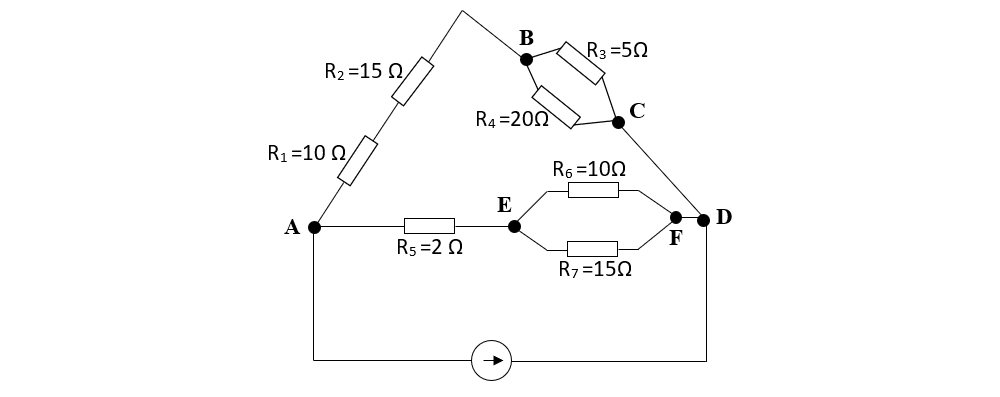
Rezolvare:
Se notează pe rețea toate nodurile cu litere mari.
Mergem pe conturul circuitului de la un nod la altul și echivalăm grupările de rezistoare cu rezistoarele echivalente, serie sau paralel:
Între nodul A și B avem 2 rezistoare pe aceeași latură, deci sunt în serie și le echivalăm cu Rs1.
Între nodul B și C avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu Rp1.
Între nodul A și E avem 1 rezistor pe care îl copiem.
Între nodul E și F avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu Rp2.

Calculăm rezistențele echivalente:

Pe schema nouă, continuăm să echivalăm grupările de rezistoare:
Între nodul A și D, pe latura de sus, avem 2 rezistoare pe aceeași latură (Rs1 cu Rp1), deci sunt în serie și le echivalăm cu Rs2 .
Între nodul A și D, pe latura din mijloc, avem 2 rezistoare pe aceeași latură (R5 cu Rp2), deci sunt în serie și le echivalăm cu Rs3 .
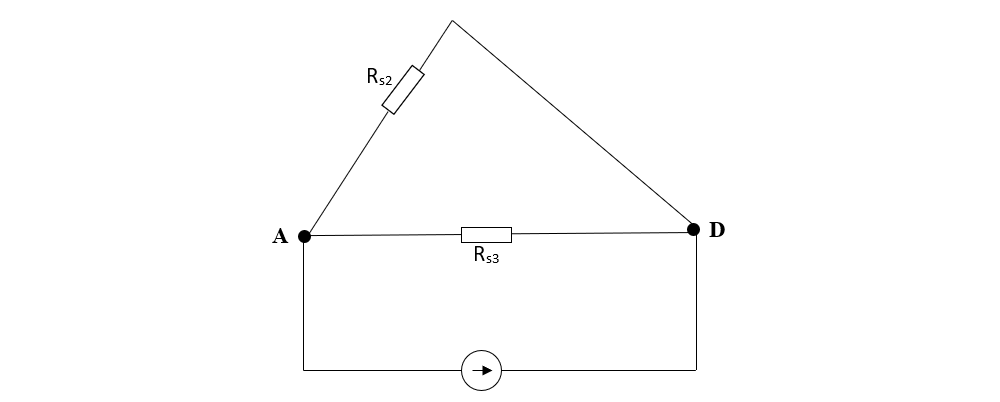
Calculăm rezistențele echivalente:
Rs2 = Rs1 + Rp1 = 25 + 4 = 29Ω
Rs3 = R5 + Rp2 = 2 + 6 = 8Ω
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:
Între nodul A și D avem 2 rezistoare pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu Rp3.

Calculăm rezistența echivalentă:
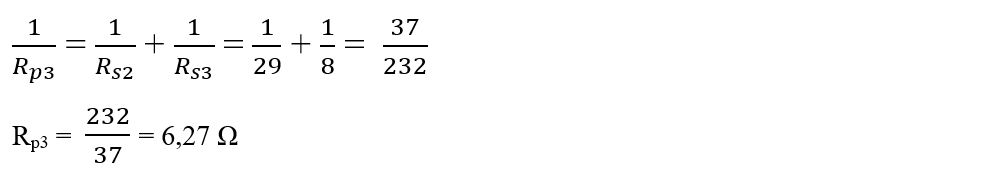
2. Determină rezistenţa echivalentă a rezistoarelor din următoarea grupare mixtă:

Rezolvare:
Notăm pe rețea toate nodurile cu litere mari.
Mergem pe conturul circuitului de la un nod la altul și echivalăm grupările de rezistoare cu rezistoare echivalente, serie sau paralel:
Între nodul A și B, în partea stângă, avem 2 rezistoare pe aceeași latură (R1 și R2), deci sunt în serie și le echivalăm cu Rs1.
Între nodul A și B avem 2 rezistoare pe aceeași latură (R4 și R7), deci sunt în serie și le echivalăm cu Rs2.
Între nodul B și C avem 1 rezistor (R3), pe care îl copiem.
Între nodul A și C avem 2 rezistoare pe aceeași latură (R5 și R6), deci sunt în serie și le echivalăm cu Rs3.
Între nodul B și C avem sursa pe care o copiem.

Calculăm rezistențele echivalente:
Rs1 = R1 + R2 = 2 + 3 = 5Ω
Rs2 = R4 + R7 = 7 + 13 = 20Ω
Rs3 = R5 + R6 = 10 + 6 = 16Ω
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:
Între nodul A și B avem 2 rezistoare (Rs1 și Rs2) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu Rp1.
Restul schemei o copiem.

Calculăm rezistența echivalentă:

Pe schema nouă, continuăm să echivalăm grupările de rezistoare:
Între nodul B și C avem 2 rezistoare (Rp1 și Rs3) pe aceeași latură, deci sunt în serie și le echivalăm cu Rs4.
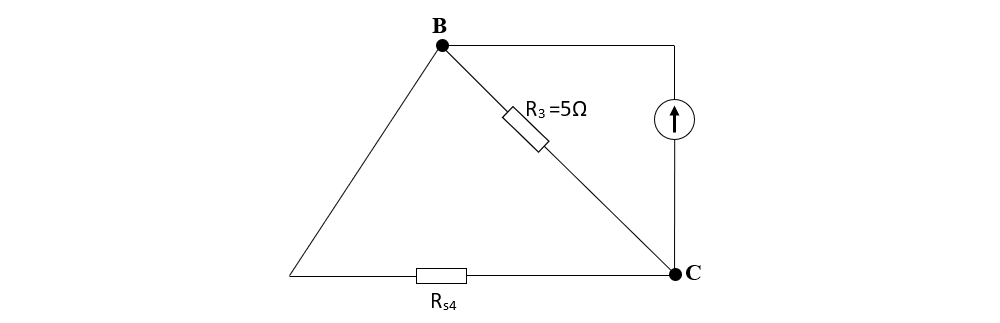
Calculăm rezistența echivalentă:
Rs4 = Rp1 + Rs3 = 4 + 16 = 20Ω
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:
Între nodul B și C avem 2 rezistoare (Rs4 și R3) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu Rp2.
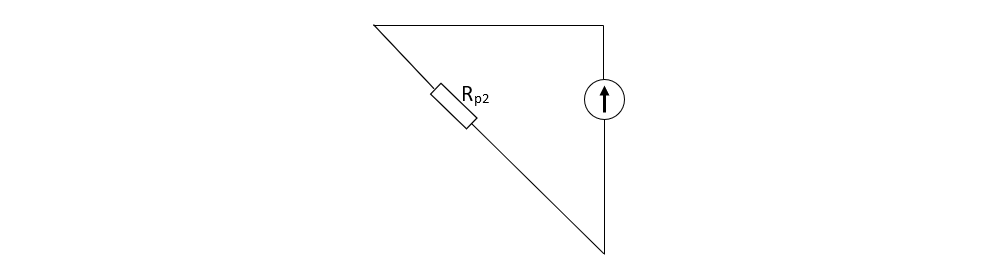
Calculăm rezistența echivalentă a întregii grupări:
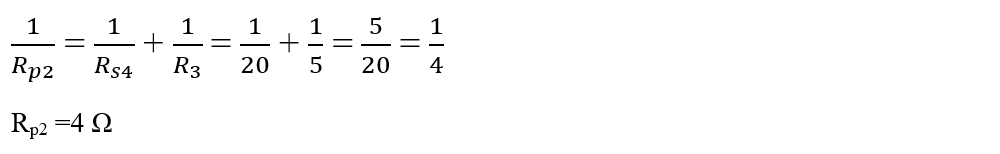
3. Determină intensitățile curenților din următorul circuit ramificat:
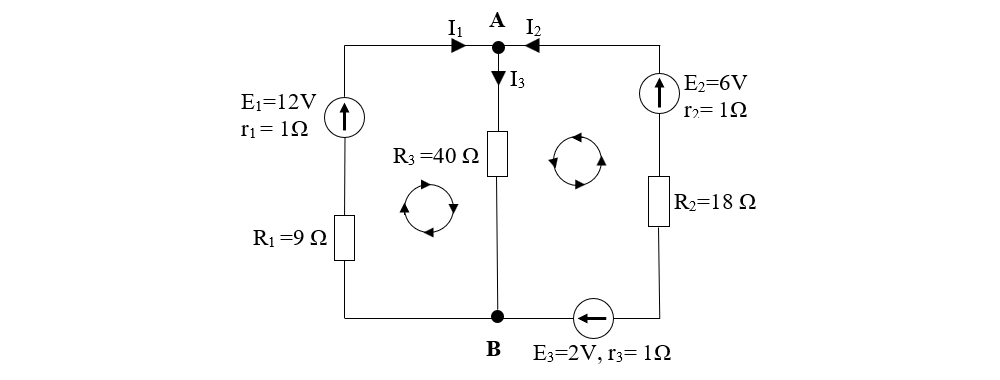
Rezolvare:
Notăm cu litere mari nodurile rețelei (A și B).
Notăm laturile rețelei, stabilim arbitrar sensurile curenților de pe fiecare latură:
AE1B (I1)
AE2B (I2)
AR3B (I3)
Notăm ochiurile simple ale rețelei. Stabilim arbitrar (cum dorim) câte un sens de parcurs pentru fiecare ochi (orar sau antiorar).
Aplicăm prima teoremă a lui Kirchhoff:
“Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul respectiv“.
Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea, în cazul nostru pentru un singur nod:
I1 + I2 = I3
Aplicăm a doua teoremă a lui Kirchhoff:
“Suma algebrică a tensiunilor electromotoare pentru un ochi de circuit este egală cu suma algebrică a căderilor de tensiune din acel ochi de circuit“, pentru două ochiuri simple:

Facem un sistem de 3 ecuații și cu cele trei necunoscute I1, I2, I3.

Înlocuim datele numerice:

Scoatem pe I1 din prima ecuație:
I1 = I3 – I2 și îl înlocuim în a doua ecuație
12 = (I3 – I2) ∙ 10 + I3 ∙ 40 = I3 ∙ 50 – I2 ∙ 10
Rezolvăm sistemul cu 2 ecuații și 2 necunoscute, prin reducere:

Înlocuim pe I3 într-o ecuație cu I2:

Schimbăm sensul curentului I2 ales inițial, arbitrar, pe rețea:

Din prima ecuație îl aflăm pe I1:
I1 = I3 – I2 = 0,2 – (–0,2) = 0,4 A
4. Becurile B2 și B3 au valorile nominale de 6 V și 0,1 A și funcționează normal. Ampermetrul indică 300 mA. Este identic becul B1 cu becurile B2 și B3 ?
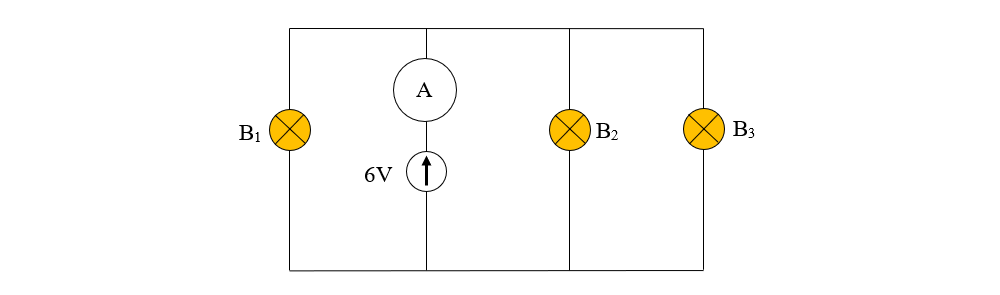
Rezolvare:
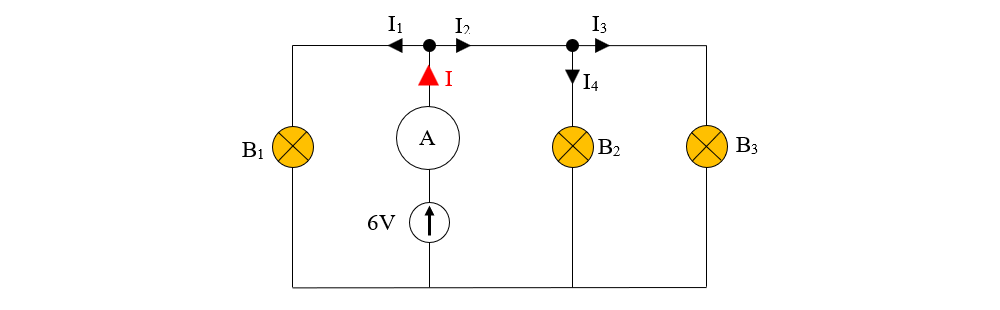
I = I1 + I2 = 0,3 A
I2 = I3 + I4 = 0,2 A
I3 = I4 = 0,1 A
I1 = 0,1 A
Curentul din ramura principală cu sursa și cu ampermetrul se ramifică pe laturile becurilor B2 și B3, care fiind identice și legate în paralel, vor avea fiecare un curent de intensitate egală cu jumătate din curentul I2, adică 0,1 A.
Becul B1 are tensiunea nominală de 6 V și intensitatea nominală de I1 = 0,1 A.
Deci becul B1 este identic cu becurile B2 și B3.