II.7. Legile lui Kirchhoff.
Elementele rețelelor electrice (circuitelor ramificate):
1. Nodul de circuit reprezintă intersecția a cel puțin trei conductoare electrice.
2. Latura de circuit este porțiunea de circuit cuprinsă între două noduri succesive, astfel încât prin elementele ei să circule același curent electric.
3. Ochiul de circuit reprezintă porțiunea de circuit formată din cel puțin două laturi, conectate astfel încât să formeze un contur închis (linie poligonală închisă).
🔓 Cum se rezolvă o problemă cu rețea electrică:
-
Notează cu litere mari nodurile rețelei (punctele unde se intersectează și se ating cel puțin trei conductori).
-
Notează laturile rețelei (porțiunile de circuit dintre două noduri succesive, prin care trece un singur curent). Stabilește arbitrar (cum dorești tu) câte un sens pentru fiecare curent și notează-i cu simboluri cu indici (I1, I2, ... etc). Ai grijă ca unii să intre în nod (vârful săgeții spre nod) și alții să iasă din nod (vârful săgeții opus nodului).
-
Notează ochiurile simple ale rețelei (porțiunile de circuit care au un contur închis și formate din două laturi). Stabilește arbitrar (cum dorești tu) câte un sens de parcurs pentru fiecare ochi.
Prima lege a lui Kirchhoff :
“Suma algebrică a intensităților curenților care se întâlnesc într-un nod de circuit este nulă“.

unde intensitățile Ik pot fi pozitive sau negative, în funcție de modul în care trece curentul prin nod (intră în nod sau iese din nod).
O altă modalitate de enunțare a primei legi a lui Kirchhoff:
“Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul de rețea“.
Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea.
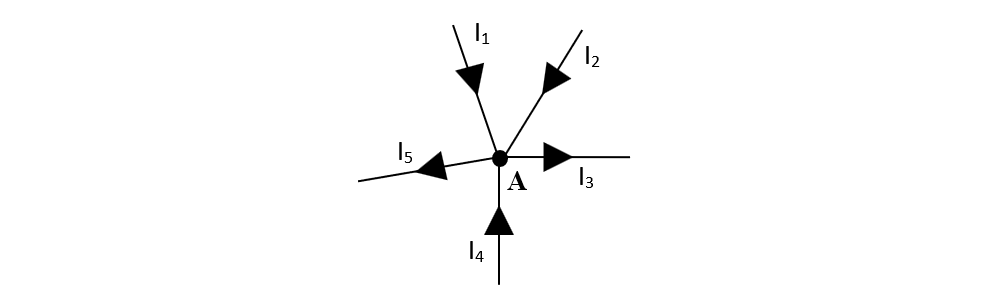
De exemplu pentru nodul A aplicăm Teorema I a lui Kirchhoff:
I1 + I2 + I4 = I3 + I5
A doua lege a lui Kirchhoff:
“Suma algebrică a tensiunilor electromotoare dintr-un ochi de rețea este egală cu suma algebrică a tensiunilor de pe fiecare latură din acel ochi de circuit“.

unde termenii sumelor pot fi pozitivi sau negativi, în funcție de sensul tensiunii sau al intensității în raport cu sensul ales arbitrar pentru ochiul considerat.
Pentru m = nr. ochiuri simple, se scriu m ecuații cu a doua teoremă a lui Kirchhoff.
Convenții de semne
a) Tensiunea electromotoare
- se ia cu plus dacă sensul curentului electric prin sursă este identic cu cel al ochiului ales arbitrar : + E

- se ia cu minus dacă sensul curentului electric prin sursă este opus cu cel al ochiului ales arbitrar : - E

b) Tensiunea electrică (produsul rezistenței laturii cu intensitatea din acea latură):
- se ia cu plus dacă sensul curentului electric este același cu cel al ochiului ales arbitrar (sens de referință): + I ∙ R

- se ia cu minus dacă sensul curentului electric este opus cu cel al ochiului ales arbitrar (sens de referință): - I ∙ R

🔓 Problemă rezolvată
1. Determină intensitățile curenților din următorul circuit ramificat:
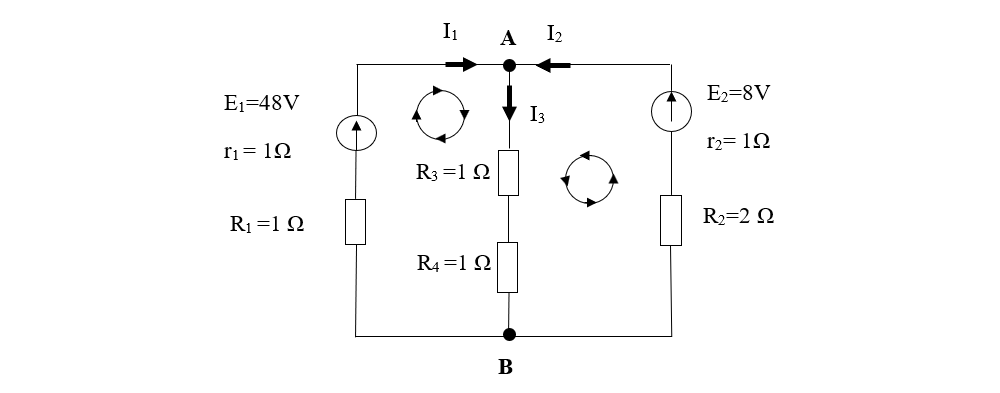
Rezolvare:
Notăm cu litere mari nodurile rețelei (A și B).
Notăm laturile rețelei, stabilim arbitrar sensurile curenților de pe fiecare latură:
AE1B (I1)
AE2B (I2)
AR3B (I3)
Notăm ochiurile simple ale rețelei. Stabilim arbitrar (cum dorim) câte un sens de parcurs pentru fiecare ochi (orar sau antiorar).
Aplicăm prima teoremă a lui Kirchhoff: “Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul respectiv“.
Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea, deci pentru un singur nod:
I1 + I2 = I3
Aplicăm a doua teoremă a lui Kirchhoff: “Suma algebrică a tensiunilor electromotoare pentru un ochi de circuit este egală cu suma algebrică a căderilor de tensiune din acel ochi de circuit“, pentru două ochiuri simple:

Facem un sistem de 3 ecuații și cu cele trei necunoscute I1, I2, I3

Înlocuim datele numerice:

Scoatem pe I1 din prima ecuație: I1 = I3 – I2 și îl înlocuim în a doua ecuație
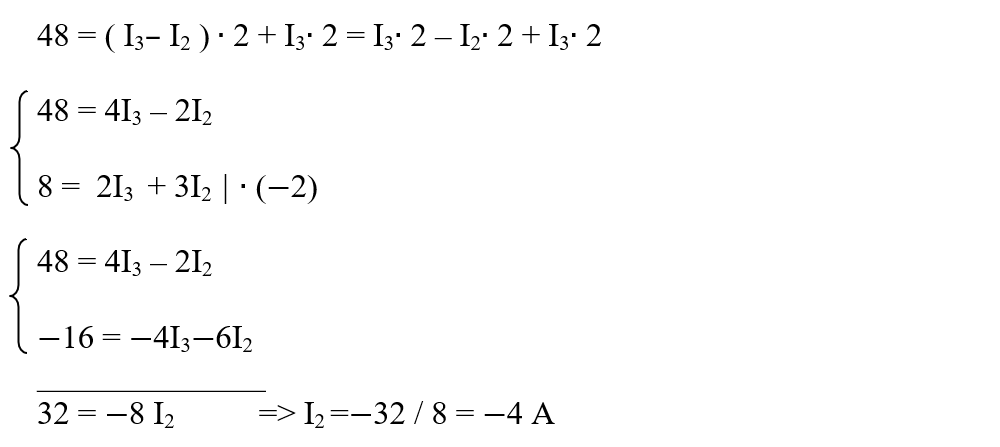
Când un curent dă negativ, i se schimbă sensul ales arbitrar și se înlocuiește în celelalte ecuații cu minus.
Se înlocuiește I2 într-o ecuație cu I3:
3 ∙ (-4) + 2 I3 = 8
I3 = 10 A
Din prima ecuație îl aflăm pe I1:
I1 = 10 - (- 4) = 14 A