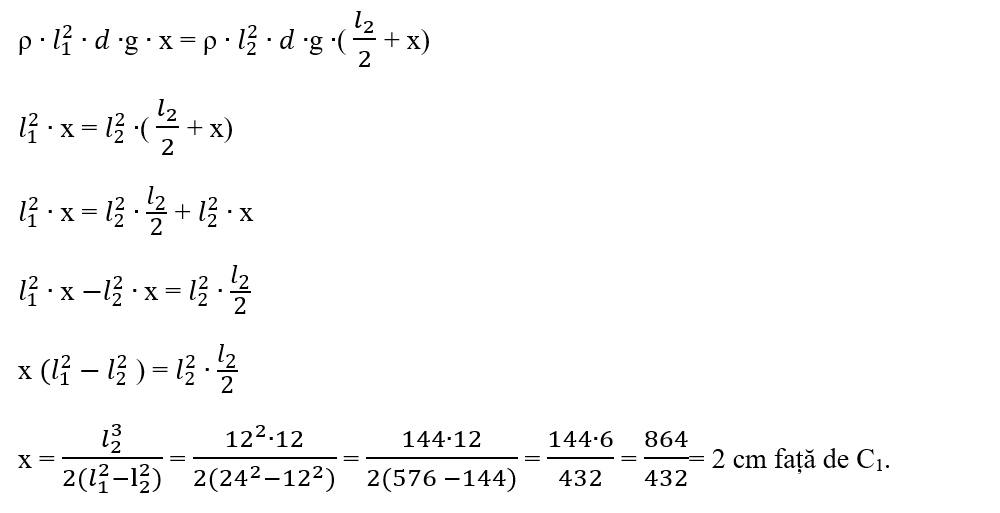V.4.3. Determinarea centrului de greutate al corpurilor neomogene și de formă neregulată.

Pentru corpurile cu formă geometrică neregulată, centrul lor de greutate se determină experimental.

👀 Experiment: Determinarea centrului de greutate
🔥 Atenție când lucrezi cu obiecte ascuțite!
🔥 Atenție când lucrezi cu acul să nu te înțepi!

Materiale necesare:
Bucată de carton, foarfecă, creion, fir cu plumb (poți face firul cu plumb dintr-un fir de care legi o piuliță), ață cu ac

Descrierea experimentului:

• Decupează cartonul într-o formă dorită de tine.
• Alege trei puncte de pe marginea conturului, perforează-le cu vârful unui compas şi prinde-le câte un fir de aţă de 10 cm.
• Ține figurina suspendată de unul dintre fire şi trasează cu creionul verticala prin punctul de susţinere cu ajutorul firului cu plumb (piuliţă). Poţi trasa uşor verticala dacă prinzi de un perete cele două fire – al figurinei şi al piuliţei, cu bandă adezivă.
• Repetă operaţia şi cu celelalte două fire.

  La intersecţia celor trei verticale notează punctul C, numit centru de greutate al corpului.

🔓 Probleme rezolvate

1. Dintr-un disc circular omogen cu raza R = 10 cm se taie un disc cu raza r = 5 cm, tangent interior la discul mare. Să se determine poziția centrului de greutate al porțiunii rămase.

Rezolvare:

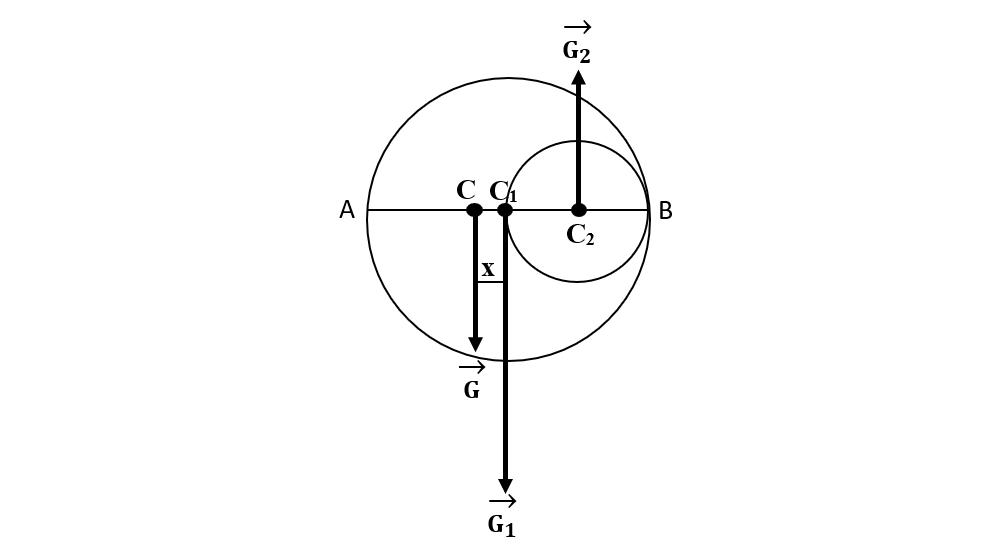
La un cerc centrul de greutate este chiar în centrul cercului, adică la o distanță egală cu raza cercului față de marginea acestuia.

Discul mare are centrul de greutate în C₁, la care R = C₁A = 10 cm.
Discul mic are centrul de greutate în C₂, la care r = C₂B = 5 cm.
Porțiunea decupată va avea centrul de greutate în C, la distanța x față de C₁ și va reprezenta punctul de aplicație al greutății G, care este rezultanta forțelor G₁ și G₂.
Deoarece porțiunea circulară este decupată, ea va avea greutatea G₂ opusă greutății G₁ (va trebui scăzută din greutatea totală, G₁).

Punem condiția echilibrului de rotație astfel încât momentul forței G₁ față de C să fie egal cu momentul forței G₂ față de C.
M_G1 = M_G2
G₁ ∙ x = G₂ ∙ (r + x)

Notăm cu d = grosimea plăcii pentru a putea calcula greutatea celor două discuri:
G₁ = m₁ ∙ g = ρ ∙ V₁ ∙ g = ρ ∙ S₁ ∙ d ∙ g = ρ ∙ π ∙ R² ∙ d ∙ g
G₂ = m₂ ∙ g = ρ ∙ V₂ ∙ g = ρ ∙ S₂ ∙ d ∙ g = ρ ∙ π ∙ r² ∙ d ∙ g

Înlocuim aceste valori în condiția de echilibru de rotație:
ρ ∙ π ∙ R² ∙ d ∙ g ∙ x = ρ ∙ π ∙ r² ∙ d ∙ g ∙ (r + x)
R² ∙ x = r² ∙ (r + x)
R² ∙ x = r² ∙ r + r² ∙ x
R² ∙ x - r² ∙ x = r² ∙ r
x ∙ (R² - r²) = r² ∙ r

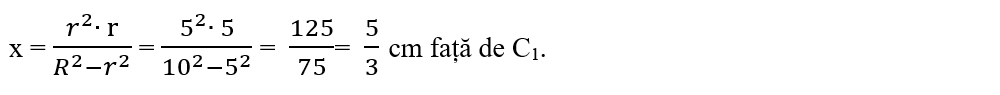
2. Dintr-o placă pătrată omogenă și de grosime, d, constantă, având latura de l₁ = 24 cm se taie un pătrat cu latura l₂ = 12 cm. Să se determine poziția centrului de greutate al porțiunii rămase.

Rezolvare:

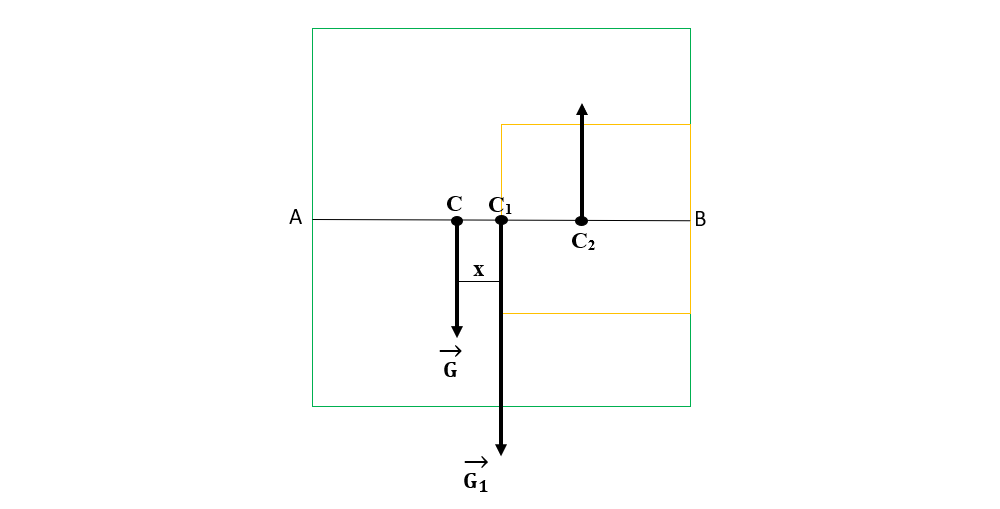
La un pătrat centrul de greutate este în intersecția diagonalelor, adică la o distanță egală cu jumătate din latura sa față de marginea acestuia.

Pătratul mare are centrul de greutate în C₁, la care C₁A = 12 cm.
Pătratul mic are centrul de greutate în C₂, la care C₂B = 6 cm.
Porțiunea decupată va avea centrul de greutate în C, la distanța x față de C₁ și va reprezenta punctul de aplicație al greutății G, care este rezultanta forțelor G₁ și G₂.
Deoarece pătratul mic este decupat, el va avea greutatea G₂ opusă greutății G₁ (va trebui scăzută din greutatea totală, G₁).

Punem condiția echilibrului de rotație astfel încât momentul forței G₁ față de C să fie egal cu momentul forței G₂ față de C.

Notăm cu d = grosimea plăcii pentru a putea calcula greutatea celor două discuri:
G₁ = m₁ ∙ g = ρ ∙ V₁ ∙ g = ρ ∙ S₁ ∙ d ∙ g = ρ ∙ l₁² ∙ d ∙ g
G₂ = m₂ ∙ g = ρ ∙ V₂ ∙ g = ρ ∙ S₂ ∙ d ∙ g = ρ ∙ l₂² ∙ d ∙ g

Înlocuim aceste valori în condiția de echilibru de rotație: