IV.8.2. Ciocniri perfect elastice.
Un caz particular al ciocnirilor este ciocnirea perfect elastică, în care deformările corpurilor dispar după ciocnire și energia cinetică, transformată în timpul ciocnirii în energie potențială elastică, se restituie integral în energie cinetică după ciocnire.
Ciocnirea este perfect elastică dacă :
- Energia cinetică a corpurilor se conservă prin ciocnire:
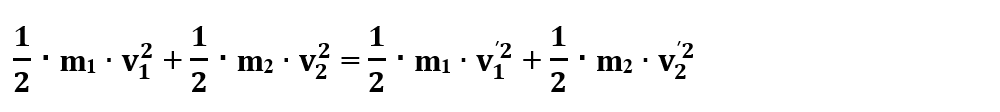
- Impulsul total se conservă:
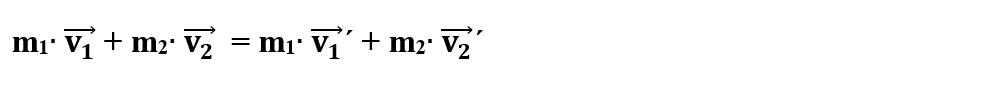
🔦 Observație
Ciocnirile perfect elastice sunt modele idealizate de ciocniri, în realitate existând mici variații ale energiei interne și ale geometriei inițiale. În cazul unor ciocniri ușoare dintre bile de oțel sau de fildeș, cărucioare prevăzute cu tampoane-resorturi elastice se pot aproxima ca ciocniri perfect elastice.

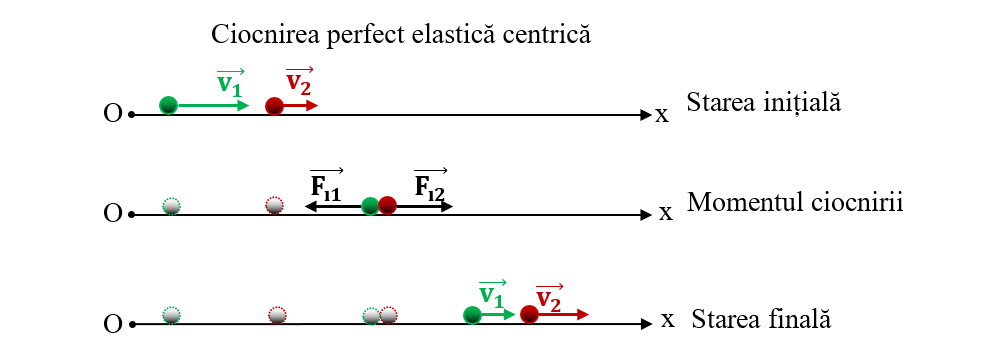

Pentru a rezolva acest sistem, trecem termenii care conțin pe m1 în stânga și pe cei care conțin pe m2 în dreapta egalității. Astfel obținem:
m1 ∙ (v12 - vʹ12) = m2 ∙ (vʹ22) - v22)
m1 ∙ (v1 - v1́ )(v1 + v1́ ) = m2 ∙ (v2ʹ - v2)(v2ʹ+ v2)
m1 ∙ (v1 - v1́ ) = m2 ∙ (v2ʹ - v2)
Împărțim membru la membru ultimele două ecuații și obținem:
v1 + v1́ = v2ʹ+ v2
vrʹ= - vr
În ciocnirile perfect elastice unidimensionale avem:
v1́ - v2ʹ= -(v1 - v2)
vrʹ= - vr
vrʹ= v1́ - v2ʹ, este viteza relativă a bilei 1 față de bila 2 după ciocnire
vr = v1 - v2, este viteza relativă a bilei 1 față de bila 2 înainte de ciocnire
În concluzie, în ciocnirea perfect elastică unidimensională a două bile, prima bilă se apropie de cea de-a două cu o viteză relativă vr = v1 - v2, o lovește și se întoarce înapoi cu o viteză relativă vrʹ= v1́ - v2ʹ, egală în modul dar de semn schimbat.
Din următoarele două ecuații aflăm vitezele celor două bile după ciocnirea lor perfect elastică, unidimensională:
v1́ - v2ʹ= -(v1 - v2)
m1 ∙ v1 + m2 ∙ v2 = m1 ∙ v1ʹ + m2 ∙ v2ʹ

Cazuri particulare:
1) Când bila 2 este în repaus înainte de ciocnire (v2 = 0), obținem:

În acest caz bila 2 va căpăta o viteză v2́ în sensul în care este lovită, în timp ce bila 1 se poate întoarce înapoi dacă masa sa m1 este mai mică decât a celei de-a doua bile.
Cazuri particulare:
2) Când bila 2 este în repaus înainte de ciocnire (v2 = 0) și are aceeași masă cu bila 1, obținem:
m1 = m2
v1́ = 0
v2́ = v1
În acest caz bila 2 preia tot impulsul și energia primei bile și bila 1 se oprește.
👀 Experiment: Ciocnirea perfect elastică a două bile cu aceeași masă
Materiale necesare:
Bile de aceeași masă.
Modul de lucru:
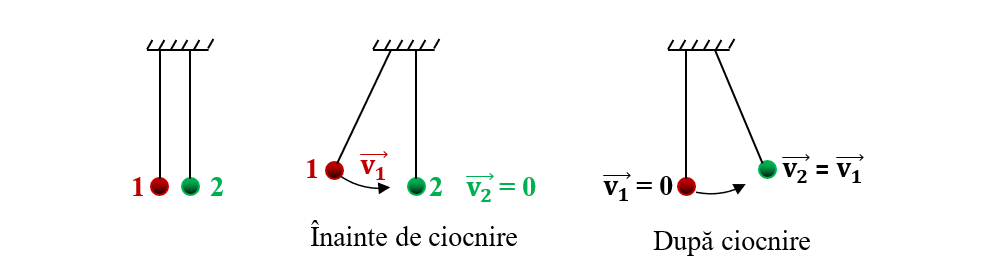
- Suspendăm două bile identice pe fire paralele.
- Deviem într-o parte o bilă și îi dăm drumul ca să ciocnească cealaltă bilă.
Observăm că bila deviată se oprește și bila lovită este deviată identic cu prima. După aceasta, bila a doua se întoarce înapoi și o lovește pe prima și așa mai departe până ce mișcarea oscilatorie se stinge datorită frecării cu aerul atmosferic.
Ciocnirea dintre corpuri este un fenomen mecanic în care impulsurile corpurilor variază brusc, fiind o interacțiune de durată foarte scurtă.
Ciocnirea este perfect elastică dacă :
- Energia cinetică a corpurilor se conservă prin ciocnire:
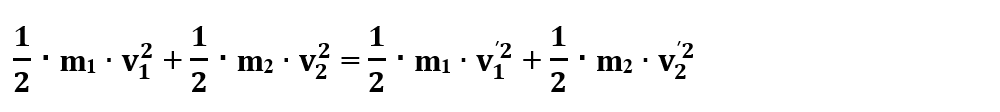
- Impulsul total se conservă:
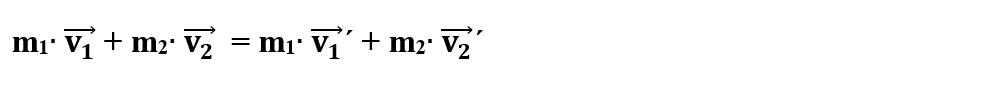
Când cele două bile au masele egale (m1 = m2 = m) și bila 2 este în repaus înainte de ciocnire (v2 = 0) și obținem:

Cazuri particulare:
3) Când bila 2 are masa mult mai mare decât bila 1:
m2 ≫ m1
Pornim de la formula generală și simplificăm primul termen cu m2 și vom obține:

Deoarece m2 ≫ m1, termenul care conține raportul m1/m2 se poate neglija, fiind aproape zero pentru m2 extrem de mare.
v1́ ≈ 2 ∙ v2 - v1
v2́ = 0
Când bila 2 este în repaus înainte de ciocnire (v2 = 0) și are masa mult mai mare decât bila 1, bila 1 foarte ușoară se întoarce înapoi (ricoșează) cu aceeași viteză pe care a avut-o înainte de ciocnire, în timp ce bila 2 masivă rămâne în repaus.
v1́ = - v1
v2́ = 0
Acest caz descrie ciocnirea perfect elastică a unui corp cu un perete rigid. Așa explicăm apariția unei presiunii pe pereții vaselor, ca urmare a variației de impuls a moleculelor care lovesc continuu pereții vasului.
👀 Experiment: Ciocnirea perfect elastică a două bile cu mase diferite
Materiale necesare:
Bile de diferite mase.
Modul de lucru:
Cazul 1:
Când bila 2 (cea în repaus) are masa mult mai mare decât bila 1 (bila deviată), adică m2 ≫ m1:
- Suspendăm două bile cu mase mult diferite pe fire paralele.
- Deviem într-o parte bila foarte ușoară și îi dăm drumul ca să ciocnească cealaltă bilă masivă, aflată în repaus.
Observăm că bila ușoară (1) este deviată înapoi și bila masivă (2) rămâne în repaus și după ciocnire.
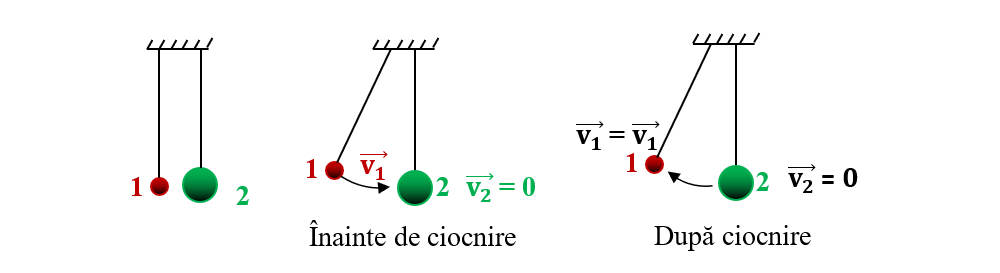
Când bila 2 este în repaus înainte de ciocnire (v2 = 0) și are masa mult mai mare decât bila 1, bila 1 foarte ușoară se întoarce înapoi (ricoșează) cu aceeași viteză pe care a avut-o înainte de ciocnire, în timp ce bila 2 masivă rămâne în repaus.
v1́ = - v1
v2́ = 0
Acest caz descrie ciocnirea perfect elastică a unui corp cu un perete rigid.
Cazul 2:
Când bila 2 (cea aflată în repaus) are masa mult mai mică decât bila 1 (cea care este deviată)
- Deviem într-o parte o bilă masivă (1) și îi dăm drumul ca să ciocnească cealaltă bilă ușoar�ă aflată în repaus (2).
Observăm că bila ușoară (2) este deviată de bila mai grea și bila masivă (1) își continuă mișcarea.
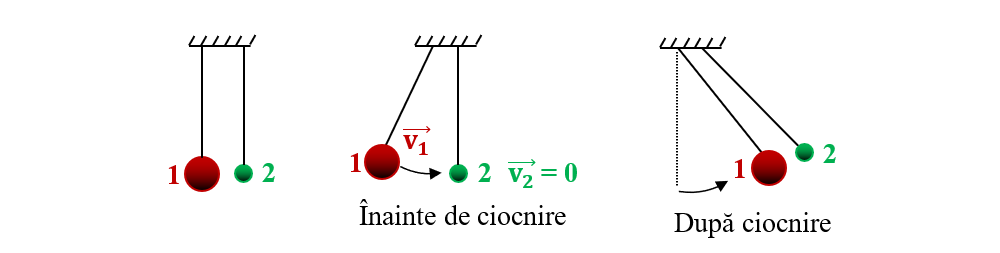
Când bila 2 este în repaus înainte de ciocnire (v2 = 0) și are masa mult mai mică decât bila 1, după ciocnire, bila 1 masivă continuă drumul în partea opusă cu o viteză mai mică față de cea care a avut-o înainte de ciocnire. O parte din energia cinetică inițială a bilei masive este transferată bilei ușoare, care este deviată în același sens cu bila grea.
🔓 Problemă rezolvată
1. O bilă de 200 g lovește frontal un perete cu viteza de 3 m/s. Determină forța medie care apare în timpul ciocnirii, știind timpul de contact cu peretele de 2 ms. Cât este forța medie când bila lovește oblic peretele ?
Rezolvare:
Scriem datele problemei:
m = 200 g = 0,2 kg
v = 3 m/s
Δt = 2 ms = 0,002 s
Fm = ?
Scriem teorema de variație a impulsului mecanic

Deoarece ciocnirea este perfect elastică, avem:

Deci, forța exercitată asupra bilei din partea peretelui este perpendiculară pe perete și de sens opus cu viteza inițială:

Când bila lovește oblic peretele, variația impulsului se obține prin scăderea vectorială:

