IV.1.2. Lucrul mecanic al unei forțe cu modul variabil.

Când forța și deplasarea au aceeași direcție și același sens, dar modulul forței variază în timpul deplasării punctului său de aplicație, lucrul mecanic este definit prin produsul dintre forța medie (F_m) și deplasarea (d):

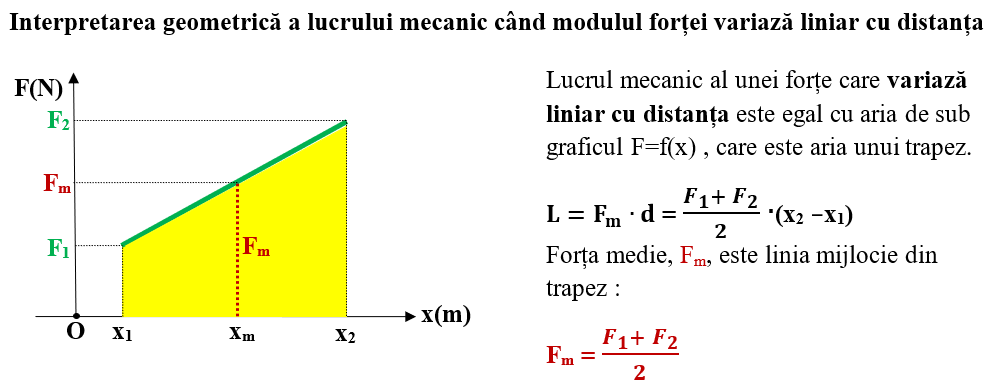
L = F_m ∙ d = F_m ∙ (x₂ – x₁)

1. Când forța variază liniar cu distanța, forța medie este media aritmetică a forțelor în punctul de start și în cel de oprire și avem expresia lucrului mecanic:

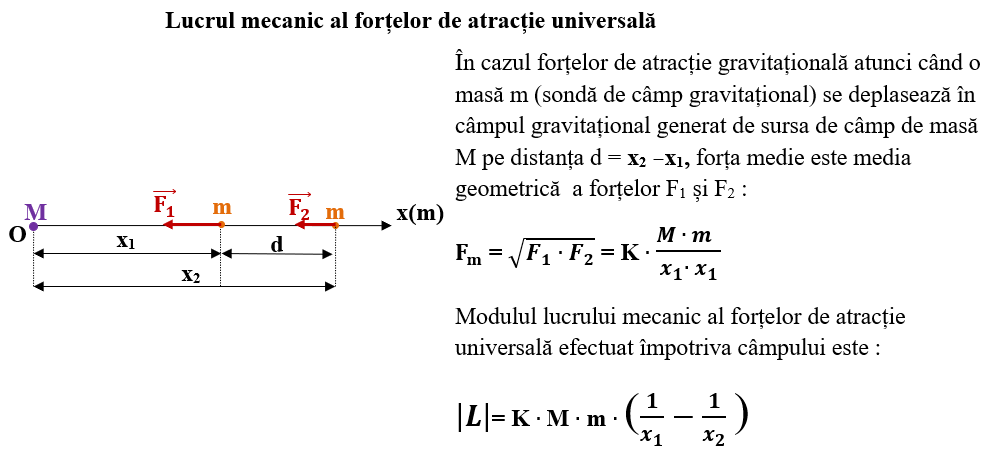
2. Când forța este invers proporțională cu distanța, forța medie este media geometrică a valorilor forțelor în punctul de plecare și cel de oprire și avem expresia lucrului mecanic:

🔓 Probleme rezolvate

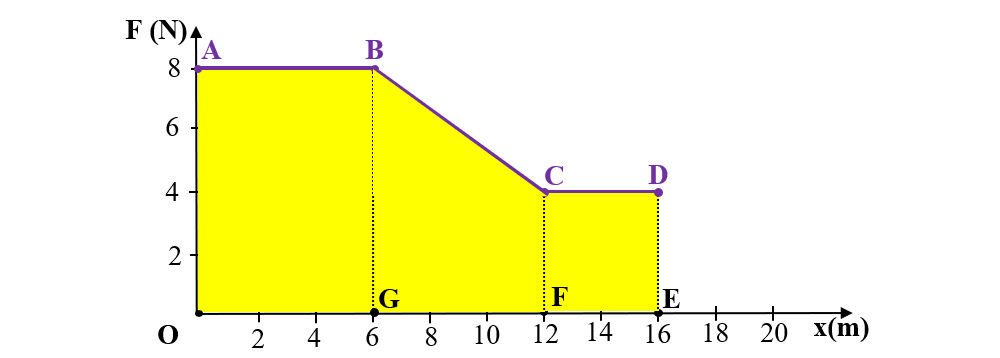
1. O forță F ce se exercită asupra unui corp variază în funcție de deplasarea punctului său de aplicație ca în graficul următor. Ce lucru mecanic efectuează forța pe intervalul [0m;16m]?

Rezolvare:

Lucrul mecanic al forței F este egal cu aria suprafeței OABCDEO, care este egală cu suma ariilor dreptunghiului OABG, trapezului BCFG și pătratului CDEF.

Știind că aria dreptunghiului este produsul lungimii cu lățimii și că aria trapezului este produsul înălțimii cu suma bazelor, totul împărțit la 2, avem:

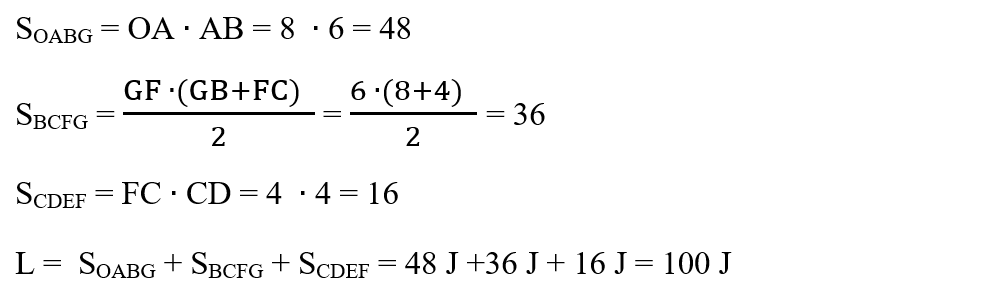
2. O forță F ce se exercită asupra unui corp variază în funcție de deplasarea punctului său de aplicație după legea F = 2x. Ce lucru mecanic efectuează forța între punctele A(2;4) și B(4;8)? Ce interpretare geometrică poți să dai lucrului mecanic al unei forțe variabile ?

Rezolvare:

Se reprezintă grafic forța F (N) în funcție de distanța x (m):
Pentru x = 1 m → F = 2 ∙ 1 = 2 N
Pentru x = 2 m → F = 2 ∙ 2 = 4 N
Pentru x = 3 m → F = 2 ∙ 3 = 6 N
Pentru x = 4 m → F = 2 ∙ 4 = 8 N

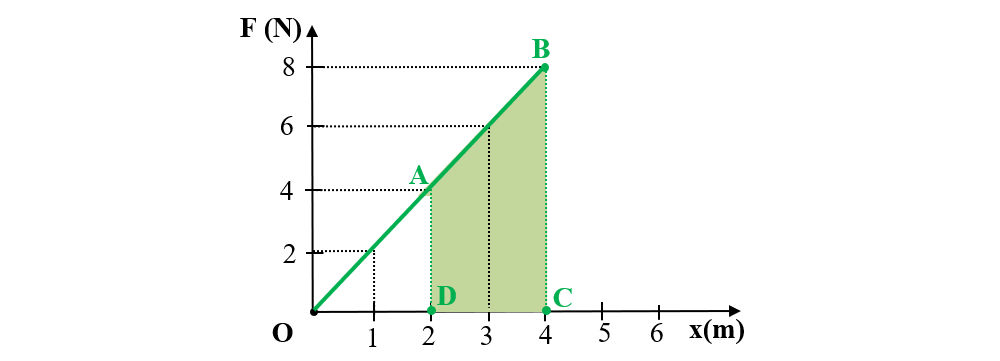
Lucrul mecanic al forței F între punctele A(2;4) și B(4;8) este egal cu aria trapezului ABCD. Știind că aria trapezului este produsul înălțimii cu suma bazelor, totul împărțit la 2, avem:

Știind formula lucrului mecanic al unei forțe variabile care este direct proporțională cu deplasarea, L = F_m ∙ (x₂ – x₁), observăm că forța medie este media aritmetică a valorilor inițială și finală a forței: