III.7.3. Câmpul gravitațional.
Forța gravitațională se manifestă la distanță prin intermediul câmpului gravitațional.
Câmpul gravitațional este un câmp vectorial care descrie forța gravitațională care acționează asupra unui obiect în orice punct dat din spațiu, pe unitatea de masă.
Intensitatea câmpului gravitațional (Γ) într-un punct este egală cu raportul dintre forța ce acționează din partea câmpului asupra unui corp aflat în acel punct și masa corpului.
În Sistemul Internațional, intensitatea câmpului gravitațional se măsoară în m/s2.

F – forța de atracție gravitațională dintre sursa de câmp cu masa M și corpul de probă cu masa m.
Modulul intensității câmpului gravitațional este direct proporțional cu masa M a sursei și invers proporțional cu pătratul distanței (r) față de sursă:

La suprafața unei planete intensitatea câmpului gravitațional este egală cu accelerația gravitațională la suprafața planetei, g0.
Pentru Pământ avem:

Câmpul gravitațional este:
- un câmp vectorial, deoarece i se poate atașa un sistem de vectori, și anume vectorul de intensitate a câmpului;
- un câmp radial, deoarece liniile de câmp au direcție radială;
- un câmp staționar, deoarece intensitatea câmpului este constantă în timp;
- un câmp cu simetrie sferică.
Orice câmp se reprezintă prin linii de câmp. Linia de câmp este o linie imaginară la care vectorii intensitate ai câmpului sunt tangenți în orice punct.
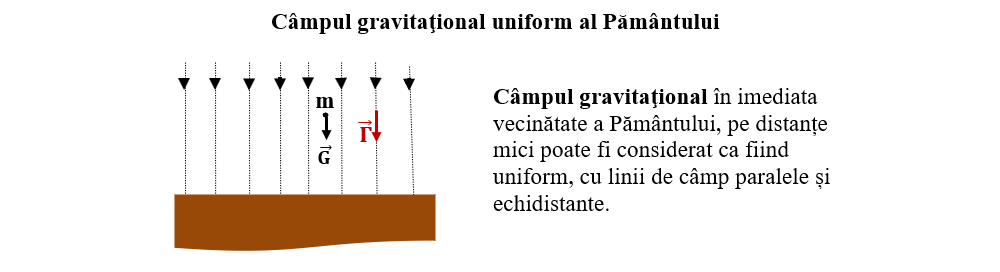
Într-o zonă mică de pe suprafața Pământului, unde liniile de câmp pot fi considerate paralele și echidistante, câmpul este uniform.
Se numeşte câmp gravitaţional o regiune din spaţiu, limitată sau nelimitată, unde în fiecare punct se face simţită acţiunea unei forţe gravitaţionale de atracţie determinate în modul, direcţie şi sens.
🔦 Observații
- Câmpurile de forţe în general (câmpul gravitaţional în particular) sunt o formă de existenţă a materiei, distinctă de substanţă, care fac posibilă transmiterea din aproape în aproape a interacţiunilor dintre corpuri.
- Corpul care generează câmpul gravitaţional se numeşte sursă a câmpului.
- Masa corpului, ca o măsură a capacităţii sale de a genera un câmp gravitaţional sau de a suporta acţiunea unui câmp gravitaţional se numeşte masă gravitaţională sau masă grea. Experimental s-a constatat că ea este numeric egală cu masa inertă.
- Câmpul gravitaţional creat de corpul de masă M există chiar în absenţa corpului de probă din punctul P. Numai plasând acest corp de probă, de masă m, putem detecta prezenţa câmpului.
- Direcţia vectorului intensitate a câmpului gravitaţional este radială, iar sensul spre centrul corpului, de masă M, generator de câmp gravitaţional.

În tabelul următor sunt prezentate valorile intensității câmpului gravitațional (accelerației gravitaționale) la suprafața Soarelui, Lunii și a celor nouă planete din sistemul nostru solar:

🔓 Problemă rezolvată
1. Calculează forța de atracție dintre Pământ și Lună.
Se dau: Distanța medie Pământ-Lună = 3,8 ∙ 108 m Masa Pământului ≅ 6 ∙ 1024 kg, Masa Lunii = 7,3 ∙ 1022 kg și Constanta atracției universale = 6,67 ∙ 10-11 N ∙ m2/kg2.
Rezolvare:
Aplicăm legea atracției universale:
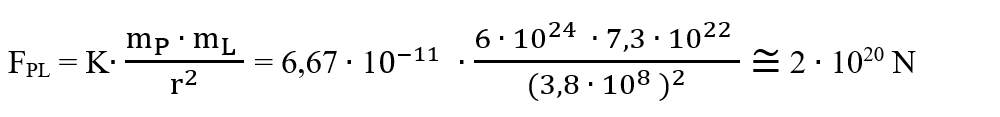
2. Să se calculeze cu cât la sută scade intensitatea câmpului gravitațional la înălțimea h = 100 km, dacă la suprafața Pământului valoarea sa este Γ(R0) ≅ 9,8 m/s2 și raza Pământului este de 6357 km.
Rezolvare:
Γ(R0) = g0 ≅ 9,8 m/s2
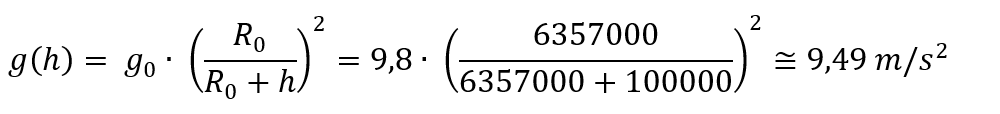
Δg = g0 - g = 9,8 m/s2 - 9,49 m/s2 = 0,31 m/s2 = 3,1 % ∙ g0
3. Un corp este aruncat în câmpul gravitațional al Pământului, de la înălțimea h = 1960 m, cu o viteză inițială de 2 m/s, paralelă cu suprafața Pământului.
Se cere:
a) Timpul de cădere pe sol, tc.
b) Viteza cu care atinge solul, v (tc).
c) Distanța de la proiecția inițială pe sol până la punctul de impact cu solul, numită bătaia, xb.
d) Ecuația traiectoriei.
Rezolvare:
a) Întrucât înălțimea de la care este aruncat corpul nu este foarte mare, neglijăm variația intensității câmpului cu altitudinea și considerăm că
Γ(h + R0) = Γ(R0) = g0 ≅ 9,8 m/s2.
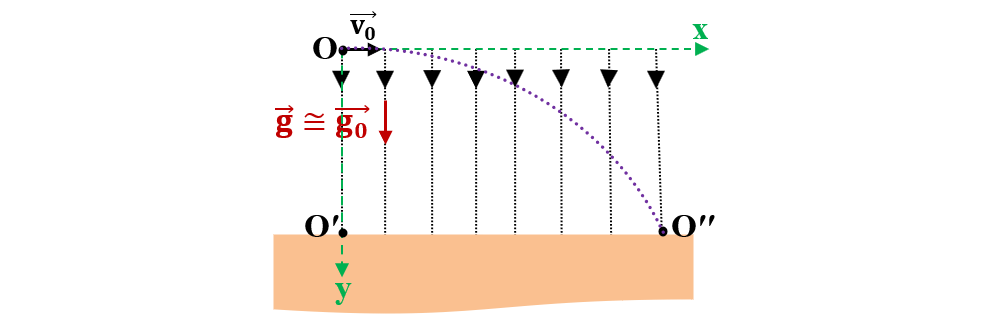
Alegem un sistem de coordonate Oxy și studiem mișcările proiecțiilor punctului material pe axele Ox și Oy, scriind legile accelerației, vitezei și spațiului pentru fiecare axă:
Ox : ax = 0; vx = v0; x = v0 ∙ tc
Oy : ay = g0; vy = g0 ∙ tc

b)

c) Pentru a calcula bătaia, xb, trebuie să calculăm distanța de la proiecția inițială pe sol (Oʹ) până la punctul de impact cu solul (Oʹʹ) :
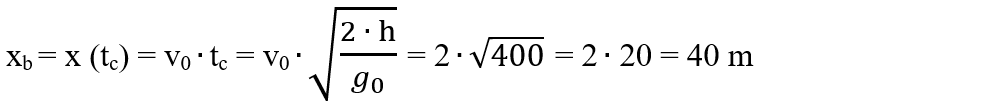
d) Pentru a obține ecuația traiectoriei, din ecuațiile

se elimină timpul:
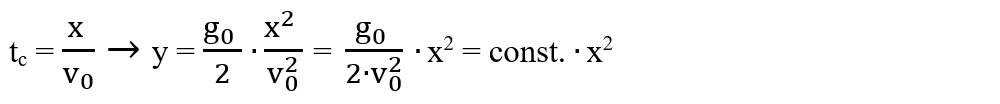
y = const. ∙ x2 este ecuația unei parabole care trece prin originea O a sistemului Oxy.