II.24. Probleme recapitulative rezolvate - Rețele electrice. Efectul curentului electric

🔓 Probleme recapitulative rezolvate - Rețele electrice. Efectul curentului electric. Forța electromagnetică.

1. Determină rezistenţa echivalentă a rezistoarelor din următoarea grupare mixtă:

Rezolvare:

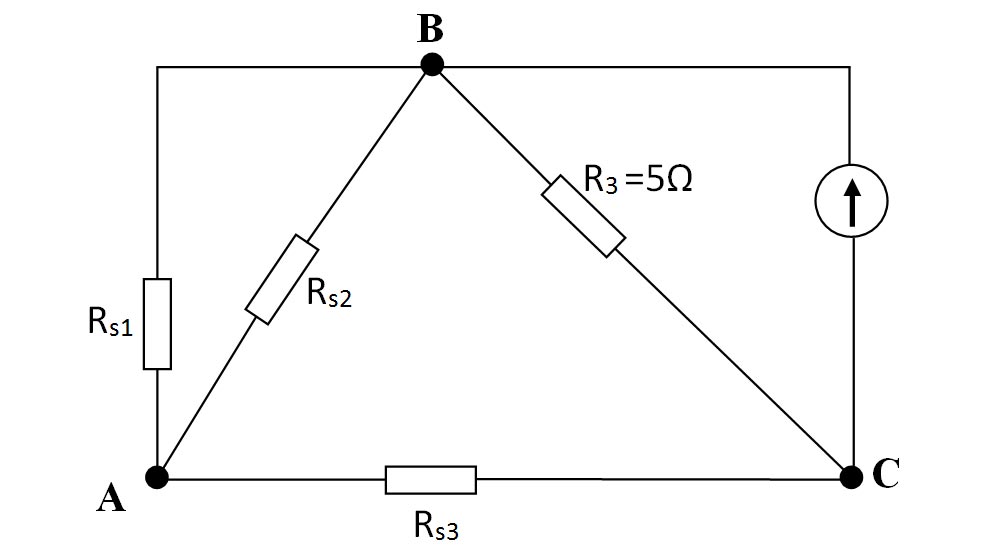
Notăm pe rețea toate nodurile cu litere mari.

Mergem pe conturul circuitului de la un nod la altul și echivalăm grupările de rezistoare cu rezistoare echivalente, serie sau paralel.

Între nodul A și B, în partea stângă, avem 2 rezistoare pe aceeași latură (R₁ și R₂), deci sunt în serie și le echivalăm cu R_s1.

Între nodul A și B avem 2 rezistoare pe aceeași latură (R₄ și R₇), deci sunt în serie și le echivalăm cu R_s2.

Între nodul B și C avem 1 rezistor (R₃), pe care îl copiem.

Între nodul A și C avem 2 rezistoare pe aceeași latură (R₅ și R₆), deci sunt în serie și le echivalăm cu R_s3.

Între nodul B și C avem sursa pe care o copiem.

Calculăm rezistențele echivalente:

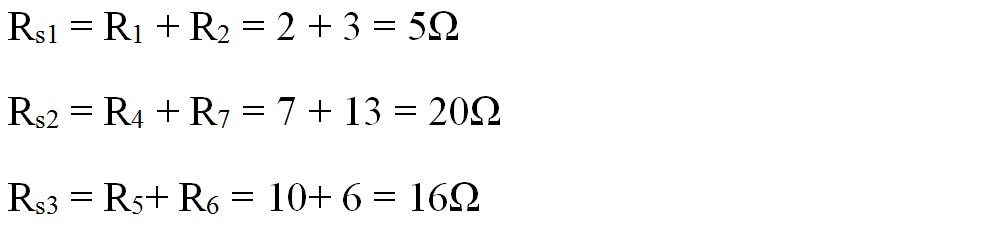
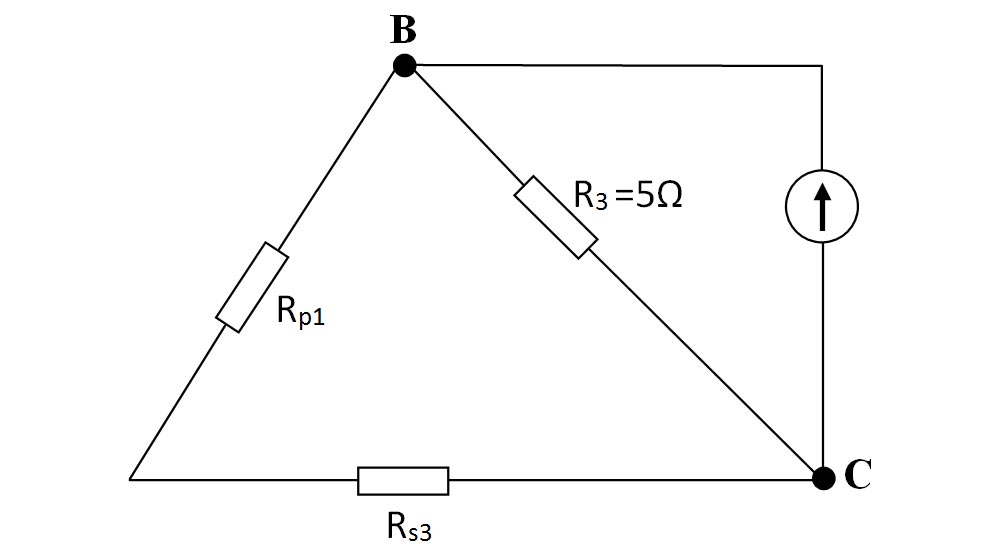
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

Între nodul A și B avem 2 rezistoare (R_s1 și R_s2) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p1.

Restul schemei o copiem.

Calculăm rezistența echivalentă:

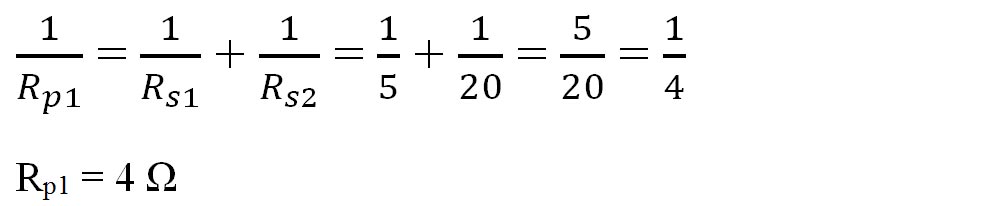
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

Între nodul B și C avem 2 rezistoare (R_p1 și R_s3) pe aceeași latură, deci sunt în serie și le echivalăm cu R_s4.

Calculăm rezistența echivalentă:

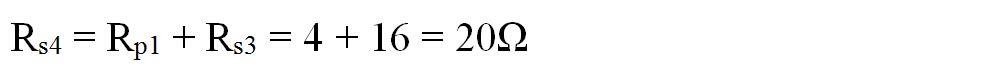
Pe schema nouă, continuăm să echivalăm grupările de rezistoare:

Între nodul B și C avem 2 rezistoare (R_s4 și R₃) pe laturi diferite între aceleași 2 noduri, deci sunt în paralel și le echivalăm cu R_p2.

Calculăm rezistența echivalentă a întregii grupări:

2. Determină intensitățile curenților din următorul circuit ramificat:

Rezolvare:

Notăm cu litere mari nodurile rețelei (A și B).

Notăm laturile rețelei, stabilim arbitrar sensurile curenților de pe fiecare latură:
AE1B (I₁)
AE2B (I₂)
AR3B (I₃)

Notăm ochiurile simple ale rețelei. Stabilim arbitrar (cum dorim) câte un sens de parcurs pentru fiecare ochi (orar sau antiorar).

Aplicăm prima teoremă a lui Kirchhoff: “Suma algebrică a intensităților curenților care intră într-un nod de circuit este egală cu suma intensităților curenților care ies din nodul respectiv“.

Pentru n = nr. noduri, se scriu (n-1) ecuații cu prima teoremă a lui Kirchhoff, aplicată nodurilor de rețea, în cazul nostru pentru un singur nod:
I₁ + I₂ = I₃

Aplicăm a doua teoremă a lui Kirchhoff: “Suma algebrică a tensiunilor electromotoare pentru un ochi de circuit este egală cu suma algebrică a căderilor de tensiune din acel ochi de circuit“, pentru două ochiuri simple:

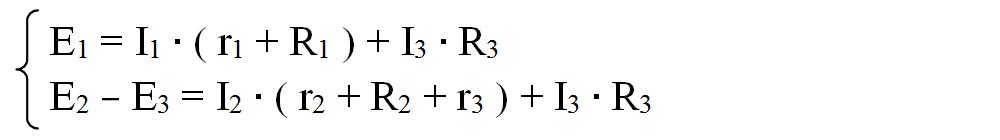
Facem un sistem de 3 ecuații și cu cele trei necunoscute I₁, I₂, I₃.

Înlocuim datele numerice:

Scoatem pe I₁ din prima ecuație:

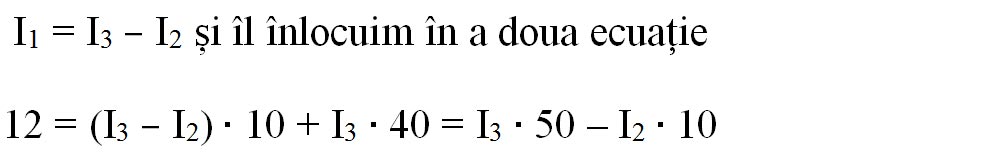
Rezolvăm sistemul cu 2 ecuații și 2 necunoscute, prin reducere:

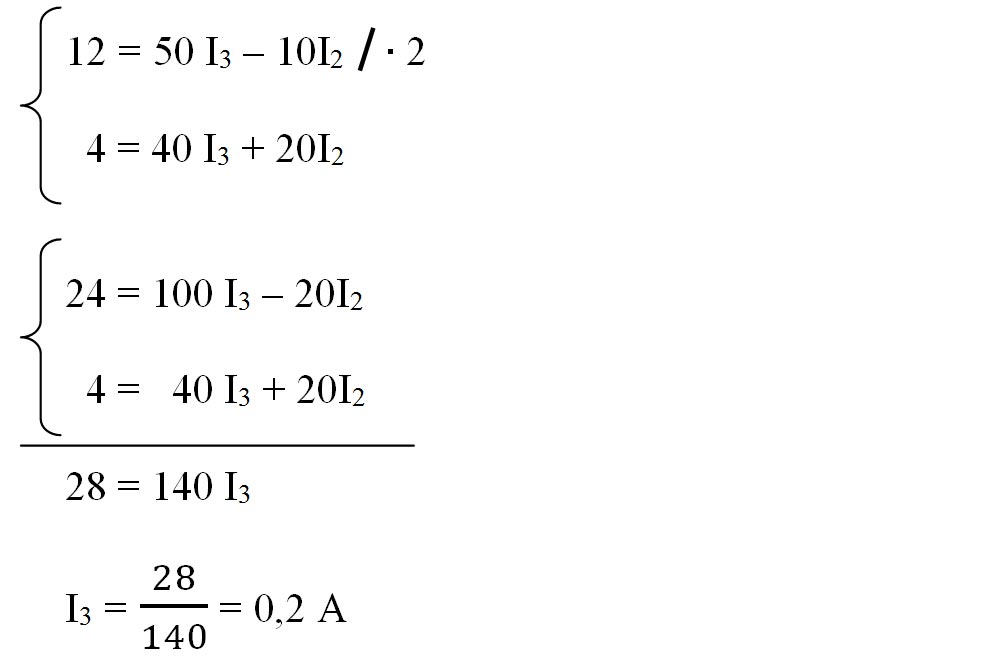
Înlocuim pe I₃ într-o ecuație cu I₂:

Schimbăm sensul curentului I₂ ales inițial, arbitrar, pe rețea:

Din prima ecuație îl aflăm pe I₁:

3. Realizează electroliza fluorurii de zinc (ZnF₂).

4. Rezistența internă a unei baterii crește treptat în timp de când a fost fabricată, chiar dacă nu este folosită, tensiunea electromotoare a acesteia rămânând constantă. Astfel bateria, în timp, chiar dacă nu este folosită, va produce un curent de intensitate mai mică, crescându-i rezistența internă.

Poți determina vârsta unei baterii legând ampermetrul la bornele bateriei și citind intensitatea la scurtcircuit.

Pentru o baterie de 1,5 V, I_sc = 2-3 A, când este nou fabricată.

a) Determină cât este rezistența internă a bateriei când este nouă și la ce valoare ajunge când I_sc = 1,3 A.

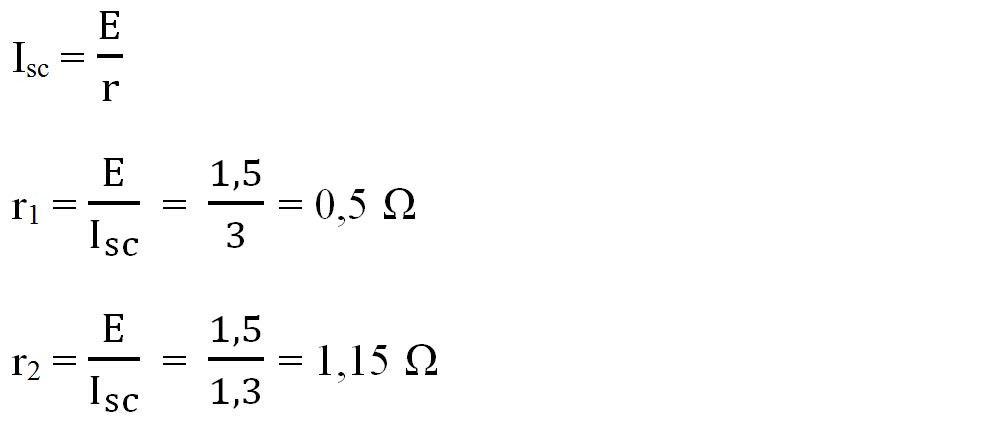
b) Determină cât este rezistența internă a acumulatorului de 12V când este nou, știind că are o intensitate la scurtcircuit I_sc = 40A.

5. O sursă electrică cu t.e.m. de 12 V are o rezistență internă de 0,5 Ω. Ea este legată la un bec cu rezistența de 10 Ω.

Se cere:

a) Cât este intensitatea curentului ce trece prin bec dacă rezistența ampermetrului este de 0,001 Ω (considerăm că nu este un ampermetru ideal care are rezistența zero)?

b) Cât este intensitatea măsurată de ampermetru dacă scoatem becul din circuit ?

c) Cât este intensitatea curentului dacă la bornele becului legăm un voltmetru care nu este ideal, având o rezistență de 100.000 Ω ( voltmetrul ideal are rezistența care tinde spre infinit, pentru a nu permite trecerea curentului prin acesta și astfel se obține citirea corectă) ?

d) Dacă legăm direct voltmetrul la bornele sursei, cât este intensitatea curentului ?

Rezolvare:

Scriem datele problemei:
E = 12 V
r = 0,5 Ω
R_b = 10Ω
R_A = 0,001 Ω
R_V = 100.000 Ω

a)

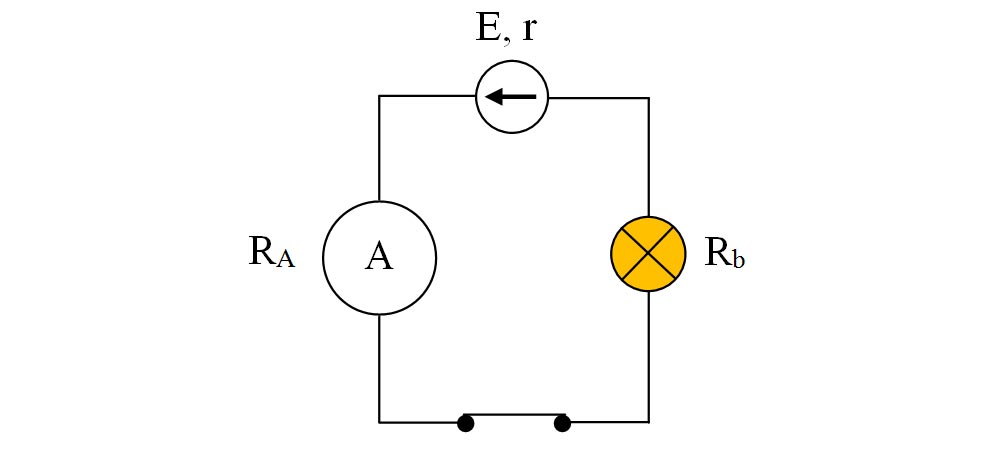
Becul și rezistorul ampermetrului și rezistența sursei sunt în serie și au rezistența echivalentă:

b)

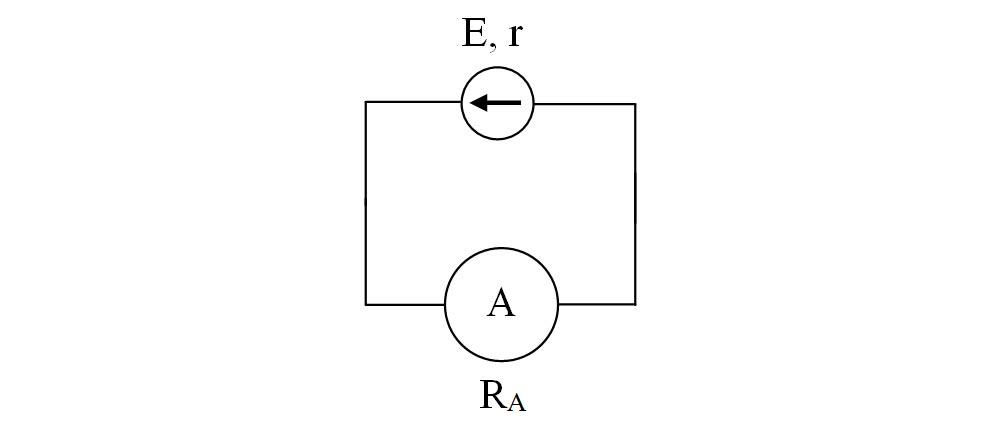
Dacă ampermetrul ar fi fost unul ideal, cu rezistența 0, el ar fi scurtcircuitat sursa și ar fi măsurat curentul de scurtcircuit cu formula

Însă acest ampermetru nu are rezistența 0 și vom avea o intensitate:

c)

R_b și R_V sunt în paralel și le calculăm rezistența echivalentă R_p:

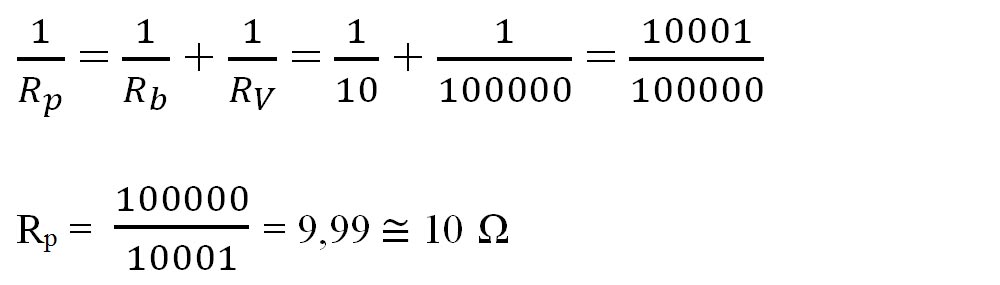
R_p, R_A și r sunt în serie și au rezistența echivalentă:

d)

Legând direct voltmetrul la sursă, r și R_V vor fi în serie și intensitatea va deveni:

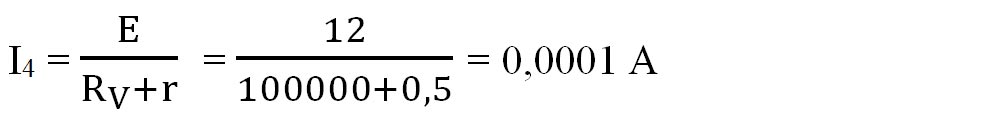
Dacă voltmetru ar fi fost unul ideal (cu rezistența infinită), intensitatea curentului ar fi fost zero.

6. Un resort are lungimea inițială de 10 cm. Când suspendăm de el o tijă de fier cu mase marcate de 20 g, lungimea lui este de 14 cm. Sub tija de fier se așază un electromagnet legat la o baterie, caz în care lungimea resortului ajunge la 18 cm.

Se cere:

a) Greutatea tijei.

b) Forța de atracție a electromagnetului.

Rezolvare:

Scriem datele problemei și le transformăm în SI:
l₀ = 10 cm = 0,1 m
l₁ = 14 cm = 0,14 m
l₂ = 18 cm = 0,18 m
m = 20 g = 0,02 kg

a) Calculăm greutatea tijei cu masa marcată:
G = m ∙ g = 0,02 ∙ 10 = 0,2 N

Forța deformatoare este chiar greutatea tijei și ea produce o deformare de :
Δl₁ = l₁ – l₀ = 0,14 – 0,10 = 0,04 m
F = G = k ∙ Δl₁

b) Calculăm a doua deformare:

Δl₂ = l₂ – l₀ = 0,18 – 0,10 = 0,08 m = 2 ∙ Δl₁

Forța de atracție a electromagnetului asupra tijei de fier adunată cu greutatea tijei produce a doua deformare a resortului:

F_a + G = k ∙ Δl₂

Fa = k ∙ Δl₂ - k ∙ Δl₁ = k ∙ 2Δl₁ - k ∙ Δl₁ = k ∙ Δl₁ = G = 0,2 N

7. Becurile B₂ și B₃ au valorile nominale de 6 V și 0,1 A și funcționează normal. Ampermetrul indică 300 mA. Este identic becul B₁ cu becurile B₂ și B₃ ?

Rezolvare:

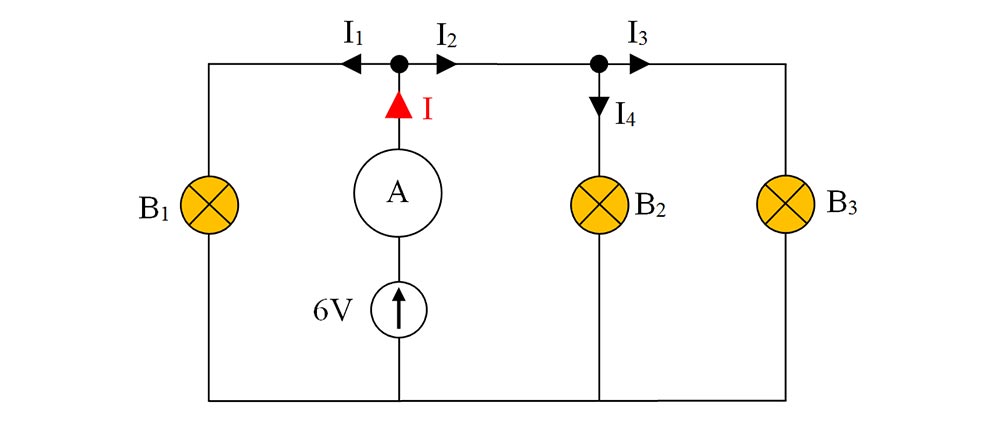
I = I₁ + I₂ = 0,3 A

I₂ = I₃ + I₄ = 0,2 A

I₃ = I₄ = 0,1 A

I₁ = 0,1 A

Curentul din ramura principală cu sursa și cu ampermetrul se ramifică pe laturile becurilor B2 și B3, care fiind identice și legate în paralel, vor avea fiecare un curent de intensitate egală cu jumătate din curentul I₂, adică 0,1 A.

Becul B₁ are tensiunea nominală de 6 V și intensitatea nominală de I₁ = 0,1 A.

Deci becul B₁ este identic cu becurile B₂ și B₃.