II.16.2. Coborârea uniformă a unui corp pe un plan înclinat

📚

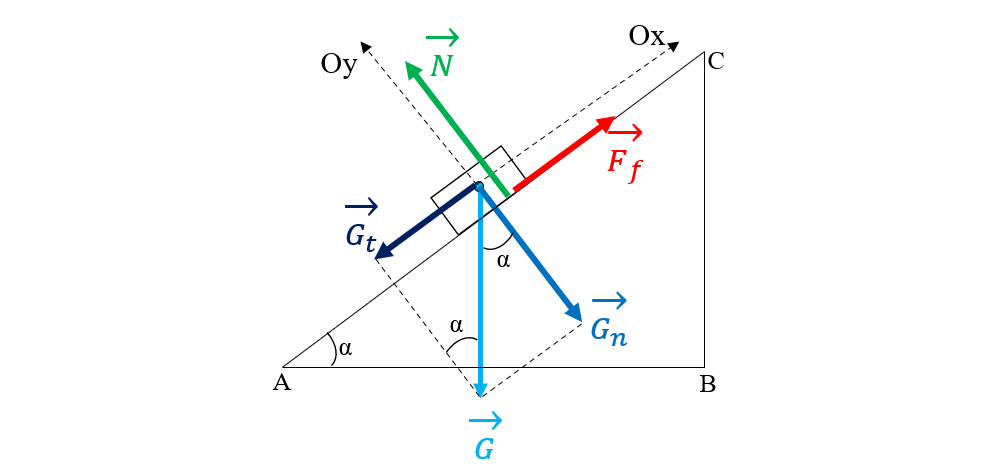
• Desenăm un corp pe un plan înclinat.

• Trasăm greutatea corpului, G, din mijlocul corpului (centru de greutate, notat cu C) pe verticală, în jos.

• Din C trasăm punctat axa O_x, paralelă cu planul înclinat.

• Din C trasăm punctat axa O_y, perpendiculară pe planul înclinat.

• Descompunem greutatea după aceste două axe, astfel încât greutatea corpului se poate înlocui cu perechea de forțe G_t și G_n.

  • Forța G_t se numește componenta tangențială a greutății și acționează pe direcția mișcării O_x (paralelă cu planul înclinat),

  • Forța G_n se numește componenta normală a greutății și acționează perpendicular pe direcția mișcării O_x (perpendiculară pe planul înclinat).

• Trasăm reacțiunea normală, N, de la baza corpului, un segment orientat pe direcția O_y și egal cu G_n.

• Trasăm forța de frecare, F_f, de la baza corpului, un segment orientat pe direcția O_x, în sus și egal cu G_t.

• Greutatea este suma vectorială a acestor două forțe, G_t și G_n.

• Modulele celor trei forțe sunt legate prin relația

conform teoremei lui Pitagora aplicată în triunghiul dreptunghic format de cele trei forțe.

• Planul înclinat este reprezentat printr-un triunghi dreptunghic care este asemenea cu triunghiul dreptunghic format de greutate și componentele sale. Din asemănarea triunghiurilor precizate se găsesc relațiile:

📚

Corpul lăsat liber pe planul înclinat coboară uniform atunci când |F_f| = |G_t| și |N| = |G_n|.

🔓 Problemă rezolvată

1. Pe un derdeluș (plan înclinat) cu înălțimea de 6 m și lungimea de 10 m, un copil cu greutatea de 400 N coboară uniform pe o folie de plastic. Reprezintă grafic forțele ce acționează asupra copilului și determină modulele acestor forțe.

Rezolvare:

Notăm datele problemei:

h = BC = 6 m
l = AC = 10 m
G = 400 N
v = const.
F_f = ?

Calculăm cu teorema lui Pitagora baza planului înclinat, b = AB:

l² = b² + h²

b² = l² – h² = 100 – 36 = 64

b = √64 = 8 m

Desenăm triunghiul planului înclinat și corpul ce coboară uniform pe planul înclinat.

Reprezentăm greutatea corpului și o descompunem după două direcții perpendiculare între ele : Ox paralelă cu planul înclinat și Oy perpendiculară pe planul înclinat.
G = greutatea corpului care se descompune după cele două direcții perpendiculare Ox și Oy în G_t (greutatea tangențială) și G_n (greutatea normală).

Planul înclinat este reprezentat printr-un triunghi dreptunghic care este asemenea cu triunghiul dreptunghic format de greutate și componentele sale. Din asemănarea triunghiurilor precizate se găsesc relațiile aplicând sin α atât în triunghiul forțelor, cât și în triunghiul planului înclinat:

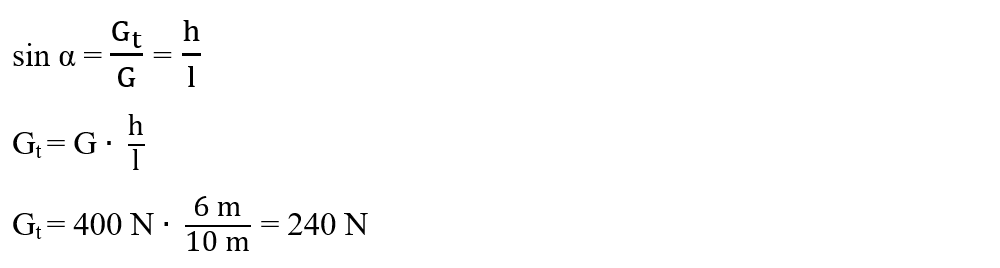
Din asemănarea triunghiurilor precizate se găsesc relațiile aplicând cos α atât în triunghiul forțelor, cât și în triunghiul planului înclinat:

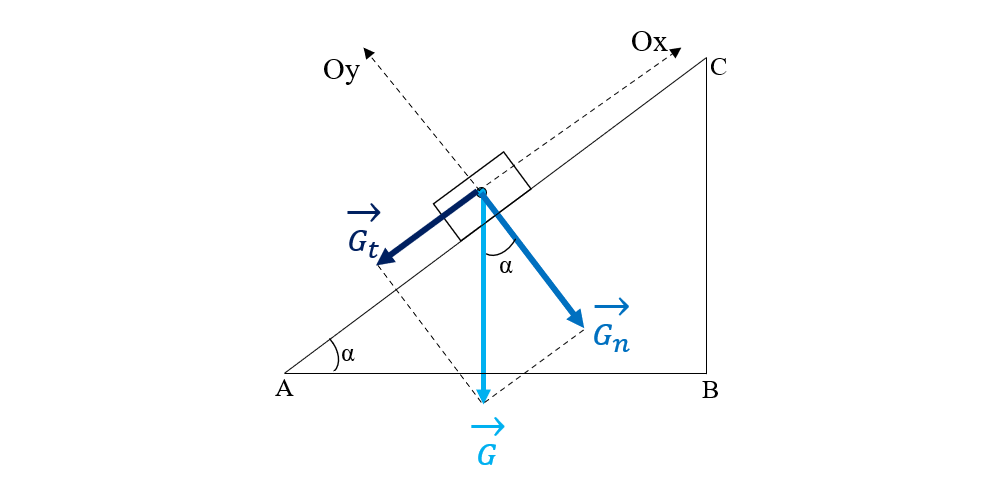
La coborârea uniformă (v = constantă) a unui corp pe un plan înclinat:

Rezultanta forțelor pe direcția Ox este zero deoarece corpul se mișcă uniform (v = const.) pe acestă direcție paralelă cu planul înclinat. Prin urmare, modulul greutății tangențiale este egal cu modulul forței de frecare. Ele sunt egale în modul, dar au sensuri opuse.

R_x = 0 → | G_t | = | F_f |
Deci, | G_t | = | F_f | = 240 N

Rezultanta forțelor pe direcția Oy este zero, deoarece corpul nu se mișcă pe această direcție perpendiculară pe planul înclinat. Prin urmare, modulul greutății normale este egal cu modulul reacțiunii normale (normalei la suprafața planului înclinat).

Ele sunt egale în modul, dar au sensuri opuse.

Ry = 0 → | G_n | = | N |
Deci, | G_n | = | N | = 320 N

Desenăm pe direcția Ox, în sus forța de frecare egală în modul cu greutatea tangențială.

Desenăm pe direcția Oy, în sus reacțiunea normală (normala) egală în modul cu greutatea normală.