II.4. Prisma optică.
II.4.1. Refracția luminii monocromatice în prisma optică.
Prisma este un mediu transparent (cu indicele de refracție n) mărginit de două fețe plane, care fac între ele un unghi diedru, numit unghiul prismei (A).

Când raza incidentă (SI) cade pe fața AB a prismei se refractă (prima rază refractată II'), apropiindu-se de normala NI (naer < nprismă) după legea:
sin i = n ∙ sin r
Raza II' se refractă la căderea pe fața AC a prismei în punctul I', depărtându-se de normala NN' (nprismă > naer), după legea:
n ∙ sin r' = sin i'
Unghiul dintre direcția razei incidente (SI) și direcția razei emergente (I'R) se numește unghi de deviație (δ) care are valoarea:
δ = i + i' – (r + r') = i + i' – A
🔦 Observații matematice
A este unghi exterior în ΔM'II' și δ este unghi exterior în ΔMII'
A + M' =180°
A = 180 - M' = 180 – 180 + (r + r')
M'= 180 - (r + r')
A = 180 - M' = 180 – 180 + (r + r')
A = r + r'
δ = 180 – M
În Δ IMM':
M = 180 – (i-r) – (i' - r') = 180 – i + r - i' + r'
δ = 180 – M = 180 – 180 + i + i' – (r + r') = i + i' – (r + r') = i + i' – A
Pentru a stabili condiția de emergență (adică raza incidentă să iasă din prismă) trebuie să nu aibă loc reflexia totală a razei II' pe fața AC, adică:
r' ≤ l (unghiul limită).
Cum A = r + r' → r' = A – r
r ≥ A – l → sin r ≥ sin (A – l)
Dar din prima lege a refracției avem

Unghiul maxim de incidență este
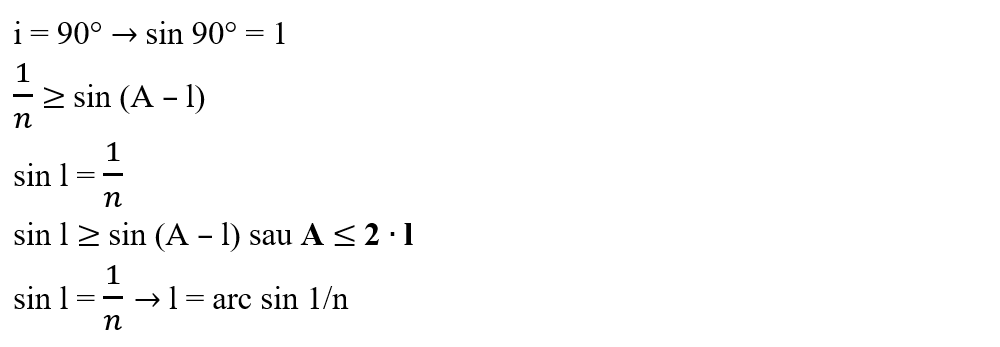
Condiția de emergență:
O rază incidentă pe prismă poate ieși din prismă dacă unghiul ei refringent (A) îndeplinește condiția:
A ≤ 2 ∙ arc sin 1/n
Dacă prisma are A > 2 ∙ arc sin 1/n, toate razele incidente pe prismă se vor reflecta total pe fața AC.
Deviația minimă:
Când unghiul de incidență (i) variază și unghiul de deviație (δ) variază, luând întotdeauna valori mai mari decât o anumită valoare minimă (δm).
Când i = i' și r = r' obținem valoarea unghiul de deviație minimă (δm):
δm = 2 ∙ i – A
Dacă măsurăm experimental unghiul de deviație minimă se poate determina indicele de refracție al prismei cu formula:

🔦 Observație
Relația

ne arată dependența unghiului de deviație minimă (δm) de indicele de refracție al prismei explicând descompunerea luminii albe în culorile curcubeului.
II.4.2. Prisma cu reflexie totală.
🔓 Problemă rezolvată
1. O prismă optică are indicele de refracție √2. Află dacă o rază de lumină ce cade pe o față a prismei sub un unghi i1 = 45° poate suferi reflexie totală pe fața AC a prismei.
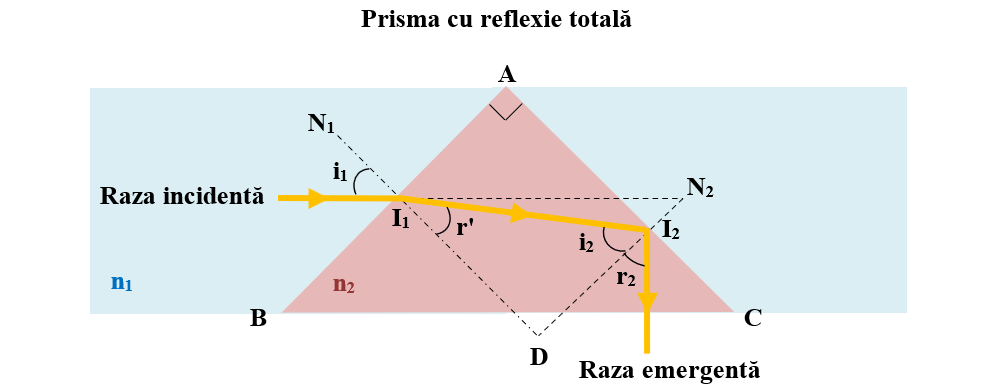
Rezolvare:
- Secțiunea transversală a prismei este un triunghi dreptunghic isoscel cu A = 90° și B = C = 45°.

- În ΔDI1I2: D = r' + i2
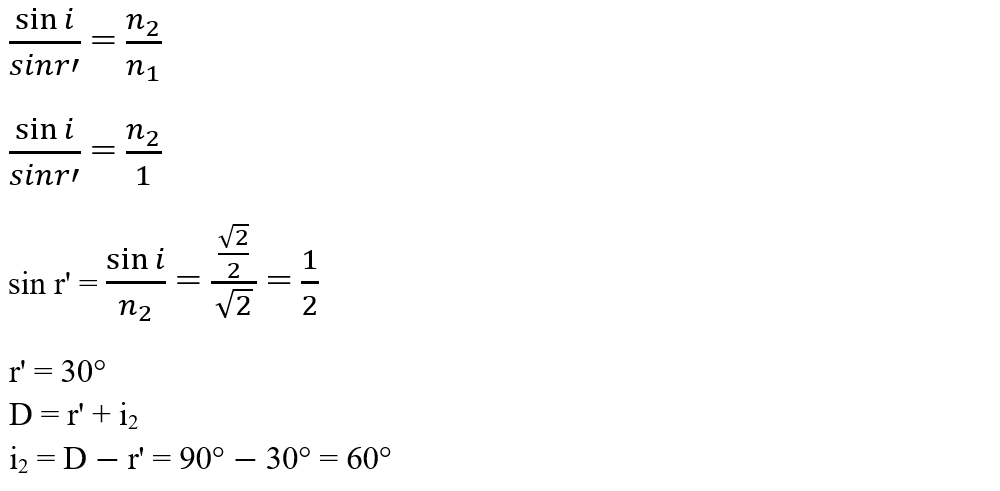
- Pentru a afla unghiul limita aplicăm a II–a lege a refracției punând condiția ca unghiul de incidență să fie egal cu unghiul limită (i2 = l) și unghiul de refracție r' = 90°. Știind că sin 90° = 1 obținem:

- Cum i2 > l și primul mediu (sticla prismei) are indicele de refracție mai mare decât al doilea mediu (aerul) înseamnă că sunt îndeplinite ambele condiții pentru a se produce reflexie totală.