Probleme rezolvate

🔓 Probleme rezolvate - Corp. Mobil. Reper. Sistem de referință. Mișcare și repaus. Traiectorie

3.1. Te afli pe bancheta autobuzului care te duce la școală.

În ce stare mecanică (mișcare sau repaus) ești față de:

a) Șoferul autobuzului? Față de șofer sunt în repaus, deoarece nu îmi schimb poziția (distanța) față de acesta.

b) Banchetă? Față de banchetă sunt în repaus, deoarece nu îmi schimb poziția față de aceasta.

c) Pământ? Față de Pământ sunt în mișcare, deoarece îmi schimb distanța față de acesta.

d) Mașinile care circulă pe șosea? Față de mașini sunt în mișcare, deoarece îmi schimb poziția față de acestea.

3.2. Desenează traiectoriile unui punct de pe roata bicicletei tale față de:

a) axul (centrul) roții.

Traiectoria este circulară (cerc):

b) sol (Pământ).

Traiectoria este curbilinie :

🔓 Problemă rezolvată - Distanța parcursă. Durata mișcării

3.3. Un biciclist pleacă de la kilometrul 20 la ora 12:00 și ajunge la kilometrul 60 la ora 13:30. Ce distanță a parcurs biciclistul și cât a durat mișcarea?

Rezolvare:

Scriem datele problemei:

Poziția inițială : x₁ = 20 km
Poziția finală : x₂ = 60 km
Momentul inițial : t₁ = 12:00
Momentul final : t₂ = 13:30

Aplicăm formula distanței și a duratei mișcării și înlocuim datele problemei:

d = Δx = x₂ – x₁ = 60 km – 20 km = 40 km
Δt = t₂ – t₁ = 13:30 – 12:00 = 1h 30min = 1,5 h

🔓 Probleme rezolvate - Viteza medie. Caracteristicile vitezei (direcție și sens)

3.4. Un mobil pleacă de la borna kilometrică 100 la ora 10:15 și ajunge la borna kilometrică 275 la ora 11:50. Cu ce viteză medie s-a deplasat mobilul în m/s ?

Rezolvare:

Scriem datele problemei:

x₁ = 100 km
t₁ = 10:15
x₂ = 275 km
t₂ = 11:50
v_m = ? m/s

Scriem formula vitezei medii, calculăm distanța parcursă și durata mișcării în SI și înlocuim în formulă:

3.5. Un șofer pleacă de la borna kilometrică 240 la ora 10:50 și ajunge la borna kilometrică 80 la ora 11:40. Cu ce viteză medie a mers șoferul în m/s și în km/h ?

Rezolvare:

Scriem datele problemei:

x₁ = 240 km
t₁ = 10:50
x₂ = 80 km
t₂ = 11:40
v_m = ? m/s, km/h

Scriem formula vitezei medii, calculăm distanța parcursă și durata mișcării în SI și înlocuim în formulă:

Transformăm viteza din m/s în km/h:

3.6. Transformă vitezele următoare în m/s:

Rezolvare:

3.7. Diana locuiește la o distanță D = 2 km față de școală. Într-o zi ea a aplecat de acasă la ora 7:10. După ce parcurge un sfert din distanță, realizează că și-a uitat proiectul la fizică și se întoarce să îl ia. La ora 7:50 ajunge la școală. Să se determine viteza medie a Dianei în m/s și în km/h.

Rezolvare:

Scriem datele problemei:

D = 2 km = 2000 m
t₁ = 7:10
t₂ = 7:50

Dacă poți reține, o viteză exprimată în m/s poate fi transformată în km/h, prin înmulțirea valorii ei cu 3,6.

🔓 Problemă rezolvată - Tipuri de mișcare. Mișcarea rectilinie uniformă

3.8. Antrenorul Luizei a cronometrat mișcarea ei pe pista de 100 m și a trecut datele mișcării în următorul tabel.

a) Ce fel de mișcare are Luiza ?

b) Calculează viteza medie.

c) Determină legea mișcării.

Rezolvare:

a) Observăm în tabel faptul că, Luiza parcurge distanțe egale (25 m) în intervale de timp egale (3 s). Deci Luiza are o mișcare rectilinie și uniformă. Atenție, în cazul în care viteza corpului este constantă, obligatoriu traiectoria este rectilinie. În mișcarea curbilinie și în cea de rotație, viteza nu poate fi constantă.

Când viteza ne dă cu perioadă, este bine să lucrăm cu fracție ireductibilă

c) Înlocuim în legea mișcării pe x₀, v și pe t₀ :

🔓 Probleme rezolvate - Reprezentarea grafică a mișcării

3.9. Pentru a reprezenta graficul mișcării unui mobil (alergării Luizei pe pista de 100m) trebuie să se parcurgă următoarele patru etape:

3.9.A. Se realizează un tabel cu datele mișcării (pozițiile și momentele de timp corespunzătoare acestora).

3.9.B. Se trasează axele, două drepte perpendiculare, una orizontală și una verticală, pe foaie de matematică sau pe hârtie milimetrică. Axa orizontală se numește axa abscisei (Ox) și cea verticală se numește axa ordonatei (Oy). Se gradează (calibrează) cele două axe prin alegerea unui etalon pentru fiecare, astfel încât să putem reprezenta toate pozițiile mobilului și momentele corespunzătoare lor.

Pentru exemplu nostru voi alege ca etalon (scară) pentru axa distanței: 1 cm : 5 m, iar pentru axa timpului: 1 cm : 1 s.

Punctul de intersecție al axelor este O = originea pentru fiecare axă, adică în acest punct avem 0 m și 0 s.
Abscisa este axa timpului. Se notează axa și la extremitatea acesteia, se scrie t (s).
Ordonata este axa distanțelor (pe această axă se notează pozițiile mobilului). Se notează axa și la extremitatea ei se scrie x (m).

3.9.C. Se trasează pe grafic fiecare punct din tabel.

• Primul punct este chiar în origine, O (x₀=0, t₀=0).

• Pentru a reprezenta al doilea punct, A (x₁ = 25 m, t₁ = 3 s), procedăm în felul următor: în dreptul valorii numerice a lui 3 s se duce, punctat, o dreaptă verticală. În dreptul valorii numerice a lui 25 m se duce, punctat, o dreaptă orizontală. Punctul de intersecție al celor două drepte punctate este punctul de pe grafic de coordonate A(x₁, t₁).

• Se continuă și cu celelalte trei puncte: B (x₂, t₂), C (x₃, t₃), D(x₄, t₄), după modelul arătat mai sus, până sunt trecute pe grafic toate cele cinci puncte din tabel.

3.9.D. Se trasează graficul mișcării prin unirea tuturor punctelor construite anterior.

🔦 Observaţie: Nu confunda traiectoria mobilului cu graficul mișcării!

🔦 Observaţii:

Folosind graficul mișcării putem afla mai multe informații referitoare la modul în care se deplasează un mobil:

graficul mișcării rectilinii și uniforme este o dreaptă.
dacă mobilul este în repaus, graficul mișcării este o dreaptă orizontală.
pentru a desena graficul mișcării este suficient să reprezentăm minim două puncte care unite, vor determina dreapta graficului.
dreapta care reprezintă mișcarea rectilinie și uniformă este mai înclinată (formează un unghi mai mare cu orizontala) atunci când viteza este mai mare.

3.10. Graficul mișcării unui mobil este reprezentat în figura următoare:

a) Care sunt pozițiile mobilului la momentele: t₁ = 0, respectiv t₂ = 2h?

b) Se depărtează sau se apropie mobilul de reper?

c) În ce moment ajunge mobilul la poziția de 120 km?

d) În ce moment ajunge mobilul în reper?

e) Care este viteza mobilului în m/s?

Rezolvare:

a) La t₁ = 0 h, mobilul este în poziția x₁ = 200 km. Din origine, urcăm pe verticală (axa poziției) până intersectăm graficul și așa determinăm poziția x₁ = 200 km. La t₂ = 2 h, mobilul este în poziția x₂ = 100 km. Urcăm pe verticală (axa poziției) până intersectăm graficul și de la grafic mergem pe orizontală punctat, până intersectăm axa poziției, așa determinăm poziția x₂ = 100 km.

b) Mobilul se apropie de reper (poziția 0 km), deoarece pozițiile mobilului scad odată cu creșterea timpului .

c) La 120 km, mobilul este la momentul de 1,5 h de la plecare. Pornim cu o dreaptă punctată din 120 km pe orizontală, până întâlnim graficul și de aici, coborâm punctat pe verticală pe axa timpului.

d) În reper, poziția 0 km, avem timpul de 4 h. Din origine, mergem pe orizontală (axa timpului) până intersectăm graficul și așa determinăm timpul de 4 h.

e) Scriem formula vitezei:

La calculul distanței, scădem x₁ - x₂, deoarece x₁ > x₂ (distanța este tot timpul pozitivă).

La calculul timpului, scădem t₂ - t₁, deoarece t₂ > t₁ (timpul este pozitiv).

3.11. În următorul tabel sunt trecute datele mișcării unui mobil.

Reprezintă graficul mișcării folosind ca etaloane

1 cm : 2 s
1 cm : 2 m.

Rezolvare:

3.12. În următorul tabel se dau datele mișcării a două mobile M₁ și M₂.

a) Determină pozițiile mobilului M₂ știind legea de mișcare x_M2 = 30 + 12∙ t

b) Realizează graficele mișcării celor două mobile.

Etaloane:

1 cm : 30 m

1 cm : 5 s

c) Care este poziția celor două mobile la t = 20 s ?

d) Determină viteza medie a celor două mobile.

e) Scrie legea de mișcare pentru mobilul M₁.

Rezolvare:

a) x_M2 = 30 + 12 ∙ t

x_0M2 = 30 + 12 ∙ 0 = 30 m

x_1M2 = 30 + 12 ∙ 5 = 90 m

x_2M2 = 30 + 12 ∙ 30 = 390 m

x_3M2 = 30 + 12 ∙ 40 = 510 m

b) Graficul de mișcare al celor două mobile:

c) Pentru M₁: la t = 20 s avem poziția x = 120 m.

Pentru M₂: la t = 20 s avem poziția x = 270 m.

e) x_M1 = x₀ + v(t – t₀) = 0 + 6 ∙ t = 6t

🔓 Probleme rezolvate - Mișcarea rectilinie uniform variată

3.13. Privește cu atenție datele despre mișcarea fetei. Cum determinăm tipul mișcării ei ?

Observăm că în intervale de timp egale (de 4 s), fata parcurge distanțe din ce în ce mai mari. Dacă efectuăm calculul vitezelor pe fiecare porțiune, acestea cresc. Vitezele cresc cu valori egale (Δv = 1 m/s) în intervale de timp egale (Δt = 4 s). Cum accelerația este raportul dintre variația vitezei pe intervalul de timp, rezultă că mișcarea este rectilinie uniform accelerată.

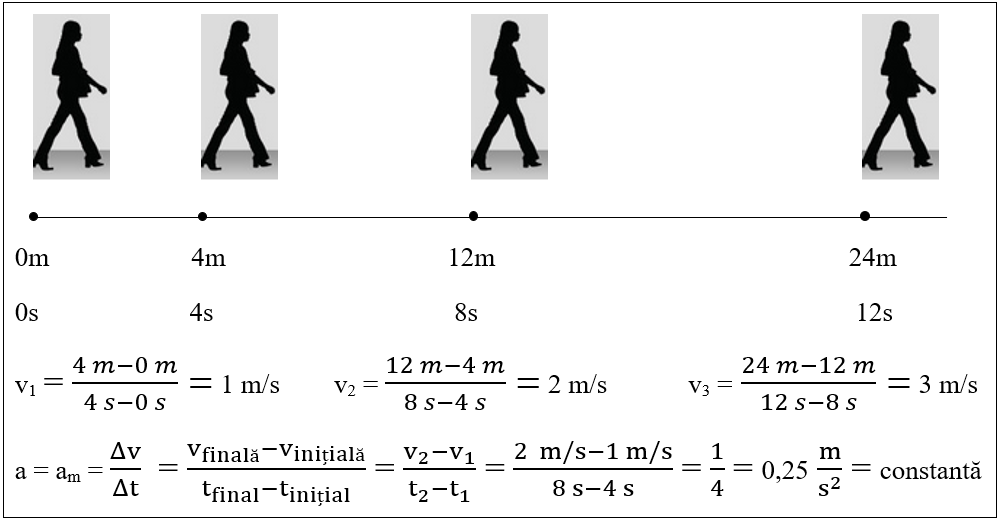
3.14. Pentru a intra într-o depășire, o mașină care se deplasează cu o viteză de 54 km/h, accelerează cu 4 m/s². La ce viteză ajunge mașina după 5 s ?

Rezolvare:

Notăm datele problemei și le transformăm în SI:

Scriem formula accelerației și scoatem necunoscuta, v₂:

🔓 Problemă rezolvată - Masa, măsură a inerţiei. Unităţi de măsură

3.15. O minge de tenis de câmp și una de baschet se deplasează cu aceeași viteză. Pe care o oprești mai ușor?

Rezolvare:

Oprim mai ușor mingea de tenis deoarece, ea are masa mai mică decât cea de baschet. Având masa mai mică are și inerția mai mică și se opune mai puțin la schimbarea stării de mișcare în care se afla.

🔓 Probleme experimentale - Densitatea corpurilor, unitate de măsură. Determinarea densității

3.16. Densitatea, o constantă de material.

Materiale necesare: cântar, 2 pahare Berzelius, cilindru gradat, apă.

Descrierea experimentului:

Măsoară cu cilindrul gradat un anumit volum de apă: V₁ = 50cm³.
Măsoară cu cântarul masa acestui volum de apă: m₁ = 50 g.
Măsoară cu cilindrul gradat un alt volum de apă: V₂ = 200 cm³.
Măsoară cu cântarul masa celui de-al doilea volum de apă: m₂ = 200,1 g.
Calculează pentru fiecare volum de apă, raportul dintre masa și volumul apei.

Ce observi ?

Observaţie: Observăm că deși masa și volumul apei din pahar se modifică, raportul lor rămâne constant.

Concluzia experimentului:

3.17. Determinarea densității unui corp.

Materiale necesare: cântar, un corp (cilindru metalic), cilindru gradat cu apă.

Descrierea experimentului:

Măsoară cu cântarul masa corpului: m = 73,3 g.
Măsoară cu cilindrul gradat volumul corpului: V = 10 cm³.
Calculează raportul dintre masa și volumul corpului.

Observaţie: Raportul dintre masa și volumul corpului reprezintă densitatea corpului.

Concluzia experimentului:

🔓 Problemă rezolvată - Densitatea corpurilor, unitate de măsură. Determinarea densității

3.18. Cât cântărește un litru de ulei alimentar? Densitatea uleiului este de 0,8 g/mL.

Rezolvare:

Notăm datele problemei și le transformăm în SI:

Scriem formula densității și scoatem necunoscuta:

🔓 Problemă experimentală - Greutatea (G)

3.19. Cum măsurăm accelerația gravitațională a Pământului ?

Materiale necesare: dinamometru, corp cu cârlig și discuri crestate.

Descrierea experimentului:

Măsoară cu un dinamometru greutățile mai multor corpuri a căror masă o cunoști.
Calculează pentru fiecare corp raportul G/m. Trece datele în următorul tabel:

Observaţie: Raportul G/m are aceeași valoare pentru fiecare corp în parte. Se obține valoarea 10 N/kg.

Concluzia experimentului:

Raportul G/m are aceeași valoare respectiv 10 N/kg.

🔓 Problemă rezolvată - Greutatea (G)

3.20. Cât cântărește un corp cu o greutate de 1 N ?

Rezolvare:

Notăm datele problemei:
G = 1 N
g = 9,8 N/kg
m = ?

Scriem formula greutății și scoatem necunoscuta :

🔓 Problemă experimentală - Forța elastică (Fe)

3.21. Cum se determină constanta elastică?

Materiale necesare: dinamometru, disc cu mase marcate, riglă.

Observaţie: Greutatea corpului suspendat este forța deformatoare, egală în modul cu forța elastică (au aceeași valoare numerică) : |G₁ | = |F₁ | = |F_e1 |.

Descrierea experimentului:

Suspendă dinamometrul pe un suport.
Măsoară lungimea inițială a resortului dinamometrului: L₀ = 2 cm.
Suspendă de cârligul dinamometrului un corp și măsoară-i greutatea G₁ = F_e1 = 0,12 N.
Măsoară lungimea resortului dinamometrului deformat: L₁ = 3,2 cm.
Calculează alungirea (deformarea) resortului : ΔL₁ = L₁ - L₀ = 1,2 cm.
Mai repetă aceleași operații pentru încă cel puțin un corp de masă diferită față de primul. Trece datele experimentale în următorul tabel :

Observaţie: Raportul F_e / ΔL este constant pentru un resort dat.

Concluzia experimentului:

Cu cât greutatea corpului suspendat crește, cu atât crește și alungirea resortului. Deci, forța elastică este direct proporțională cu deformarea resortului.

🔓 Probleme rezolvate - Forța elastică (Fe)

3.22. Un resort are lungimea inițială de 6 cm și când este deformat are 10 cm. Știind că resortul are 40 N /m, determină:

a) Forța deformatoare.

b) Forța elastică.

c) Ce fel de deformare elastică suferă resortul ?

d) Reprezintă cele două forțe ce acționează asupra resortului.

Rezolvare:

Notăm datele problemei și le transformăm în SI:

a) Scriem legea deformării elastice: |F| = |F_e| = k ∙ ΔL

b) Forța elastică (Fe) este egală în modul cu forța deformatoare (F).

|F_e| = |F| = 1,6 N.

c) Resortul este alungit, deoarece lungimea lui creşte când este deformat.

d) Forța deformatoare (F) o desenăm un segment cu săgeată orientat spre dreapta, deoarece ea alungeşte resortul.

Forța elastică (F_e) o desenăm un segment cu săgeată orientat în sens opus forței deformatoare (spre stânga), deoarece ea readuce la forma inițială resortul.

3.23. Un resort are lungimea inițială de 8 cm, iar deformat are lungimea de 3 cm. Știind forța elastică de 400 N, se cere :

a) Constanta elastică a resortului.

b) Tipul deformării.

c) Reprezentarea forței deformatoare și a forței elastice folosind ca etalon

1 cm = 200 N.

Rezolvare:

Scriem datele problemei:

l₁ = 8 cm

l₂ = 3 cm

F_e = 400 N

a) Scriem legea deformării elastice, calculăm deformarea Δl și scoatem necunoscuta k:

b) Tipul deformării: comprimare, deoarece l₂ < l₁.

c) 1 cm : 200 N

400 : 200 = 2cm au segmentele celor două forțe, egale în modul dar de sens opus.

3.24. Un resort este deformat cu 5 dm de o forță de 3000 N.

a) Cât este forța care deformează același resort cu 900 mm ?

b) Reprezintă graficul deformării în funcție de forța deformatoare, folosind ca etaloane:

pentru axa forței 1cm = 1000 N și
pentru axa deformării 1cm = 0,1 m.

Rezolvare:

Scriem datele problemei și le transformăm în SI:

a) Scriem legea deformării elastice pentru prima forță deformatoare și scoatem necunoscuta k:

Scriem legea deformării elastice pentru a doua forță deformatoare și scoatem necunoscuta F₂:

🔓 Probleme recapitulative rezolvate de dificultate crescută (pentru olimpici) - Mișcare și Repaus

3.25. Un mobil se mișcă uniform încetinit până la oprire cu accelerația de 1,5 m/s², într-un minut. Ce distanță a parcurs mobilul?

Rezolvare:

Notăm datele problemei:
- a = 1,5 m/s² = constantă
- v₀ > 0
- v = 0 (mobilul se oprește)
- Δt = 1 min = 60 s
Scriem formula accelerației și calculăm viteza inițială, v₀, a mobilului:

Din expresia vitezei medii obținem :

Cum în mișcarea uniform variată viteza este o funcție liniară de timp (adică crește/scade constant în aceleași interval de timp), viteza medie este media aritmetică a vitezelor inițială (v₀) și finală (v), obținem:

3.26. Determinarea legii mișcării uniform variată.

Rezolvare:

Din expresia vitezei medii obținem:

Cum în mișcarea uniform variată viteza este o funcție liniară de timp (adică crește/scade constant în aceleași interval de timp), viteza medie este media aritmetică a vitezelor inițială (v₀) și finală (v), obținem:

Din formula accelerației scoatem viteza și apoi o înlocuim în formula poziției:

3.27. O mașină se deplasează cu o viteză constantă de 25 m/s. Un motociclist demarează (pornește) în momentul în care mașina a trecut pe lângă el, cu o mișcare uniform acccelerată, atingând viteza de 25 m/s în 10 s fără a înceta să accelereze. Să se determine timpul după care motociclistul ajunge din urmă mașina.

Rezolvare:

Notăm datele problemei cele referitoare la mașină cu indice 1 și cele referitoare la motociclist cu indice 2:
- v₁ = 25 m/s = constant
- v₂ = 25 m/s = crește constant în intervale de timp egale
- a₁ = 0 m/s²
- a₂ = constant
- Δt₂ = 10 s
- Pentru cele 2 mobile avem x₀, v₀, t₀ = 0, Δt = t
Scriem legea mișcării mobilului 1 (mașinii):

Calculăm accelerația mobilului 2 (motocicletei) și îi scriem legea mișcării:

Punem condiția ca cele două mobile să se întâlnească: x₁ = x₂ și aflăm timpul de întâlnire:

🔓 Probleme recapitulative rezolvate - Inerție. Masă. Densitate. Tipuri de forțe

3.28 O bilă de sticlă de 10 g are densitatea 2,5 g/cm³.

Se cere:

a) Greutatea bilei.

b) Volumul bilei în SI.

Rezolvare:

Scriem datele problemei și le transformăm în SI:

a) Scriem formula greutății și înlocuim datele problemei:

G = masă ∙ accelerație gravitațională = m ∙ g = 0,01 kg ∙ 10 n/kg = 0,1 N

b) Scriem formula densității și scoatem necunoscuta, volumul:

3.29. Uleiul dintr-o olivieră are greutatea de 10 N și densitatea 0,8 kg/L.

Se cere:

a) Masa de ulei.

b) Încape acest ulei din olivieră într-o sticlă de 1 L ?

c) Volumul uleiului în SI.

Scriem datele problemei:

G = 10 N

ρ = 0,8 kg/L

Rezolvare:

a) Scriem formula greutății și scoatem necunoscuta, m:

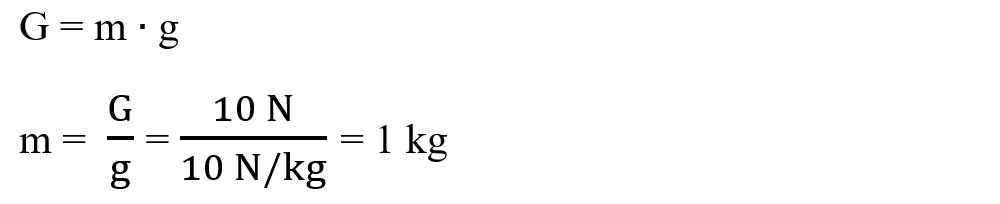
b) Scriem formula densității și scoatem necunoscuta, volumul, V în litri :

Deci, volumul de 1,2 L de ulei din olivieră nu încape într-o sticlă de 1 L (este prea mare și se revarsă).

3.30. Să se transforme următoarele densități în SI:

Rezolvare:

3.31. Ștefania are trei lichide în cantități egale, pe care le-a turnat cu grijă într-un pahar astfel încât să nu se amestece și să formeze trei straturi distincte. Pentru a afla ordinea de turnare a celor trei lichide a studiat tabelul cu densități (la temperatura camerei) și a aflat densitățile celor trei lichide:

Ulei de măsline: 0,91 g/cm³
Glicerină: 1,26 g/cm³
Apă: 1 g/cm³

Se cere:

Care este ordinea în care Ștefania a turnat cele trei lichide în pahar pentru a se forma trei straturi separate? Explică această ordine.

Rezolvare:

Ordinea turnării celor 3 lichide în pahar este următoarea:

I. Glicerina - cu densitatea cea mai mare.

II. Apa - cu densitatea mai mică decât a glicerinei

III. Uleiul de măsline - cu cea mai mică densitate.

3.32. Pe talerele unei balanțe, Marius a pus câte un cub cu latură de 1 cm, astfel: pe cel din stânga a pus un cub din lemn de stejar cu densitatea de 0,7 g/cm³, iar pe cel din dreapta a pus un cub de oțel cu densitatea de 7,7 g/cm³.

Se cere:

a) În ce partea se mișcă acul indicator?

b) Ce masă marcată și pe care taler trebuie adăugată pentru a echilibra balanța?

c) Dacă ambele cuburi au latura de 2 cm, ce masă marcată trebuie adăugată?

Rezolvare:

a) Acul indicator se mișcă în partea stângă, deoarece la același volum, cubul cu densitate mai mare are și masa mai mare.

b) Pentru a afla ce masă marcată trebuie adăugată aflăm masele celor două cuburi și apoi diferența lor:

Masa oțelului este cu 7 g mai mare decât masa lemnului.

Deci trebuie adăugată o masă marcată de 7 g pe talerul din stânga (al lemnului) pentru a echilibra balanța.

c) Pentru a afla ce masă marcată trebuie adăugată aflăm masele celor două cuburi și apoi diferența lor:

Masa oțelului este cu 56 g mai mare decât masa lemnului, când latura cubului este de 2 cm.

Deci trebuie adăugată o masă marcată de 56 g pe talerul din stânga (al lemnului) pentru a echilibra balanța.