III.9. Probleme recapitulative rezolvate - Inerție. Masă. Densitate. Tipuri de forțe
1. O bilă de sticlă de 10 g are densitatea 2,5 g/cm3.
Se cere:
a) Greutatea bilei.
b) Volumul bilei în SI.
Rezolvare:
Scriem datele problemei și le transformăm în SI:

a) Scriem formula greutății și înlocuim datele problemei:
G = masă ∙ accelerație gravitațională = m ∙ g = 0,01 kg ∙ 10 N/kg = 0,1 N
b) Scriem formula densității și scoatem necunoscuta, volumul:

2. Uleiul dintr-o olivieră are greutatea de 10 N și densitatea 0,8 kg/L.
Se cere:
a) Masa de ulei.
b) Încape acest ulei din olivieră într-o sticlă de 1 L ?
c) Volumul uleiului în SI.
Rezolvare:
Scriem datele problemei:
G = 10 N
ρ = 0,8 kg/L
a) Scriem formula greutății și scoatem necunoscuta, m:
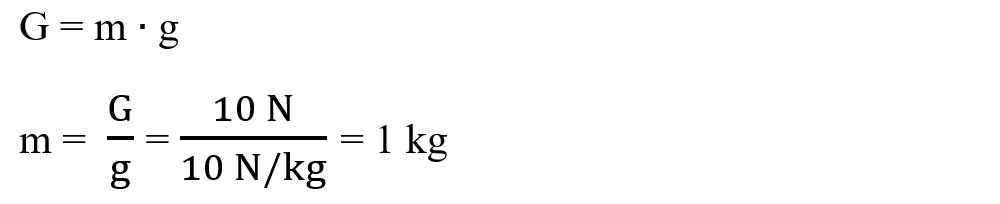
b) Scriem formula densității și scoatem necunoscuta, volumul, V în litri :

Deci, volumul de 1,2 L de ulei din olivieră nu încape într-o sticlă de 1 L (este prea mare și se revarsă).

3. Să se transforme următoarele densități în SI:

Rezolvare:

4. Ștefania are trei lichide în cantități egale, pe care le-a turnat cu grijă într-un pahar astfel încât să nu se amestece și să formeze trei straturi distincte. Pentru a afla ordinea de turnare a celor trei lichide a studiat tabelul cu densități (la temperatura camerei) și a aflat densitățile celor trei lichide:
-
Ulei de măsline: 0,91 g/cm3
-
Glicerină: 1,26 g/cm3
-
Apă: 1 g/cm3
Se cere:
Care este ordinea în care Ștefania a turnat cele trei lichide în pahar pentru a se forma trei straturi separate? Explică această ordine.
Rezolvare:
Ordinea turnării celor 3 lichide în pahar este următoarea:
I. Glicerina - cu densitatea cea mai mare.
II. Apa - cu densitatea mai mică decât a glicerinei
III. Uleiul de măsline - cu cea mai mică densitate.
5. Pe talerele unei balanțe, Marius a pus câte un cub cu latură de 1 cm, astfel: pe cel din stânga a pus un cub din lemn de stejar cu densitatea de 0,7 g/cm3, iar pe cel din dreapta a pus un cub de oțel cu densitatea de 7,7 g/cm3.
Se cere:
a) În ce partea se mișcă acul indicator?
b) Ce masă marcată și pe care taler trebuie adăugată pentru a echilibra balanța?
c) Dar dacă ambele cuburi au fiecare latura de 2 cm, ce masă marcată trebuie adăugată?

Rezolvare:
a) Acul indicator se mișcă în partea stângă, deoarece la același volum, cubul cu densitate mai mare are și masa mai mare.
b) Pentru a afla ce masă marcată trebuie adăugată aflăm masele celor două cuburi și apoi diferența lor:

Masa oțelului este cu 7 g mai mare decât masa lemnului.
Deci trebuie adăugată o masă marcată de 7 g pe talerul din stânga (al lemnului) pentru a echilibra balanța.
c) Pentru a afla ce masă marcată trebuie adăugată aflăm masele celor două cuburi și apoi diferența lor:

Masa oțelului este cu 56 g mai mare decât masa lemnului, când latura cubului este de 2 cm.
Deci trebuie adăugată o masă marcată de 56 g pe talerul din stânga (al lemnului) pentru a echilibra balanța.