V.7.6. Particulele virtuale.
Universul este plin cu particule subatomice şi antiparticule care apar pentru timpi extrem de mici și apoi dispar rin anihilare. Timpul de viață a particulelor este invers proporțional cu masa lor, adică particulele cu mase mai mari au un timp de viață mai scurt.
Masa (m) şi energia (E) particulelor sunt interschimbabile, conform relației lui Einstein:
E = m ∙ c2, unde c este viteza luminii în vid = 3 ∙ 108 m/s.
În mecanica clasică, fenomenele suferite de diferite sisteme de corpuri sunt previzibile, adică pot fi anticipate înainte de a avea loc, calculate și testate.
În mecanica cuantică, procesele sunt imprevizibile, adică orice se poate întâmpla și oricând. Pentru studierea proceselor în care sunt implicate particule de dimensiuni foarte mici se aplică metoda lui Feynman, care calculează probabilitățile de tranziție a unui sistem. Astfel, se imaginează toate posibilitățile de trecere a unui sistem dintr-o stare în alta adunând amplitudinile de probabilitate ale tuturor acestor procese ca niște unde, ținând cont de fază.
Conform principiul de incertitudine al lui Heisenberg nu putem măsura poziția şi impulsul unei particule decât în limita unui anumit grad de incertitudine combinat.

🔦 Observație
Produsul incertitudinilor, de ordinul 10-34 J ∙ s, este atât de mic încât principiul incertitudinii are efect neglijabil la scară macroscopică, în ciuda importanței pe care o are la nivel atomic sau subatomic.
Același principiu se aplică și energiei: pentru a cunoaște cu certitudine energia E a unui sistem avem nevoie de o incertitudine nulă (ΔE = 0) și ar trebui să așteptăm un timp infinit (Δt = ∞). Din acest motiv acest rezultat se numește principiul de incertitudine exprimat în energie-timp.

Diagramele lui Feynman țin cont de toate procesele, atât de cele clasice în care se conservă energia totală a sistemului, cât și de cele care nu respectă conservarea energiei.
Procesele virtuale în care apar particulele virtuale sunt procesele care:
- au un timp de viață foarte scurt, în așa fel încât să nu fie observate direct,
- au loc simultan,
- încalcă legea conservării energiei totale, astfel încât energia totală a sistemului o să varieze cu o valoare ΔE
pentru un timp Δt < h/ΔE (dat de principiul de incertitudine energie-timp).
În timpul reacției, particulele inițiale participă la mai multe procese cuantice (virtuale) care au loc în același timp.
Particulele care intră într-o reacție (de exemplu, coliziunea unui proton cu electroni accelerați) și cele care
rezultă sunt considerate particule reale în reprezentarea energie-impuls, deoarece respectă relația lui Einstein
E2 = m2 ∙ c4 + p2 ∙ c2
E-energia particulei
m-masa de repaus a particulei
c-viteza luminii în vid
p-impulsul particulei).
Particulele intermediare care nu mai satisfac obligatoriu relația lui Einstein E2 = m2 ∙ c4 + p2 ∙ c2, chiar dacă au o energie și un impuls bine definite, se numesc particule virtuale.
Apariția spontană a particulelor virtuale fără o sursă de energie încălcă temporar legea conservării masei-energiei,
care spune că raportul dintre energie și masă este constant:
E/m = c2.
Datorită incertitudinii în măsurarea energiei pentru un timp extrem de mic, acest lucru este permis teoretic, deoarece particulele virtuale apărute în aceste procese se anihilează reciproc într-un termen determinat de principiul incertitudinii, astfel încât să nu fie direct observabile. După ce particulele dispar, se restabilește legea conservării. Crearea perechilor de particule virtuale necesită un câmp cuantic, adică o energie. Deși particulele nu sunt direct detectabile, efectele cumulative ale acestor particule virtuale sunt măsurabile în acceleratoarele de particule.
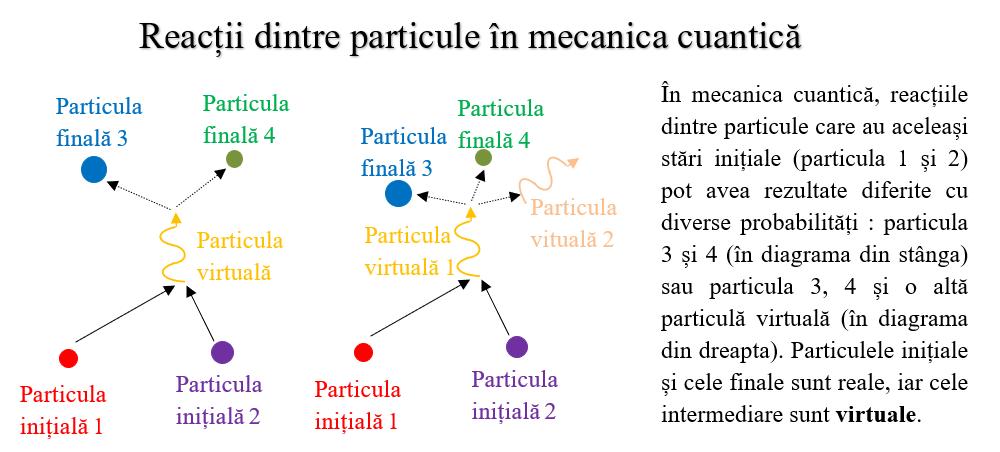
Interacțiunea dintre particule este văzută ca multiple probabilități date de diagramele Feynman a unor rezultate diferite pentru același proces inițial.
Diagrama Feynman este o reprezentare a energiei și impulsului particulelor inițiale, a celor intermediare (virtuale) și a celor finale dintr-o reacție. Această reprezentare arată care sunt stările succesive de energie și impuls în timpul tranzițiilor. Amplitudinea de probabilitate a unui singur proces este dată de produsul amplitudinilor de probabilitate ale proceselor prin care particulele sar de pe niște niveluri de energie și impuls bine definite pe altele. Apoi se adună toate amplitudinile de probabilitate ale tuturor proceselor care conduc la acel rezultat, considerând că sistemul parcurge toate procesele virtuale în același timp.
🔦 Observație
Particulele virtuale există numai pentru un timp finit, permis de principiul de incertitudine energie-timp. Numai procesele virtuale pentru care energia se schimbă pentru un interval scurt de timp, în așa fel încât să nu le putem observa, au o contribuție semnificativă la rezultatul final. Există și procese virtuale în care particulele virtuale au un timp de viață mai lung decât cel permis de principiul de incertitudine energie-timp, dar acestea nu contribuie la rezultatul final.
În fizica cuantică, o fluctuație cuantică (fluctuația vidului) este o schimbare temporară aleatorie a cantității de energie într-un punct din spațiu. Aceste mici fluctuații aleatori ale valorilor câmpurilor reprezintă perechi particulă-antiparticulă virtuale :
- fotonii care mijlocesc interacțiunea electromagnetică;
- bosonii W și Z care mediază interacțiunea slabă;
- gluoni care intermediază interacțiunea tare.

🔦 Observație
Deoarece fotonul virtual are masa de repaus nulă, el poate avea o energie foarte mică ΔE → 0. În acest caz, timpul de viață al fotonului virtual poate fi foarte mare Δt ≈ h/ΔE → ∞, aproape infinit. Datorită timpului de viață foarte mare al fotonului virtual, interacțiunea electromagnetică se manifestă pe distanțe foarte mari (raza de acțiune este infinită).

🔦 Observație
Mezonii sunt particule virtuale care mediază interacțiunea dintre protoni, având o masă nenulă.
Energia minimă de care are nevoie protonul ca să emită un mezon virtual este
ΔE = mmezon ∙ c2
unde mmezon este masa de repaus a mezonului (nenulă).
Considerăm că mezonul se deplasează cu o viteză apropiată de cea a luminii pentru a calcula distanța parcursă de mezon în timpul său de viață Δt < h/ΔE ≈ h/m ∙ c2:

Observăm că raza de acțiune a forței nucleare tari este egală cu lungimea de undă Compton a mezonului, Λ. Dacă înlocuim masa mezonului (pionului ) cu 140 MeV obținem ≈10-15 m.
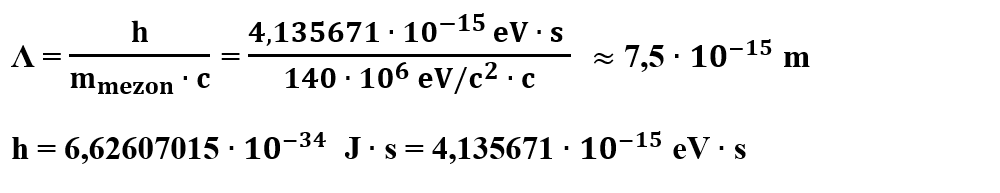
Deci, în cazul emisiei de particule virtuale cu masa nenulă de către particule reale, timpul de viață scurt al acestor particule virtuale nu le permite să se deplaseze pe distanțe mai mari de 10-15 m, chiar dacă se deplasează cu viteza luminii.