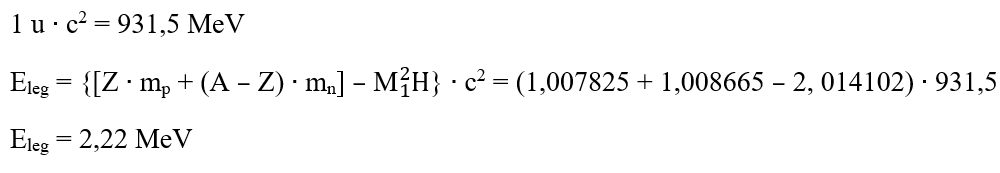V.1.4. Defect de masă. Energia de legătură a nucleului. Stabilitatea nucleului.

În studiul fizicii nucleare suntem obligați să utilizăm teoria relativității restrânse a lui Einstein. Să ne reamintim câteva noțiuni de bază ale acestei teorii.

Energia totală a unui sistem izolat (nucleu, particulă) este dată de relația lui Einstein:
E = m ∙ c²

m este masa de mișcare a sistemului (masa inerțială)
c este viteza luminii în vid

Masa inerțială a unei particule este dependentă de viteza sa.

m₀ = masa de repaus a particulei,
v = viteza particulei

Energia de repaus a sistemului izolat este:
E₀ = m₀ ∙ c²

Energia cinetică a sistemului izolat este diferența dintre energia totală și energia de repaus:
E_c = E – E₀ = (m – m₀) ∙ c²

🔦 Observație

Creșterea masei unui sistem este proporțională cu creșterea energiei sale, iar descreșterea masei unui sistem, cu descreșterea energiei sale, indiferent de procesul în care are loc variația energiei.

Absorbția energiei de către un sistem este echivalentă cu creșterea masei sale, iar eliberarea de energie, cu scăderea masei sale.

Experimental s-a descoperit că masa de repaus a nucleului atomic (M_N) este mai mică decât suma maselor de repaus a tuturor nucleonilor din care este constituit nucleul.

M_N < Z ∙ m_p + (A – Z) ∙ m_n

Z este numărul atomic
m_p este masa unui proton
A este numărul de masă
m_n este masa unui neutron

Diferența dintre suma maselor de repaus a tuturor nucleonilor din nucleu și masa de repaus a nucleului se numește defect de masă, notat cu Δm.
Δm = Z ∙ m_p + (A – Z) ∙ m_n – M_N

Energia totală a unui nucleu izolat, aflat în repaus este:
E_N = M_N ∙ c²

Energia totală a nucleonilor din nucleu, dar separați și în repaus este:
Et = [Z ∙ m_p + (A – Z) ∙ m_n] ∙ c²

Datorită defectului de masă E_t > E_N și rezultă că :
E_t – E_N = Δm ∙ c² > 0

Această relație arată că:

• la formarea nucleului din nucleonii constituenți se eliberează energie,
• desfacerea unui nucleu în repaus în nucleonii componenți, nucleul trebuie să primească energie egală cu energia eliberată la formarea lui.

E_leg = [Z ∙ m_p + (A – Z) ∙ m_n] ∙ c² – M_N ∙ c² = E_t – E_N

Energia de legătură medie pe nucleon (ε) este egală cu raportul dintre energia de legătură a nucleului respectiv (E_leg) și numărul lui de masă (A) :

Pentru ca un nucleu să fie stabil trebuie ca energia lui de legătură să fie mai mare decât zero (E_leg > 0), adică masa nucleului să fie mai mică decât masa nucleonilor componenți în repaus și izolați.

🔦 Observație

- Din E_leg > 0 și 𝛆 > 0 rezultă caracterul atractiv al forțelor nucleare tari.

- Deoarece calculul energiilor se face de obicei în megaelectronivolți (MeV) este util să cunoaștem echivalentul în energie a unității atomice de masă:
1 u ∙ c² = (931,5016 ± 0,0026) MeV

- Să ne reamintim că electronvoltul (eV) este lucru mecanic efectuat pentru a deplasa sarcina electrică elementară (e) împotriva câmpului electric generat de o diferență de potențial de 1 volt (V), adică:
L = 1 eV = 1,602 ∙ 10^-19 J

- Deoarece E_leg = ε ∙ A, putem considera că E_leg ~ A, de unde rezultă proprietatea de saturație a forțelor nucleare, adică proprietatea nucleonilor de a interacționa numai cu nucleonii vecini.

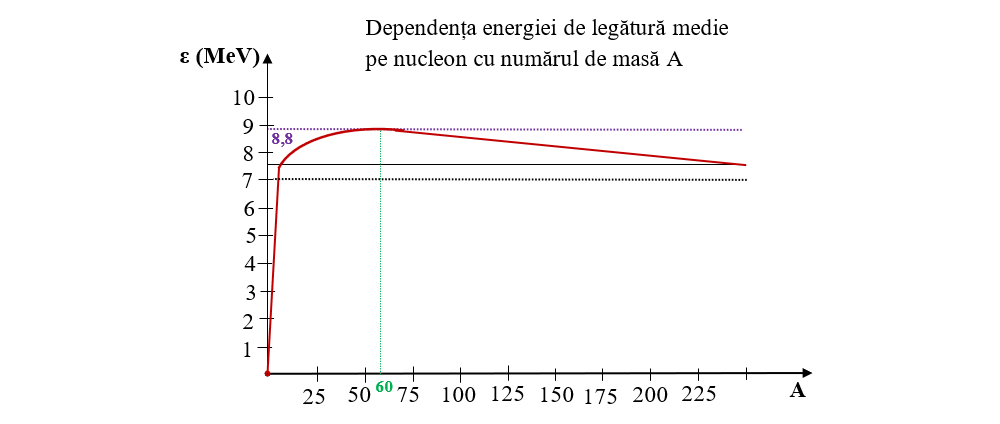
Constatări generale privind dependența energiei de legătură medie pe nucleon cu numărul de masă A:

- Nucleele cu nr. de masă A > 11 (adică 95% din atomii care există în natură) au energia de legătură medie pe nucleon cuprinsă între 7 și 8,8 MeV.

- La A = 60 (Ni) se atinge valoarea maximă de 8,8 MeV, după care scade lent, ajungând la uraniu la circa 7,5 MeV.

Concluzii privind stabilitatea unui nucleu:

Clasificarea nucleelor după stabilitatea lor:

- Nucleele ușoare cele mai stabile sunt cele care au același număr de protoni și de neutroni, adică la care Z = N.

- Nucleele grele cele mai stabile sunt cele care au numărul de protoni mai mic decât numărul de neutroni, adică Z < N și N/Z → 1,5. Pentru nucleele grele, creșterea numărului de protoni conduce la creșterea respingerii electrostatice dintre aceștia, ceea ce înseamnă pierderea stabilității lor.

🔓 Problemă rezolvată - Defect de masă. Energia de legătură a nucleului. Stabilitatea nucleului

Rezolvare:

Scriem datele problemei
Z = 1
A = 2
m_proton = 1,007825 u
m_neutron = 1,008665 u