IV.1.2. Conducția electrică în metale.
Pentru menținerea unui curent electric staționar într-un fir conductor este nevoie ca la capetele firului să menținem o diferență de potențial constantă printr-un câmp electric constant, folosind un generator electric.
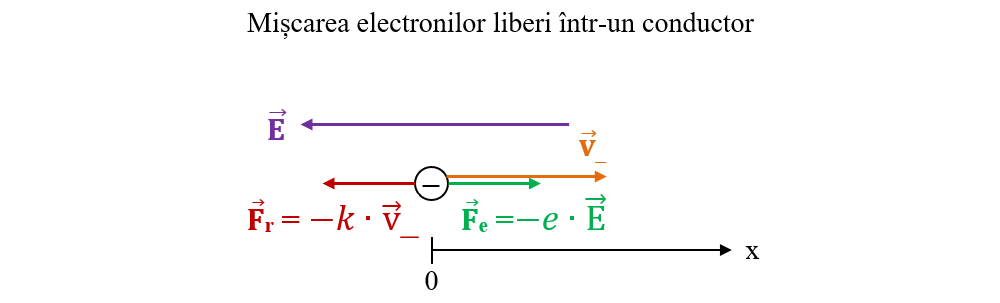
Sub acțiunea câmpului electric electronii liberi au o mișcare ordonată și accelerată.
Ei se ciocnesc de ionii rețelei cristaline pierzând din energia lor cinetică și viteza lor scade.
Câmpul electric menținut de diferența de potențial constantă îi accelerează cu o accelerație :

Pe ansamblu, electronii capătă o viteză medie constantă (notată cu v_), ceea ce înseamnă că în mișcarea lor prin conductor sunt acționați și de o forță de rezistență (Fr), proporțională cu viteza lor:

La echilibru dinamic, forța electrică (Fe) este egală în modul cu forța de rezistență (Ff) :
Fe = Fr
e ∙ E = k ∙ v_
unde:
v_ = viteză de transport (sau viteză de drift)
e = sarcina electronului
E = intensitatea câmpului electric
k = constantă de proporționalitate
🔦 Observație
Indicele minus din simbolul vitezei medii (v_) este folosit pentru a sublinia că este vorba de purtători de sarcină negativă.
Viteza de transport a electronilor liberi este proporțională cu intensitatea câmpului electric:

unde:
μ_ = mobilitatea electronilor liberi
Unitatea de măsură a mobilității este:

Considerăm o porțiune din firul conductor de lungime L și aria secțiunii normale S.
În timpul ∆t = L/v_ toți N electroni liberi vor trece prin secțiunea S.
Sarcina transportată prin secțiunea S în intervalul de timp ∆t este:
Q = N ∙ e
Intensitatea curentului electric este :

Notăm cu n- concentrația de electroni liberi, care reprezintă numărul de electroni liberi din unitatea de volum V.
Numărul de electroni liberi (N) din volumul V = S ∙ L în funcție de concentrația electronilor liberi este :
N = n- ∙ V = n- ∙ S ∙ L
Astfel, intensitatea curentului electric devine :
I = n- ∙ S ∙ e ∙ v-
Notăm cu j densitatea de curent, dată de raportul dintre intensitatea curentului și aria secțiunii transversale:

🔦 Observație

Dacă notăm conductivitatea cu σ = n- ∙ e ∙ μ-, obținem forma locală a legii lui Ohm, valabilă în fiecare punct al secțiunii transversale considerate:

Știind că rezistivitatea ρ este inversul conductivității, obținem pentru vectorul densitate de curent:
