II.5. Lentile. Asociații de lentile.

• II.5.1. Tipuri de lentile.
• II.5.2. Formarea imaginii unui obiect în lentile.
• II.5.3. Formulele lentilelor subțiri.
• II.5.4. Asociații de lentile.

II.5.1. Tipuri de lentile.

Lentilele sunt corpuri transparente care au cel puțin o suprafață sferică.

Elementele unei lentile :

Axa optică principală care se trasează prin mijlocul lentilei.

Centrul optic al lentilei (O) aflat la intersecția lentilei cu axa optică principală.

Două focare așezate de-o parte și de alta față de centrul optic al lentilei, la distanțe egale.

• Focarul aflat în partea stângă față de O se numește focar negativ / obiect (F₁), deoarece se află pe axa numerelor negative.

• Focarul aflat în partea dreaptă față de O se numește focar pozitiv / imagine (F₂), deoarece se află pe axa numerelor pozitive.

Centrele de curbură (C₁ și C₂) ale dioptrilor care mărginesc lentila aflate de-o parte și de alta față de O, la o distanță dublă față de OF.

🔦 Observații

Dacă grosimea lentilei este mică în comparaţie cu razele de curbură ale feţelor, lentila este considerată subţire.

Distanța OF₁ = OF₂ = f = distanță focală

În construcția imaginii unui obiect într-o lentilă vom desena numai centrul de curbură aflat în partea stângă față de O, la o distanță egală cu dublul distanței focale, OC = 2f.

Clasificarea lentilelor:

1. Lentile convergente (convexe) sunt lentilele care transformă un fascicul de lumină paralel într-un fascicul convergent. Ele refractă lumina prin focarul pozitiv și de aceea se mai numesc și lentile pozitive. Ele măresc scrisul. Sunt mai groase la mijloc și mai subțiri la capete.

👀 Experiment: Lentila convergentă
🔥 Atenție! Nu îndrepta lumina laserului spre ochi!

2. Lentile divergente (concave) sunt lentilele care transformă un fascicul de lumină paralel într-un fascicul divergent. Ele refractă lumina prin focarul negativ și de aceea se mai numesc și lentile negative. Ele micșorează scrisul. Sunt mai groase la capete și mai subțiri la mijloc.

👀 Experiment: Lentila divergentă
🔥 Atenție! Nu îndrepta lumina laserului spre ochi!

II.5.2. Formarea imaginii unui obiect în lentile.

Pentru a forma imaginea unui obiect într-o lentilă convergentă trebuie să trasăm două raze:

• Desenăm simbolul lentilei convergente.

• Trasăm prin mijlocul ei axa optică principală.

• Punem elementele lentilei (O, F₁, F₂, C).

• Desenăm obiectul (AB) în fața lentilei (în partea stângă), printr-un segment cu săgeată.

• Trasăm o rază care pleacă din vârful obiectului (B) paralelă cu axa optică până întâlnește lentila și apoi o ducem prin focarul pozitiv (F₂), deoarece lentila convergentă refractă lumina prin focarul pozitiv.

• Trasăm a doua rază din vârful obiectului care să treacă prin centrul optic al lentilei (O). Prelungim aceste raze până se intersectează. La intersecția lor punem B' care este vârful imaginii (im) obiectului (ob) AB.

• Din B' trasăm o perpendiculară pe axa optică, piciorul acesteia îl notăm cu A' și reprezintă baza im A'B'.

• Punem vârful săgeții în B' și așa obținem imaginea obiectului AB în lentila convergentă.

În funcție de distanța obiectului față de lentilă, avem trei tipuri de imagini în lentila convergentă.

I. Când obiectul este situat în intervalul (-∞) și C, imaginea obiectului are următoarele caracteristici :

• Mai mică decât obiectul AB.

• Răsturnată

• Reală (se formează la intersecția razelor refractate, poate fi proiectată pe un ecran).

🔦 Observație
La lentile, care sunt aplicații ale refracției luminii, razele care ies din lentilă sunt razele refractate.
Razele care le desenăm în fața lentilei sunt prelungirile razelor refractate.

II. Când obiectul este situat în intervalul C și F₁, imaginea obiectului are următoarele caracteristici:

• Mai mare decât obiectul AB.

• Răsturnată

• Reală (se formează la intersecția razelor refractate, poate fi proiectată pe un ecran).

III. Când obiectul este situat în intervalul F₁ și O, imaginea obiectului are următoarele caracteristici:

• Mai mare decât obiectul.

• Dreaptă

• Virtuală (se formează la intersecția prelungirilor razelor refractate, nu poate fi proiectată pe un ecran).

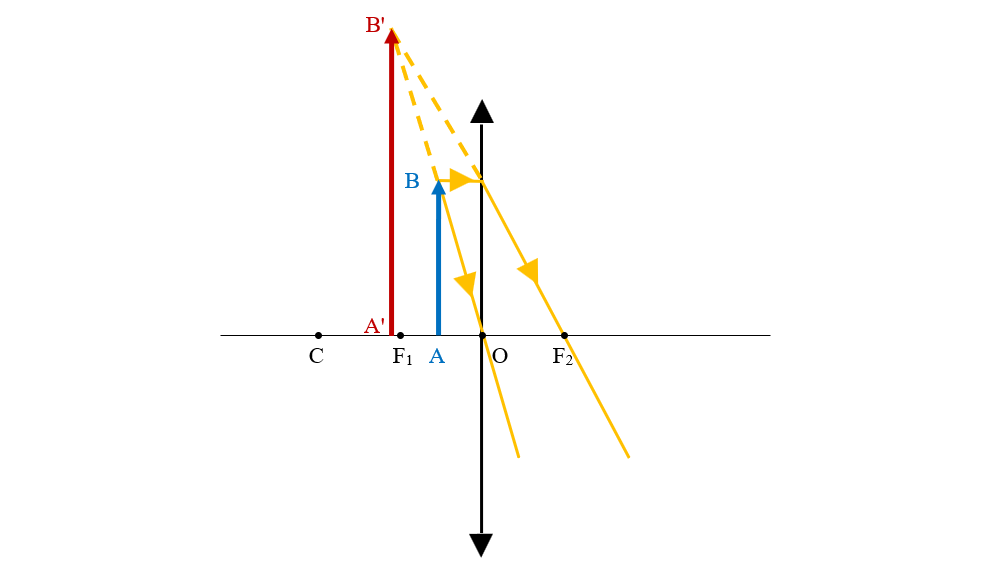
🔦 Observații importante
Când obiectul AB este situat chiar în C, im ob A'B' este egală ca mărime cu obiectul.
Când obiectul AB este situat chiar în F₁, im ob A'B' nu se poate forma deoarece razele ies din lentila convergentă paralele și nu se intersectează.

👀 Experiment: Formarea imaginilor în lentila convergentă.
🔥 Atenție! Acest experiment se efectuează numai în prezența unui adult!
🔥 Atenție! Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi!

Materiale necesare:
Lentilă convergentă (lupă), lumânare, chibrit.

Modul de lucru:

• Așază lumânarea aprinsă la o distanță de 40-60 cm față de un perete.
• Mută, încetul cu încetul, lupa dinspre lumânare spre perete, astfel încât vârful lumânării, mijlocul lentilei să fie pe aceeaşi dreaptă.
• Când lupa este aproape de flacăra lumânării se formează o imagine virtuală, mai mare decât flacăra și dreaptă pe care o poți vedea prin lupă.
• Depărtează lupa de flacără până când pe perete se formează imaginea clară a lumânării mai mare, reală și răsturnată.
• Depărtează și mai mult lupa de flacără până când pe perete se formează o imaginea clară a lumânării mai mică, reală și răsturnată.

  În lentila convergentă (lupă) se formează trei tipuri de imagini ale obiectelor.

Pentru a forma imaginea unui obiect într-o lentilă divergentă trebuie să trasăm două raze:

• Desenăm simbolul lentilei divergente.

• Trasăm prin mijlocul ei axa optică principală.

• Punem elementele lentilei (O, F₁, F₂, C).

• Desenăm obiectul (AB) în fața lentilei (în partea stângă) printr-un segment cu săgeată.

• Trasăm o rază care pleacă din vârful obiectului (B) paralelă cu axa optică până întâlnește lentila și apoi o ducem prin focarul negativ (F₁), deoarece lentila divergentă refractă lumina prin focarul negativ.

• Trasăm a doua rază din vârful obiectului care să treacă prin centrul optic al lentilei (O). Prelungim aceste raze până se intersectează. La intersecția lor punem B' care este vârful imaginii (im) obiectului (ob) AB.

• Din B' trasăm o perpendiculară pe axa optică, piciorul acesteia îl notăm cu A' și reprezintă baza im A'B'.

• Punem vârful săgeții în B' și așa obținem imaginea obiectului AB în lentila convergentă.

În lentila divergentă obținem o imagine care are aceleași caracteristici indiferent de distanța obiectului față de lentilă:

• Mai mică decât obiectul.

• Dreaptă

• Virtuală (se formează la intersecția prelungirilor razelor refractate, nu poate fi proiectată pe un ecran).

👀 Experiment: Formarea imaginilor în lentila divergentă.
🔥 Atenție! Acest experiment se efectuează numai în prezența unui adult!
🔥 Atenție! Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi!

Materiale necesare:
Lentilă divergentă (ochelari pentru miopie cu dioptrii negative), lumânare, chibrit.

Modul de lucru:

• Așază lumânarea aprinsă la o distanță de 40-60 cm față de un perete.
• Mută, încetul cu încetul, lentila divergentă dinspre lumânare spre perete, astfel încât vârful lumânării, mijlocul lentilei să fie pe aceeaşi dreaptă.
• Când lentila este aproape de flacăra lumânării se formează o imagine virtuală, mai mică decât flacăra și dreaptă pe care o poți vedea prin lentilă.
• Depărtează lentila de flacără și vei vedea, tot privind prin lentilă, imaginea clară a lumânării mai mică, virtuală și dreaptă.
• Depărtează și mai mult lentila de flacără și vei vedea aceeași imagine din ce în ce mai mică decât flacăra, dar cu aceleași caracteristici.

  În lentila divergentă se formează un singur tip de imagine ale obiectelor, indiferent de distanța dintre obiect și lentilă.

II.5.3. Formulele lentilelor subțiri.

Convenții de semne:

• x₁ = distanța de la obiectul AB la lentilă care se ia tot timpul negativă deoarece este pe axa numerelor negative.

• x₂ = distanța de la imaginea A'B' la lentilă care se ia pozitivă când imaginea este reală (se formează în spatele lentilei, pe axa numerelor pozitive) și negativ când imaginea este virtuală (se formează în fața lentilei, pe axa numerelor negative).

• y₁ = înălțimea obiectului AB care se ia pozitivă dacă obiectul este deasupra axei optice principale și negativă dacă obiectul este sub axa optică principală.

• y₂ = înălțimea imaginii A'B' se ia pozitivă când imaginea este dreaptă (deasupra axei optice principale) sau negativă când imaginea este răsturnată (sub axa optică principală).

• Distanța focală se consideră pozitivă (f > 0) pentru lentilele convergente și negativă (f < 0) pentru lentilele divergente.

Formula fundamentală a lentilelor subțiri:

x₁ = distanța de la obiectul AB la lentilă

x₂ = distanța de la imaginea A'B' la lentilă

f = distanța focală a lentilei

🔦 Observație

Din această formulă putem afla distanța de la imagine la lentilă:

Mărirea liniară transversală (β) este o mărime fizică adimensională egală cu raportul dintre înălțimea imaginii și înălțimea obiectului.

x₁ = distanța de la obiectul AB la lentilă

x₂ = distanța de la imaginea A'B' la lentilă

y₁ = înălțimea obiectului AB

y₂ = înălțimea imaginii A'B'

Convergența unei lentile (C) este o mărime fizică egală cu inversul distanței focale (f).

🔦 Observații

Dacă β > 0, imaginea este dreaptă.

Dacă β < 0, imaginea este răsturnată.

Dacă |β| > 1, imaginea este mărită.

Dacă |β| < 1, imaginea este micșorată.

👀 Experiment: Calcularea distanței focale a unei lentile.
🔥 Atenție! Acest experiment se efectuează numai în prezența unui adult!
🔥 Atenție! Când lucrezi cu surse de foc ai grijă să ai părul strâns și să nu porți haine cu mâneci largi!

🔓 Problemă rezolvată

1. În fața unei lentile convergente cu distanța focală de 20 cm se așază o lumânare la o distanță de 60 cm.

Se cere:

a) Desenează formarea imaginii lumânării în această lentilă.

b) Calculează coordonata (distanța) la care trebuie așezat un ecran pe care să se formeze imaginea clară a lumânării.

c) De câte ori este mărită/micșorată imaginea? Caracterizează imaginea lumânării.

d) Câte dioptrii are această lentilă?

Rezolvare:

Notăm datele problemei:
f = 20 cm (distanța focală a lentilei se ia pozitivă, întrucât lentila este convergentă și refractă lumina prin focarul pozitiv)
x₁ = - 60 cm (distanța de la obiectul AB la lentilă se ia negativă, întrucât este pe axa numerelor întregi negativă)
x₂ = distanța de la imaginea A'B' la lentilă = ?
β = ?
C = ?

a)

b) Scriem formula fundamentală a lentilelor subțiri:

c)

Valoarea negativă a măririi liniare transversale arată că imaginea este răsturnată, iar faptul că este subunitară arată că imaginea este mai mică decât obiectul.

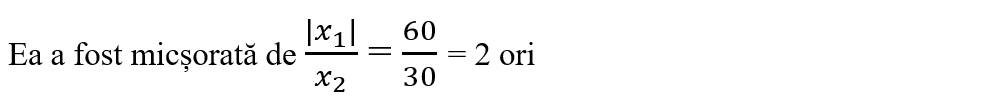
Imaginea este reală (formată în spatele lentilei,deoarece x₂ este pozitivă).

d) Calculăm convergența lentilei:

II.5.4. Asociații de lentile.

Un sistem format din două sau mai multe lentile care au aceeași axă optică principală se numește asociație de lentile.

Imaginea formată de prima lentilă devine obiect pentru lentila următoare și așa mai departe până la ultima lentilă care va da imaginea finală.

I. Cel mai utilizat sistem este cel cu lentile alipite (acolate) în care distanța (d) dintre lentile este zero, având același centru optic și focarul imagine (F₂) al primei lentile (L) coincide cu focarul obiect (F'₂).

Pentru un astfel de sistem format din k lentile avem:

1. Inversul distanței focale a sistemului de lentile (F) este egal cu suma inverselor distanțelor focale a lentilelor asociației:

2. Convergența sistemului (C) este egală cu suma convergențelor lentilelor componente:

C = C₁ + C₂ +...+ C_k

3. Mărirea liniară transversală a sistemului (β) este egală cu produsul măririlor transversale a lentilelor componente:

β = β₁ ∙ β₂ ∙… β_k

Dacă notăm cu x'₂ distanța de la imaginea finală la lentila a doua L₂ și cu x₁ distanța de la obiect la prima lentilă L₁, avem relația :

II. Un alt sistem de lentile este sistemul telescopic care este un sistem afocal, în care fasciculul de ieșire (emergent), provenit dintr-un fascicul paralel, este tot paralel. Focarul imagine al primei lentile (F₂) coincide cu focarul obiect al celei de-a doua lentilă (F'₁).

1. Distanța dintre lentile este:

d = f₁ + f₂

2. Mărirea liniară transversală este:

🔦 Observație

Sistemul telescopic nu poate avea în componență doar lentile divergente și imaginea este răsturnată atunci când are în componență doar lentile convergente.

Pentru a afla poziția (x'₁) a imaginii intermediare față de prima lentilă (L₁) și dimensiunea imaginii formată de prima lentilă, aplicăm formula punctelor conjugate pentru L₁:

Știind distanța dintre lentile putem calcula poziția imaginii intermediare (formată de L₁) față de lentila L₂:

d = x'₁ + (- x₂)

x2 = x'₁ - d

Pentru a afla poziția (x'₂) a imaginii finale față de a doua lentilă (L₂) și dimensiunea imaginii formată de a doua lentilă, aplicăm formula punctelor conjugate pentru L₂:

🔦 Observație

Mărirea liniară transversală pentru un sistem telescopic are aceeași formulă și pentru un sistem format dintr-o lentilă convergentă cu una divergentă.

🔐 Aplicații

Sistemele de lentile afocale sunt folosite în construcția teleobiectivelor aparatelor foto și la telescoape.