III.4. Mărimi caracteristice curentului alternativ.

Variația t.e.m. induse este sinusoidală și curentul alternativ obținut este un curent alternativ sinusoidal. T.e.m. e și intensitatea curentului alternativ trec prin aceleași valori și în același sens la intervale egale de timp.

Curentul alternativ fiind periodic este caracterizat de mărimile:

• Perioada (T) este intervalul de timp după care tensiunea și intensitatea curentului alternativ trec prin aceleași valori și în același sens, adică efectuează o oscilație completă (sinusoidă).

Unitatea de măsură pentru perioadă în SI este:

[T]_SI = s (secunda)

• Frecvența (ν) arată numărul de oscilații complete efectuate în unitatea de timp, fiind inversul perioadei:

Unitatea de măsură pentru frecvență în SI este:

[ν]_SI = Hz (hertz)

Tipuri de curenți alternativi după frecvența lor

• Amplitudinea este valoarea maximă pe care o au tensiunea și intensitatea curentului alternativ în timpul unei perioade, notate E_m, U_m și I_m.

E_m este valoarea maximă a t.e.m. induse

E_m = ω ∙ Φ_m este valoarea maximă a t.e.m. induse

I_m este valoarea maximă a intensității curentului alternativ

• Valoarea instantanee este valoarea pe care o au tensiunea sau intensitatea curentului alternativ la un moment oarecare de timp:

e = E_m ∙ sin ωt

i = I_m ∙ sin ωt

• Pulsația (ω) reprezintă numărul de perioade în 2π unități de timp:

Unitatea de măsură pentru pulsație în SI este:

[ω]_SI = rad/s (radian/secundă)

• Faza (ϕ) a intensității și tensiunii alternative este argumentul sinusului din expresia intensității, respectiv tensiunii instantanee:

ϕ = ωt + φ

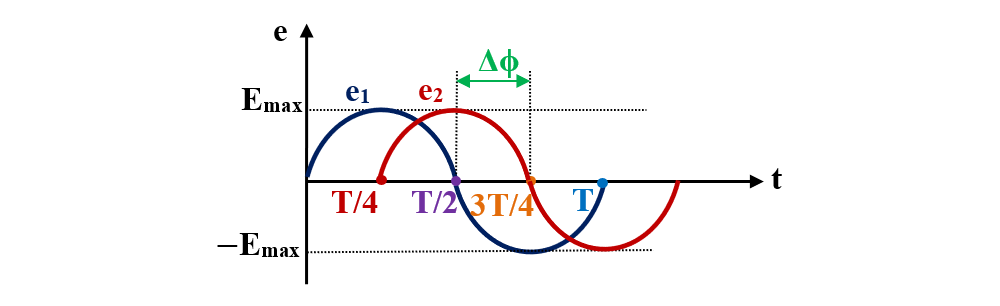
Dacă planele a două spire rotitoare identice 1 și 2, așezate coaxial, fac la momentul inițial t = 0, cu un plan de referință, unghiurile φ₁, respectiv φ₂, prin rotirea lor uniformă cu viteza unghiulară ω, în sens antiorar, în fiecare spiră se va genera câte o t.e.m. sinusoidală

e₁ = E_m ∙ sin (ωt + φ₁)

e₂ = Em ∙ sin (ωt + φ₂)

Aceste tensiuni au aceeași valoare maximă, aceeași perioadă, dar se deosebesc prin fază, fiind defazate una față de alta cu:

Δϕ = ϕ₁ - ϕ₂ = ωt + φ₁ - ωt - φ₂ = φ₁ - φ₂

Δϕ = φ₁ - φ₂ se numește diferență de fază sau defazaj.

Reprezentarea mărimilor caracteristice curentului alternativ

Tensiunea și intensitatea curentului alternativ sinusoidal pot fi reprezentate:

1. Analitic, prin formulele ce exprimă valorile instantanee:

e = E_m ∙ sin ωt

i = I_m ∙ sin ωt

2. Grafic prin sinusoide:

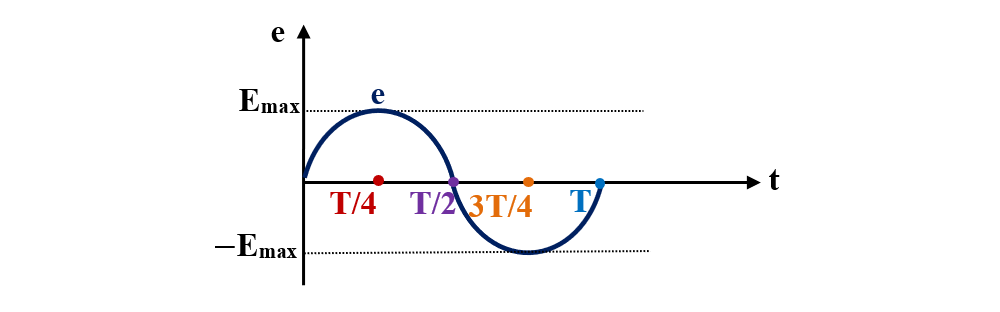
3. Fazorial prin diagrame Fresnel în care fiecărei mărimi sinusoidale i se asociază un fazor (vector rotitor) care are modulul egal cu amplitudinea mărimii, iar unghiul pe care îl face cu axa Ox este egal cu faza mărimii la momentul respectiv, fiind pozitiv pentru sensul trigonometric (sensul pozitiv este cel invers acelor de ceas).

🔦 Observații importante:

Energia mecanică necesară rotirii uniforme a cadrului sau a bobinei în câmp magnetic se transformă în energie a curentului electric alternativ sinusoidal. Factorul excitator este fluxul de inducție magnetică cu variație cosinusoidală prin suprafața delimitată a cadrului Φ_c = B ∙ S ∙ cos ωt sau prin spirele bobinei Φ_b = N ∙ B ∙ S ∙ cos ωt, unde N este numărul de spire și S este aria unei spire.

Datorită variației fluxului magnetic: Φ = Φ_m ∙ cos ωt, prin spiră se produce fenomenul de inducție electromagnetică cu apariția unei tensiuni electromotoare e cu expresia:

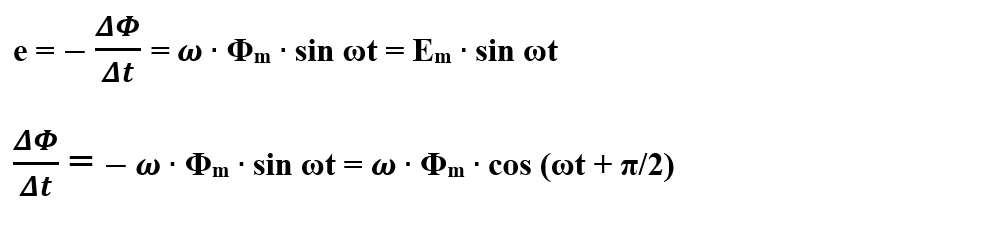
Comparăm următoarele două expresii:

Diferența dintre faza mărimii oscilatorii armonice și faza vitezei ei de variație este:
φ = ωt – (ωt + π/2) = – π/2

Diferența dintre faza vitezei de variație a mărimii oscilatorii armonice și faza mărimii oscilatorii armonice este:
φ = ωt + π/2 – ωt = π/2

🔓 Problemă rezolvată:

1. O bobină cadru dreptunghiulară cu 100 de spire și aria secțiunii de 20 cm², se rotește în sens trigonometric într-un câmp magnetic uniform de inducție 0,05 T. Știind că rotația cadrului are o turație de 3600 rot/min în jurul unei axe perprndiculare pe direcția câmpului calculează frecvența t.e.m. induse în bobină și expresia valorii instantanee a acestei tensiuni. Consideră ca origine a timpului momentul când normala la suprafața spirei face un unghi αʹ = π/4 cu vectorul inducției magnetice.

Rezolvare:

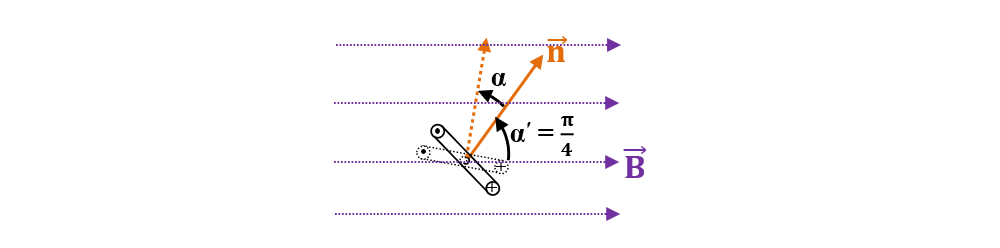
Scriem datele problemei:
N = 100 spire
S = 20 cm² = 0,002 m²
B = 0,05 T
n = 3600 rot/min
αʹ = π/4

Frecvența t.e.m. induse este:

T.e.m.indusă în bobină este: