II.11.2. Rezistența adițională a voltmetrului.

Pentru a mări domeniul de măsurare de n ori al unui voltmetru cu rezistența proprie R_V și care poate măsura o tensiune maximă U_V, se conectează în serie cu acesta o rezistență adițională cu rezistența R_a.

Calibrele voltmetrului depind de rezistența adițională.

Tensiunea maximă care poate fi măsurată este:
U = n ∙ U_V = U_V + U_a
n ∙ U_V = U_V + U_a
U_a = (n – 1) ∙ U_V

Pentru a afla rezistența adițională împărțim ultima expresie cu I_V:

În funcție de valoarea rezistenței adiționale, voltmetrele au calibre diferite.

🔓 Problemă rezolvată

5. O sursă electrică cu t.e.m. de 12 V are o rezistență internă de 0,5 Ω. Ea este legată la un bec cu rezistența de 10 Ω. Se cere:
a) Cât este intensitatea curentului ce trece prin bec dacă rezistența ampermetrului este de 0,001 Ω (considerăm că nu este un ampermetru ideal care are rezistența zero)?
b) Cât este intensitatea măsurată de ampermetru dacă scoatem becul din circuit ?
c) Cât este intensitatea curentului dacă la bornele becului legăm un voltmetru care nu este ideal, având o rezistență de 100000 Ω (voltmetrul ideal are rezistența care tinde spre infinit, pentru a nu permite trecerea curentului prin acesta și astfel se obține citirea corectă) ?
d) Dacă legăm direct voltmetrul la bornele sursei, cât este intensitatea curentului ?

Rezolvare:

Scriem datele problemei:
E = 12 V
r = 0,5 Ω
R_b = 10Ω
R_A = 0,001 Ω
R_V = 100000 Ω

a)

Becul și rezistorul ampermetrului și rezistența sursei sunt în serie și au rezistența echivalentă:

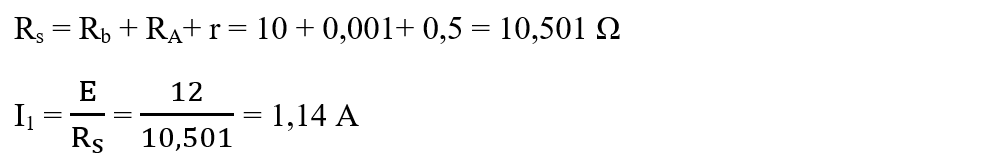
b)

Dacă ampermetrul ar fi fost unul ideal, cu rezistența 0, el ar fi scurtcircuitat sursa și ar fi măsurat curentul de scurtcircuit cu formula

Însă acest ampermetru nu are rezistența 0 și vom avea o intensitate:

c)

R_b și R_V sunt în paralel și le calculăm rezistența echivalentă R_p:

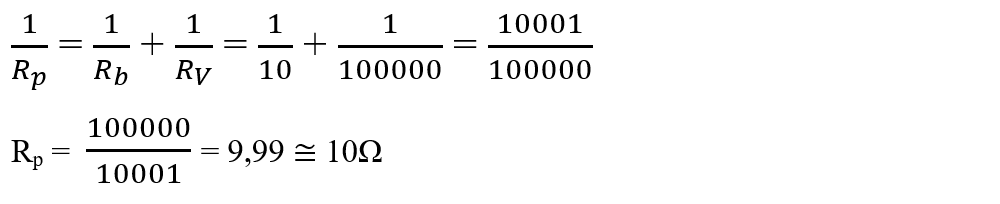
R_p, R_A și r sunt în serie și au rezistența echivalentă:

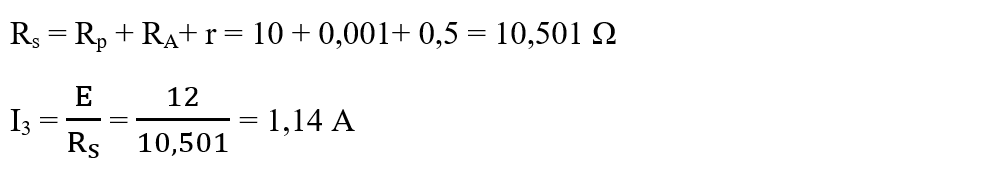
d)

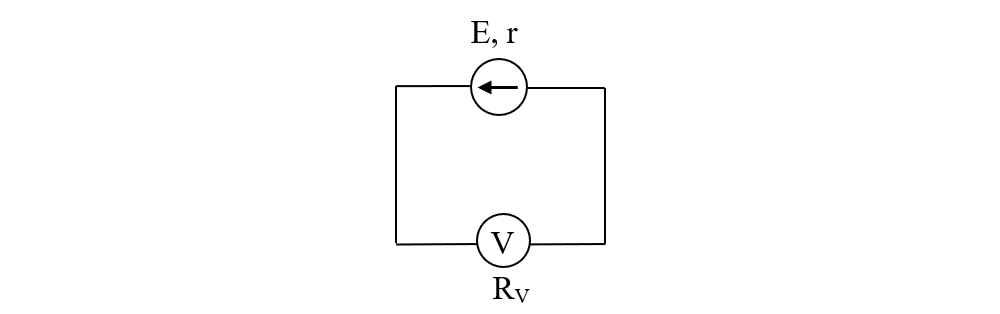
Legând direct voltmetrul la sursă, r și R_V vor fi în serie și intensitatea va deveni:

Dacă voltmetru ar fi fost unul ideal (cu rezistența infinită), intensitatea curentului ar fi fost zero.